[剑指offer]重建二叉树

Posted 2022-01-27 一个正直的男孩

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[剑指offer]重建二叉树相关的知识，希望对你有一定的参考价值。

文章目录

第一层二叉树遍历
第二层给定前中序构建一个二叉树
唠唠家常

第一层二叉树遍历

题目介绍

给定一个（前序遍历）字符串，构建二叉树，并且以中序打印，#==nullpet , ’ ‘==空树

如果忘记请看这篇博客----->回顾二叉树概念

思路

前序是先根遍历，在左子树，右子树
分别对树的左右区间进行构造
根据# 进行构建树那么就会一下俩种情况

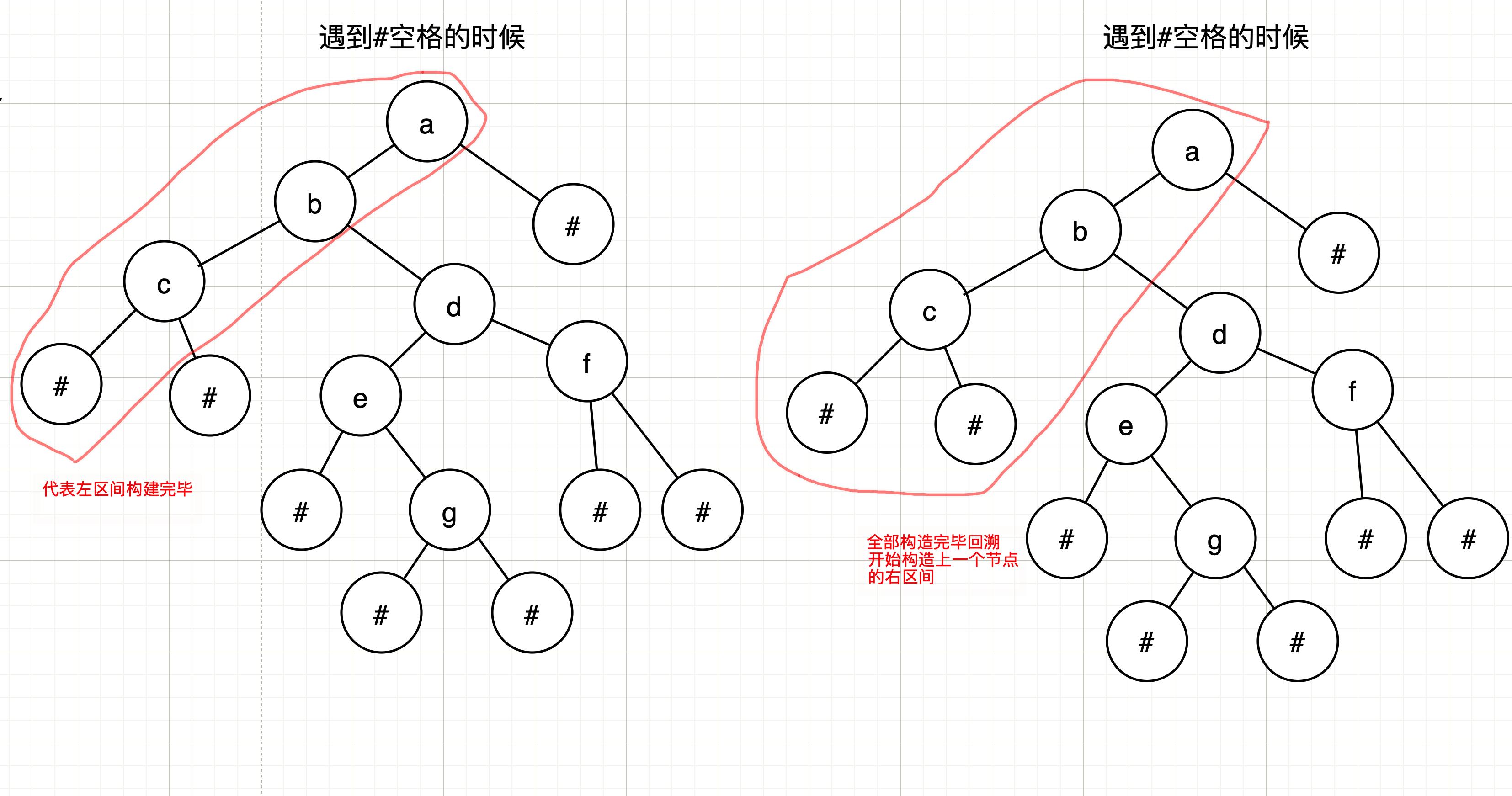
碰到一个#就说明当前的构建的区间已经全部构建完毕，已经没有元素可以构造了（类似中序遍历一直走到叶子节点）
而碰到##就代表遇到的是叶子节点代表左右区间都构建完成(后续遍历一直走到根节点)

代码：

#include<iostream>
using namespace std;
struct TreeNode 

      char val;
      TreeNode *left;
      TreeNode *right;
      TreeNode(char x) : val(x), left(NULL), right(NULL) 
  ;

TreeNode*Construction(string &d1,int& i)

    if(d1[i]=='#')//半边子树已经构建完成
    
        return nullptr;
    
    TreeNode *root=new TreeNode(d1[i]);//构造节点
    
    root->left=Construction(d1,++i);//构造左子树
    root->right=Construction(d1,++i);//构造右子树
    
    return root;

  void Print(TreeNode * d1)//打印
  
      if(d1==nullptr)
          return;
      Print(d1->left);
      cout<<d1->val<<' ';
       Print(d1->right);
  
int main()

    string d1;
    cin>>d1;
    int i=0;
  Print(Construction(d1,i));

图解构建：

其实思路非常的简单但是他是如何构建的呢？老样子画图
蓝线代表：递归
橘线代表：回到调用位置
绿线代表：回到调用位置（节点构建完毕）

后面的节点构建也是如此

第二层给定前中序构建一个二叉树

题目描述：

简单回顾：

前序遍历是先根在左子树右子树
中序遍历是先左子树在根右子树

思路：

前序每次都先根遍历，那么就可以依靠前序来确定根节点的位置，而中序遍历是先左子树在根，那么我们就可以中序中找前序确定好的根来划分左右子树，思路其实就俩句话，前序找根，中序划分左右子树

代码：

第一步：
进行特殊处理,构建子函数进行递归构建树(原来的函数结构不满足递归构树的要求)

 TreeNode* reConstructBinaryTreeHelp(vector<int>& pre,int pre_start,int pre_end,vector<int>& vin,int vin_start,int vin_end)
    
    
    
    TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin)
    
        if(pre.size()<vin.size())//特殊情况给你的序列不属于同一树
        
            return nullptr;
        
        
    
       
     return reConstructBinaryTreeHelp(pre,0,pre.size()-1,vin,0,pre.size()-1);//构建树,传pre和vin的有效区间，也可以看出我们传的是闭区间，就是【0,pre.size()-1】使用下标都可以访问到，vin也一样

第二步实现递归主逻辑：

 TreeNode* reConstructBinaryTreeHelp(vector<int>& pre,int pre_start,int pre_end,vector<int>& vin,int vin_start,int vin_end)
    
    
    
      //递归结束出口
        if(pre_start>pre_end||vin_start>vin_end)//如果他们的起始位置都大于他们的结束位置也就说明没有节点了
        
            return nullptr;
        
       TreeNode*root=new TreeNode(pre[pre_start]);//构造节点，前序是根
    
    
      for(int i=vin_start;i<=vin_end;i++)//在中序中划分左右区间，那么起始位置肯定是中序的的start末尾就是end
      
          if(pre[pre_start]==vin[i])//中序找到根划分左右子树，并开始构建
          
              //构建左子树，把控区间
              root->left=reConstructBinaryTreeHelp(pre, , ,vin, , );
              root->right=reConstructBinaryTreeHelp(pre, , ,vin, , );
              break;//走到这一步说明了树已经构建完毕
          
          
      
      return 0;

第三步确定区间：

其实这一块难的不是思路，思路很好想，但是把控他的区间却是这一到题的精髓，所以我们把他一一拎出来详细分析,这里还需要结合第二部划分左右子树循环这一块的代码，但是我会画图标明

第一次划分

左子树的：

pre_start

在第一次划分可以看出，pre_start其实就只需要指向下一个位置就可以了，前序是确定根的

vin_start

他的区间依旧是vin_start如第一次划分中所示

vin_end

end的位置就是当前root的前一个位置(i-1)，那么root所在的位置就是 i(第二部分确定root位置的循环)，且代码实现是一个闭区间,如第一次划分所示

pre_end

那么现在我们来想一个问题我们这么知道前序中左子树的节点个数？

根据图中所示前序的节点区间是[1，7]，那么如何控制呢？那我们现在在想一想有啥和左子树节点密切相关的东西…………，哦中序遍历的start 与 end 不就指向区间不就是左子树的节点个数吗？对的

如上面分析得出vin_end==i-1，那么最终可以得出区间就是 pre_start+1（前序的起始位置） +i-1 -vin_start----> 最终得到的区间就是 pre_start+i-vin_start

右子树的：

pre_start

由图可以看出，右子树对于前序来说其实就上左子树pre_end+1 也就是 pre_start+i-vin_start+1

pre_end

他的结束位置也很简单如图所示，依旧还是pre_end

vin_start

从图中可以看出被分割后右子树的区间起始位置就是 i（root节点）后面也就是 i+1

vin_end

他的结束位置也很简单如图所示，依旧还是vin_end

代码：

     root->left= reConstructBinaryTreeHelp(pre,pre_start+1,  pre_start+i-vin_start       ,vin,vin_start ,i-1);
                root->right=reConstructBinaryTreeHelp(pre,  pre_start+i-vin_start+1           , pre_end,vin,i+1 , vin_end);