频率响应是啥

Posted 2023-05-02

不需要单纯的概念解释、 举例说明

频率响应是指将一个以恒电压输出的音频信号与系统相连接时，音箱产生的声压随频率的变化而发生增大或衰减、相位随频率而发生变化的现象，这种声压和相位与频率的相关联的变化关系称为频率响应。

在额定的频率范围内，输出电压幅度的最大值与最小值之比，以分贝数（dB）来表示其不均匀度。频率响应在电能质量概念中通常是指系统或计量传感器的阻抗随频率的变化。

根据频率响应可以比较直观地评价系统复现信号的能力和过滤噪声的特性。在控制理论中，根据频率响应可以比较方便地分析系统的稳定性和其他运动特性。

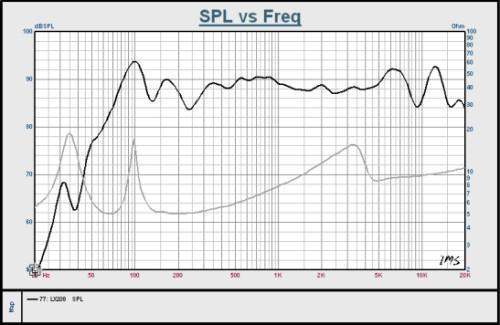
扩展资料

频率响应确定方法：

1、分析法

基于物理机理的理论计算方法，只适用于系统结构组成易于确定的情况。在系统的结构组成给定后，运用相应的物理定律，通过推导和计算即可定出系统的频率响应。分析的正确程度取决于对系统结构了解的精确程度。

2、实验法

采用仪表直接量测的方法，可用于系统结构难以确定的情况。

常用的实验方式是以正弦信号作为试验信号，在所考察的频率范围内选择若干个频率值，分别测量各个频率下输入和稳态输出正弦信号的振幅和相角值。输出与输入的振幅比值随频率的变化特性是幅频特性，输出与输入的相角差值随频率的变化特性是相频特性。

参考技术A

频率响应是指将一个以恒电压输出的音频信号与系统相连接时，音箱产生的声压随频率的变化而发生增大或衰减、相位随频率而发生变化的现象，这种声压和相位与频率的相关联的变化关系称为频率响应。

也是指在振幅允许的范围内音响系统能够重放的频率范围，以及在此范围内信号的变化量称为频率响应，也叫频率特性。在额定的频率范围内，输出电压幅度的最大值与最小值之比，以分贝数（dB）来表示其不均匀度。频率响应在电能质量概念中通常是指系统或计量传感器的阻抗随频率的变化。

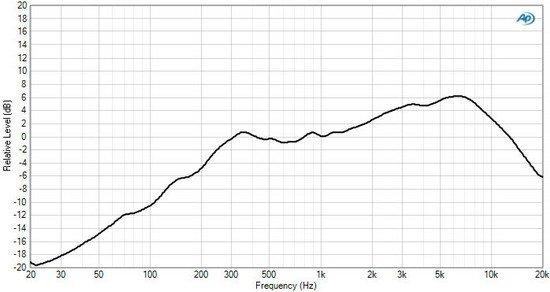
扩展资料：

系统对正弦信号的稳态响应特性。稳态是系统的运动在过渡过程结束后的状态。系统的频率响应由幅频特性和相频特性组成。幅频特性表示增益的增减同信号频率的关系；相频特性表示不同信号频率下的相位畸变关系。根据频率响应可以比较直观地评价系统复现信号的能力和过滤噪声的特性。在控制理论中，根据频率响应可以比较方便地分析系统的稳定性和其他运动特性。频率响应的概念在系统设计中也很重要。

参考资料来源：百度百科-频率响应

参考资料来源：百度百科-频率特性

参考技术B 我从音乐的角度通俗的说一说吧
就是音响系统对输入信号的反应和辨别能力。
比如一台好的音响，他的频率响应范围是20赫兹到20000赫兹。那么当一个包含有20-20000赫兹的音频信号的音乐进来之后，它就会有足够深的低频下潜和非常出色的高频表现；假如你把这个信号输入给一台比较烂的音响（我们假设它只有100-12000的频率响应范围），那么比这个范围低或者高的信号音响就无法处理和播放，你就会感觉这个音乐很窄，缺乏表现力。
当然频率响应还有一些别的必须要参考的标准，比如在某个频段，响应的情况如何，这里略过。
我们经常会在录音机或者播放器上看到一些上下跳动的曲线（或者并排的小长条）这个其实就是频响曲线了。本回答被提问者采纳

频率为随机变量的正弦曲线 - FFT 脉冲是啥样的？

【中文标题】频率为随机变量的正弦曲线 - FFT 脉冲是啥样的？

【英文标题】：Sinusoids with frequencies that are random variales - What does the FFT impulse look like?频率为随机变量的正弦曲线 - FFT 脉冲是什么样的？

【发布时间】：2016-04-16 15:59:03

【问题描述】：

我目前正在使用 C++ 编写一个程序，在该程序中我正在计算 wav 文件的时变 FFT。我有一个关于绘制 FFT 的结果的问题。

例如，我有一个 70 Hz 的信号，它是由某些具有某些谐波的仪器产生的。尽管我说这个信号是 70 Hz，但它是一个真实的信号，我假设 70 Hz 信号会有一些随机性变化。假设我以 20kHz 的采样率对其采样 1 秒。我意识到采样周期可能不需要 1 秒，但请耐心等待。

因为我现在有 20000 个样本，所以当我计算 FFT 时。我将有 20000 或 (19999) 个频率箱。我们还假设我的采样率与一些窗口技术相结合可以最大限度地减少频谱泄漏。

那么我的问题是：FFT 是否仍会在 70Hz 时产生相对理想的脉冲？还是会因为原始信号的随机性而“出现”频谱泄漏？换句话说，频率为随机变量的正弦曲线的 FFT 是什么样的？

【问题讨论】：

您需要使用窗函数，基峰周围的裙边形状将取决于您选择的窗函数。

您能否扩展您的问题，w 会随时间变化吗？我的意思是，您的模型是sin(w * t)，其中w 是您的随机变量的恒定实现？或者你的型号是sin(w*t + phi(t))？

【参考方案1】：

一些更常见的调制方案会添加边带，以便在调制中携带信息。根据与 FFT 长度相关的调制量和类型，边带可以与 FFT 峰值分开出现，或者只是“增厚”单个峰值。

【讨论】：

事实上，所有调制方案都会增加带宽，这是傅里叶变换 (en.wikipedia.org/wiki/Fourier_transform#Uncertainty_principle) 的不确定性原理的结果，它表明傅里叶对宽度的乘积基本上是有限。

【参考方案2】：

您的范围会显得更广，这在现实世界中会发生。例如，查看 Voight 曲线，它是 Lorentizan（理想指数衰减的结果）与一定宽度的高斯卷积，宽度由随机波动决定，例如多普勒效应对由窄带激光探测的气体中的分子产生影响。

无论哪种方式，您都不会获得“理想”的频率峰值。 FFT 分辨率的限制是一个频率区间（频率分辨率由时间向量长度的倒数给出），但即使是这样（正如@xvan 指出的那样），窗口函数通常也会扩大。如果您的窗口不存在，即它实际上是时间向量长度的方形窗口，那么您将获得与 sinc 函数卷积的频谱峰值，从而变宽。

对此进行可视化的最佳方法是制作一个长矢量并绘制一个具有足够分辨率的频谱图（通常显示为音频信号），以便您可以看到各个变化。整个信号的 FFT 是移动峰在频谱图垂直轴上的投影。给定时间向量的 FFT 没有任何时间分辨率，而是汇总了 FFT 期间发生的所有频率。因此，频谱图（通常人们简单地使用 STFT，短时傅立叶变换）在任何给定时间都具有“完整”分辨率，即您期望的窄线形。全时向量的 FFT 显示了所有线形的代数和，因此看起来很宽。

总结起来有两个不同的效果： a）从窗口函数扩展（正如评论者 1 和 2 指出的那样） b) 扩大您试图模拟的频率波动的影响，并且这种影响发生在现实生活中（例如，您在接收无线电信号时坐在秋千上）。

最后，请注意@xvan 评论的意义：phi= phi(t)。如果相位角是时间相关的，那么它的导数不为零。 dphi/dt 是一个频移，所以你的瞬时频率变成了f0 + dphi/dt。