python机器学习数学

Posted 2023-04-27

这个代码该如何打

这个题目的意思是平铺一个28*28的numpy二维数组

```python
import numpy as np

def reshape(x):
    return x.flatten()  # 就是这么简单，一行搞定

    
image = np.random.randn(28, 28)
print(reshape(image))
```

顺便问一下，你这个是在哪个网站的习题

参考技术A 不明白怎么打是什么意思，code的内容如下：
import numpy as np
def reshape(x):
x_reshape = 28^2 #计算28*28 参考技术B 虽然机器学习领域没有一个专门的编程语言，但是有很多框架或库都提供基于 Python 的 API（比如 TensorFlow），又或者将 Python 用作建模语言（比如 PyTorch）。如今 Python 虽然在人工智能领域应用广泛，但是也存在一定的弊端 机器学习研究具有极高的计算需求，需要简化建模语言使得添加特定领域的优化和特征变得更加容易。训练模型需要优秀的硬件支持，以及良好的数值、较低的解释器开销和多种并行性的支持。

机器学习数学基础之高数篇——函数极限和导数（python版）

不知道大家有没有类似的经历，斗志满满地翻开厚厚的机器学习书，很快被一个个公式炸蒙了。

想要学习机器学习算法，却很难看的懂里面的数学公式，实际应用只会调用库里的函数，无法优化算法。

学好机器学习，没有数学知识是不行的。数学知识的积累是一个漫长的过程，罗马也不是一夜建成的。

如果想要入门机器学习，数学基础比较薄弱，想打牢相关数学基础，可以关注笔者，一起学习（数学大佬也可以来扫一眼python代码）~

---

接下来我们以高数（同济第七版）课后习题为例，使用python语言来求解函数和导数的习题。

这样大家做课后练习的时候，也可以用python验证一下做的对不对。

这里用到两个常见的Python库，sympy和numpy，学习的时候可以参考官方文档。

sympy 是Python语言编写的符号计算库，这里用于处理数学对象的计算称为符号计算。

官方在线文档：https://docs.sympy.org/dev/index.html

numpy是一个Python库，支持大量的多维数组及矩阵运算，提供用于数组快速操作的各种API。

官方在线文档：https://www.numpy.org.cn/reference/

函数极限

我们来看一下高数课本（同济第七版）对函数极限的定义：

当时上课的时候就觉得这段函数定义太反人类了啊，瞬间打击学习高数的兴趣。

为什么函数极限的定义会这么难以理解呢？

这里需要插入数学史的内容了，这个问题要追溯到几百年前…

古希腊的数学家在处理无穷小和极限问题时，使用穷竭法等方法非常的繁琐。

到了牛顿时代，微积分还不成熟，也就是说牛顿当时也没把无穷小和极限的问题弄明白。

后面一个个大牛都试图把相关的漏洞补齐，我们看到的这个ε-δ定义的极限，是由维尔斯特拉斯总结了前面各个大牛的经验，最终提出来的。

所以最终这个定义我们看不懂也正常，这个概念的形成大约经历了几百年，就算拿给当时的牛顿看也是蒙的呢。

不过这个定义，也是公认的非常严谨、接近本质的函数极限定义了。

光说概念太没意思了，学数学嘛，肯定要做题。我们来看几道高数题吧——

---

函数极限练习题1（高数课后练习1-3第五题 ）：

证明：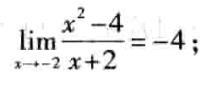

python版证明：

import sympy
from sympy import oo
import numpy as np
x = sympy.Symbol('x')
f = (x ** 2 - 4)/(x + 2)
sympy.limit(f,x,-2)

输出：-4

函数极限练习题2（高数课后习题1-3第6题）：

证明：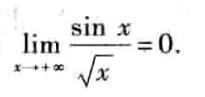

python版证明：

import sympy           #导入sympy符号计算库
from sympy import oo   #oo为无穷大符号
import numpy as np
x = sympy.Symbol('x')
f = sympy.sin(x)/sympy.sqrt(x)
sympy.limit(f,x,oo)    #求极限

输出：0

关于limit的用法，我们来查看官方文档：

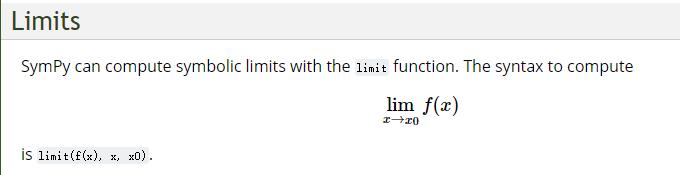
导数

导数定义：

理解了概念，来做几道导数题吧——

导数练习题一（高数 总习题二 第8题（1））：

求下列导数：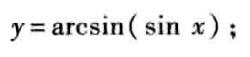

python版求导：

import sympy
from sympy import *
from sympy.abc import x,y
diff(asin(sin(x)))

输出

cos(x)/sqrt(-sin(x)**2 + 1)

python求导数的三种写法

python中求导数主要有三种方法，我们用练习二来演示：

导数练习题二：

求下列导数：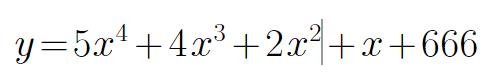

方法一、使用sympy的diff函数。

diff版求导：

import sympy
from sympy import *
from sympy.abc import x,y
diff(5*x**4 + 4*x**3 +2*x**2 + x + 666)

输出：

20*x**3 + 12*x**2 + 4*x + 1

方法二、使用numpy库里的poly1d函数

在官方文档里，查看一下poly1d的用法：

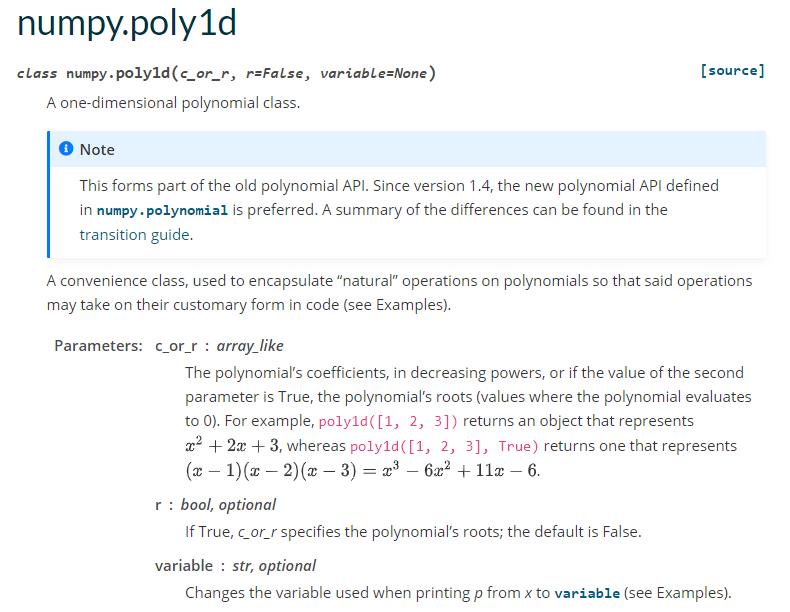
poly1d版求导：

import numpy as np
p = np.poly1d([5,4, 0 ,2 ,1]) #构造多项式，每项是多项式前的系数，幂次由高到低，没有该幂次该项为0
print(np.polyder(p,1)) #求一阶导数
print(p.deriv(1))	   #另一种方法求一阶导数

输出：

    3      2
20 x + 12 x + 2

方法三、使用scipy.misc模块下的derivative函数

在官方文档里，查看一下derivative的用法：

derivative版求导：

import numpy as npfrom scipy.misc 
import derivative
def f(x):    
	return (5*x**4 + 4*x**3 +2*x**2 + x + 666)
print (derivative(f,3,dx=1e-6))  #求x=3时的导数 

输出：

661.0000001501248