matlab 如何判断两线段是不是相交？

Posted 2023-04-27

假设已知四个点A、B、C、D，请用MATLAB语言判断AB与CD是否相交，相交输出1，不相交输出0.大佬帮帮忙！

判断方法比较容易懂，实现要知道这四个点的坐标(Xa,Ya),(Xb,Yb),(Xc,Yc),(Xd,Yd)。

然后得到直线AB的一般表达式f(X,Y)=(Y-Ya)*(Xb-Xa) - (Yb-Ya)*(X-Xa)=0

由于线段CD要跟AB相交，所以将CD两点的坐标代入f(X,Y)所得到的f值相乘小于等于零，所以有f(Xc,Yc)*f(Xd,Yd)<=0，也就是

((Yc-Ya)*(Xb-Xa) - (Yb-Ya)*(Xc-Xa))*((Yd-Ya)*(Xb-Xa) - (Yb-Ya)*(Xd-Xa))<=0

同理得到直线CD的一般表达式g(X,Y)=(Y-Yc)*(Xd-Xc) - (Yd-Yc)*(X-Xc)=0，有

g(Xa,Ya)*g(Xb,Yb)<=0即

 ((Ya-Yc)*(Xa-Xc) - (Yd-Yc)*(Xb-Xc))*((Yb-Yc)*(Xd-Xc) - (Yd-Yc)*(Xb-Xc))<=0

两个都满足那么就相交。

可以这么判断

if(((Yc-Ya)*(Xb-Xa) - (Yb-Ya)*(Xc-Xa))*((Yd-Ya)*(Xb-Xa) - (Yb-Ya)*(Xd-Xa))<=0&&...

        ((Ya-Yc)*(Xa-Xc) - (Yd-Yc)*(Xb-Xc))*((Yb-Yc)*(Xd-Xc) - (Yd-Yc)*(Xb-Xc))<=0)

    fprintf(\'线段相交\\n\');

else

    fprintf(\'线段不相交\\n\');

end

例子：

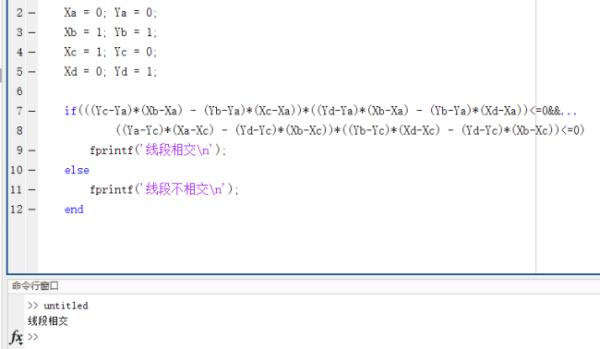
(0,0),(1,1)与(1,0),(0,1)相交的例子

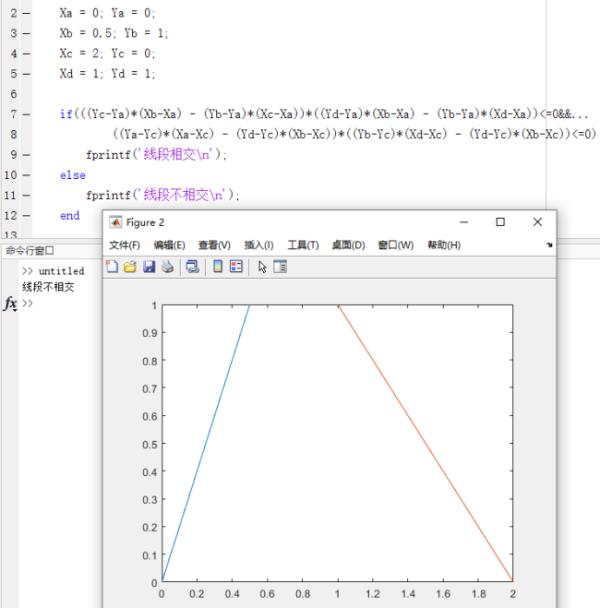
(0,0),(0.5,1)与(2,0),(1,1)不相交例子

追问

您好，您看我这四个点组成的AB和CD两条线段应该是相交的吧，但为什么程序输出结果是不相交？是我哪里出什么问题了吗？希望回答，万分感谢！



追答

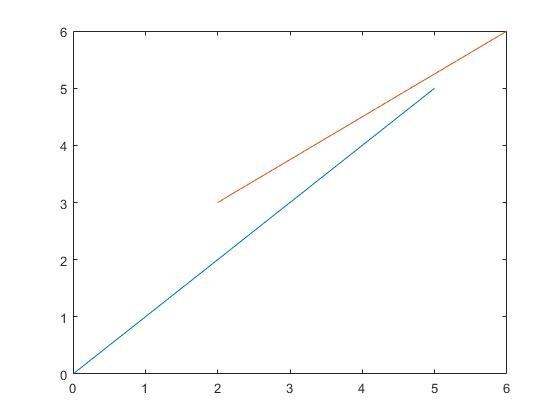
这两条线段哪里相交了？你如果只是判断直线相交，那只要不平行就相交，就不需要那么麻烦了

追问

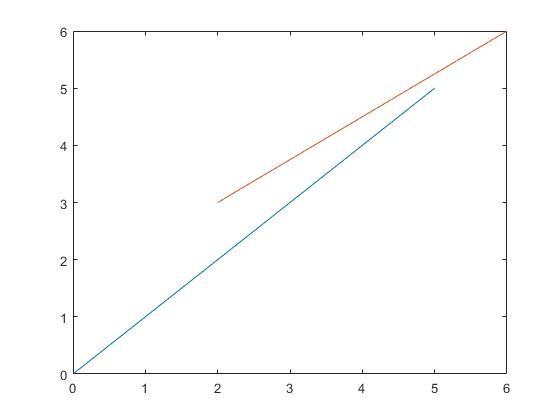
您好，最后一个点是（6,3），不是（6,6）。

追答

不好意思，弄错了一个字符，现在调试正确了：
Xa = 0; Ya = 0;
Xb = 5; Yb = 5;
Xc = 2; Yc = 3;
Xd = 6; Yd = 6;
if(((Yc-Ya)*(Xb-Xa)-(Yb-Ya)*(Xc-Xa))*((Yd-Ya)*(Xb-Xa)-(Yb-Ya)*(Xd-Xa))<=0&&...
((Ya-Yc)*(Xd-Xc)-(Yd-Yc)*(Xa-Xc))*((Yb-Yc)*(Xd-Xc)-(Yd-Yc)*(Xb-Xc))<=0)
fprintf(\'线段相交\\n\');
else
fprintf(\'线段不相交\\n\');
end

参考技术A matlab 如何判断两线段是否相交？
这个问题可以这样思考：
1、用两点式直线方程求出，AB与CD的方程式
2、用solve函数求解该两个方程组成的方程组
3、用if判断语句来判断是否相交，即
有解的，则相交
无解的，则不相交 参考技术B 求两个线段AB和Cd有无公共交点，如果没有就不相交

判断两个线段是否相交

判断两条直线是否相交有两步：

                        1：快速排斥（可以筛除大部分）

                        2：跨立试验（下面会有所说明）

现在开始解释：

    第一步快速排斥，实际上就是先判断一下，假设现在有两条线段ab,cd,现在我们需要判断以ab为对角线的矩形是否和以cd为对角线的矩形是否有重合的部分，如果有则我们可以进行下一步判断，如果没有那么这两条线段肯定不可能相交。

   那么问题来了，我们怎么判断两个矩形是否有重合的部分呢？
   如下图中的两个矩形；

 

 

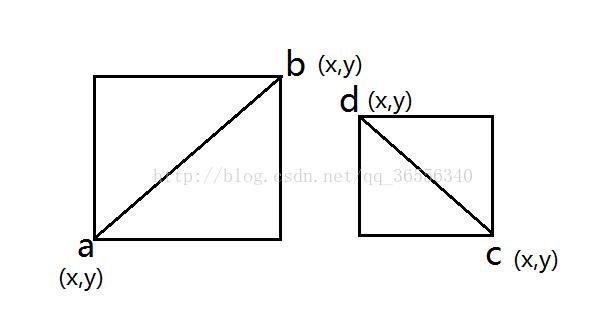
重和的情况：

       对于横向：min(a.x,b.x)<=max(d.x,c.x)&&min(c.x,d.x)<=max(a.x,b.x);

       对于纵向:  min(a.y,b.y)<=max(d.y,c.y)&&min(c.y,d.y)<=max(a.y,b.y);

只有同时满足横向与纵向才能满足两个矩形重合。

     如果满足上面的重合要求后，我们就可以进行第二步判断了，判断是否相互跨立，注意必须是相互跨立。

对于什么是跨立？如果两条线段相交，那么某一条线段的两个端点必定分布在另一条线段的两侧，或者这条直线的端点在另一条直线上。具体情况如下：

 

 

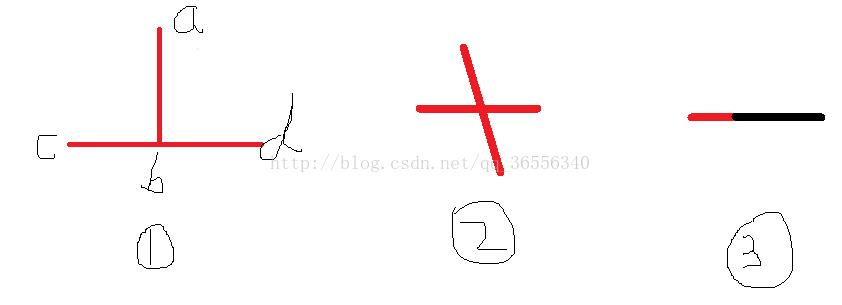
那么这时候我们就可以用叉乘来判断了，没学过的话可以点这个链接 点击打开链接。

如图：

 

 

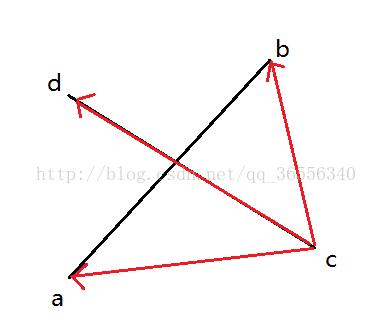
若(ca x cd)*(cb x cd)<=0 则说明ca cb先对于cd的方向不同（叉乘的结果），则a b在线段cd的两侧。

同理若(ac x ab)*(ad x ab)<=0,则可以说明两条线段相互跨立了。

上代码：

 

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
struct node{
double x;
double y;
}; 
node a,b,c,d;
bool judge(node a,node b,node c,node d)
{
if(min(a.x,b.x) <= max(c.x,d.x) && min(c.x,d.x) <= max(a.x,b.x) && min(a.y,b.y) <= max(c.y,d.y) &&min(c.y,d.y)<=max(a.y,b.y))
{

double u,v,w,z;//保存叉乘 
u=(c.x-a.x)*(b.y-a.y)-(b.x-a.x)*(c.y-a.y);
v=(d.x-a.x)*(b.y-a.y)-(b.x-a.x)*(d.y-a.y);
w=(a.x-c.x)*(d.y-c.y)-(d.x-c.x)*(a.y-c.y);
z=(b.x-c.x)*(d.y-c.y)-(d.x-c.x)*(b.y-c.y);
return (u*v<=0.00000001 && w*z<=0.00000001); //浮点数判断大小
}
return false;
}
int main()
{
cin >> a.x >> a.y;
cin >> b.x >> b.y;
cin >> c.x >> c.y;
cin >> d.x >> d.y;
if(judge(a,b,c,d))
{
printf("相交\\n");
}
else
{
printf("不相交\\n");
}
return 0;
}

 

水波，借鉴某位大佬的图，thanks。
---------------------
作者：白黑菜
来源：CSDN
原文：https://blog.csdn.net/qq_36556340/article/details/70039800
版权声明：本文为博主原创文章，转载请附上博文链接！