梯度下降法改进过程：从 SGD 到 Adam算法

Posted 2023-04-20

参考技术A

梯度g 指函数的某处的偏导数，指向函数上升方向。因此梯度下降法是指用梯度的负数-g更新参数，从而使下一次计算的结果向函数下降方向逼近，从而得到最小值。其中更新时乘的系数称为 学习率 。

以所有m个数据作为一个批次，每次计算损失loss值和梯度g（偏导）时为所有数据的累加和，更新每个参数时也都是以所有数据的梯度累加和进行计算更新。
优点： 下降方向为全局最优值 缺点： 计算所有数据的梯度非常耗时

虽然m个数据为一个批次，但是更新参数时仅使用随机一个数据的梯度进行更新。
优点： 很快 缺点： 随机性高，噪声影响严重，不一定向整体最优点下降。

把所有样本分为n个batch（一般是随机的），每次计算损失和梯度时用一个batch的数据进行计算，并更新参数，从而避免了唯一随机性和全局计算的耗时性。
优点： 得到的梯度下降方向是局部最优的，整体速度快。

参考： 知乎专栏-SGD

梯度下降法可能会停滞到 平原、鞍点和局部最优点（在这三个点梯度均为0） ，因此带动量的梯度下降法能依靠之前的梯度值，“冲过平原、鞍点和局部最优点”，提高泛化性。

参考： 知乎专栏-动量 ， 简述动量csdn

Adagard 针对不同的变量提供不同的学习率。 当一些变量被优化到最优点，但另外一些变量没到最优点，使用统一的学习率就会影响优化过程，太大或太小都不合适。太大不容易收敛，太小收敛缓慢。
解决方式： 为每一参数建立历史累计梯度值，利用历史累计梯度作为分母，从而使各个参数在训练后期被给予不同的除数，得到自适应参数值 。

参考： 知乎专栏

Adagard 暴力累加参数之前的所有梯度平方作为分母进行自适应（二阶梯度的梯度下降？），而RMSprop进行历史梯度平方和的加权；
用 来控制衰减程度（通常为0.9），每次不再直接累加，而是一个指数移动平均，即是 用二阶梯度的移动平均代替当前梯度进行更新参数 。

参考： 知乎专栏-RMSprop

Adam 可以看做 RMSprop 与 Momentum 的结合，使用了一阶梯度的指数移动平均（Momentum)和二阶梯度的指数移动平均（RMSprop）。
优点 :每一次迭代学习率都有一个明确的范围,使得参数变化很平稳.
注意到，在迭代初始阶段， 和 有一个向初值的偏移（过多的偏向了 0）。因此，可以对一阶和二阶动量做偏置校正 (bias correction)，

机器学习：SGD随机梯度下降法

1.梯度下降

   1）什么是梯度下降？

         因为梯度下降是一种思想，没有严格的定义，所以用一个比喻来解释什么是梯度下降。

        

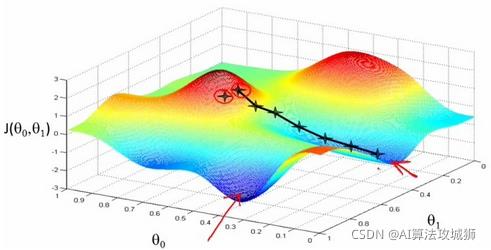
        简单来说，梯度下降就是从山顶找一条最短的路走到山脚最低的地方。但是因为选择方向的原因，我们找到的的最低点可能不是真正的最低点。如图所示，黑线标注的路线所指的方向并不是真正的地方。

        既然是选择一个方向下山，那么这个方向怎么选？每次该怎么走？

       先说选方向，在算法中是以随机方式给出的，这也是造成有时候走不到真正最低点的原因。

       如果选定了方向，以后每走一步，都是选择最陡的方向，直到最低点。

       总结起来就一句话：随机选择一个方向，然后每次迈步都选择最陡的方向，直到这个方向上能达到的最低点。

      2）梯度下降是用来做什么的?

       在机器学习算法中,有时候需要对原始的模型构建损失函数,然后通过优化算法对损失函数进行优化，以便寻找到最优的参数，使得损失函数的值最小。而在求解机器学习参数的优化算法中，使用较多的就是基于梯度下降的优化算法(Gradient Des