在SPSS中如何删除箱形图显示的极端值？

Posted

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了在SPSS中如何删除箱形图显示的极端值？相关的知识，希望对你有一定的参考价值。

1、删除与之对应的数据集内的数据行。
2、变量较多，箱形图有几十个。

做出来箱图的结果后，如图1，发现极端值。双击图形进入编辑器，选择上方套索更具，如图2。之后用套索工具将极端值圈出，选择上方“转至个案”按钮，如图3。之后就能看到极端值个案，Delete删除即可。

 参考技术A

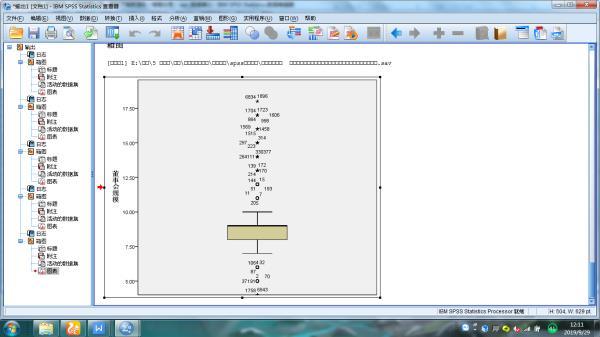
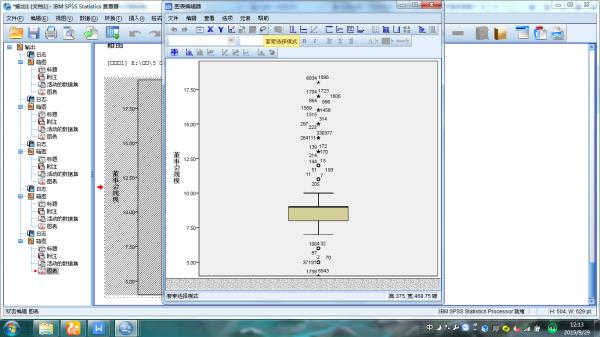
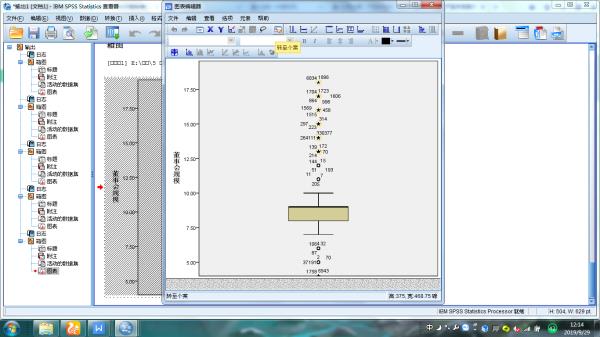
可以直接把极端值变成白色（与背景色一致），这样即使存在极端值，在图中看不出来。

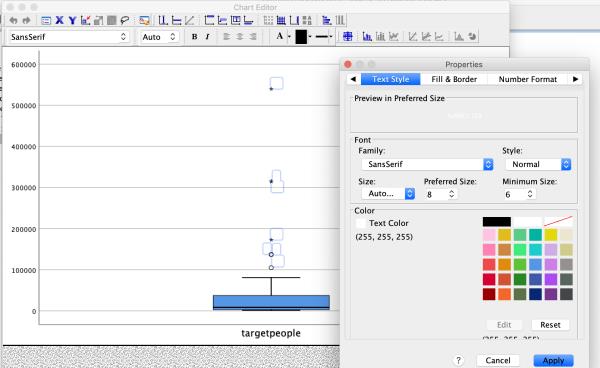
具体方法是：双击图形，点击极端值（选中所有极端值代码），字体白色。

如图所示：

 参考技术B 图里可以右键选项,选择显示离群值的编号的 我经常帮别人做类似的数据分析的，如果能帮助到你，把我回答的问题设置为“好评”。本回答被提问者采纳

可视化神器Plotly玩转箱形图

可视化神器Plotly玩转箱形图

在之前的文章中介绍过如何使用Plotly绘制柱状图、饼图、散点图等，都是比较常用的可视化图表呈现方式。本文介绍的是利用Plotly绘制统计图形中的一种：箱型图。

扩展阅读

Plotly的文章会形成连载系列，前面8篇Plotly可视化文章分别是：

箱型图

什么是箱型图

箱型图是一种用作显示一组数据分散情况资料的统计图，它能够快速显示数据中的异常值情况，其形状像盒子，因而得名，也称之为盒须图、盒式图、盒装图或者箱型图。

1977年，美国著名数学家John W. Tukey首先在他的著作《Exploratory Data Analysis》中介绍了箱形图。

四分位数

四分位数是箱型图中最为重要的概念，下面介绍四分位数的相关知识。

四分位数（Quartile）是统计学中分位数的一种，即把所有数值由小到大分成四等份，处于三个分割点位置的数值就是四分位数。

  • 第一四分位数（Q1）：也称下四分位数（Lower Quartile），等于该样本中所有数值由小到大排列后第25%的数字。
  • 第二四分位数（Q2）：也称中位数（Middle Quartile or Median），等于该样本中所有数值由小到大排列后第50%的数字。
  • 第三四分位数（Q3）：也称上四分位数（Upper Quartile），等于该样本中所有数值由小到大排列后第75%的数字。

Q3和Q1的差距称为四分位距（InterQuartile Range， IQR）：IQR=Q3-Q1

四分位数计算

在计算四分位数的时候我们需要先计算四分位数的位置，3个四分位数的位置计算：

# n表示样本个数
Q1的位置 = (n+1) / 4
Q2的位置 = (n+1) * 2 / 4
Q3的位置 = (n+1) * 3 / 4

通过一个例子来进行讲解位置的计算，有11个数值无序排列如下：

6, 47, 49, 15, 42, 41, 7, 39, 43, 40, 36

我们先将数值按照从小到大排列：

6, 7, 15, 36, 39, 40, 41, 42, 43, 47, 49

那么3个四分位数的位置分别为：

# n=11表示样本个数
Q1的位置 = (11+1) / 4 = 3
Q2的位置 = (n+1) * 2 / 4 = 6
Q3的位置 = (n+1) * 3 / 4 = 9

对应的3个四分位数为：Q1=15，Q2=40，Q3=43，IQR=Q3-Q1=28

如果计算出来位置刚好不是整数，即n+1不是4的整数倍，则一般取该位置两边数的加权平均值（也有直接取平均值的），位置离得越近的数值权重越高，一般权重为：1−小数位。比如对于以下样本：

2,3,4,5

那么计算Q1的位置为：（4+1）/ 4= 1.25，且更靠近2，那么Q1为：

Q1=2 * (1 - 0.25) + 3 * 0.25 = 2.25   # 0.25是小数位

如果直接取平均值：Q1= (2+3) / 2 = 2.5

4种不同箱型图比较

来自维基百科上4种不同箱型图的比较：

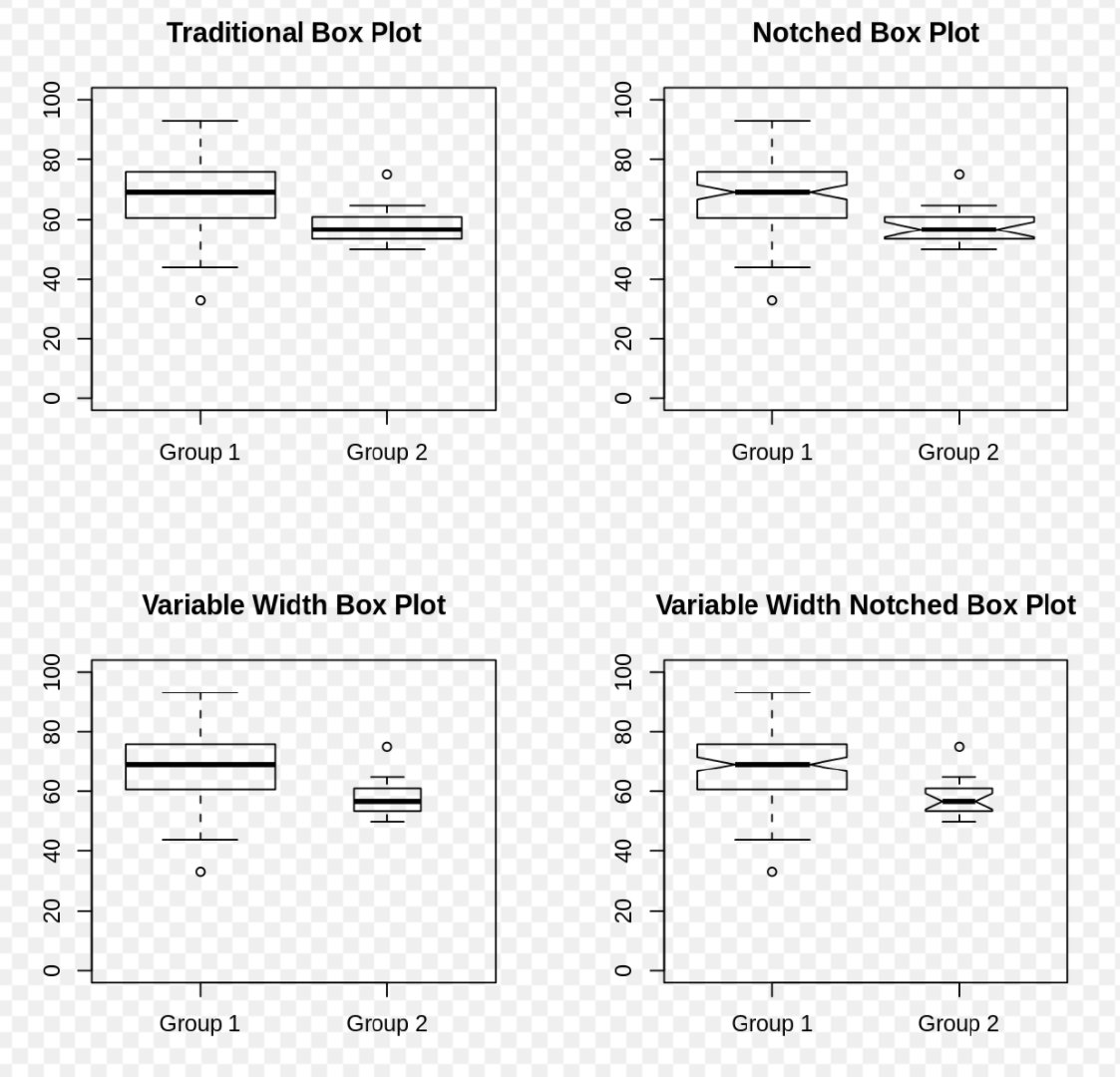
箱型图作用

  • 它可以粗略地看出数据是否具有有对称性
  • 显示数据分布的分散程度等信息，特别可以用于对几个样本的比较。
  • 反映一组或多组连续型定量数据分布的中心位置和散布范围
  • 分析不同类别数据各层次水平差异，还能揭示数据间离散程度、异常值、分布差异等

箱形图最大的优点就是不受异常值的影响，能够准确稳定地描绘出数据的离散分布情况，同时也利于数据的清洗。

数据集

下面介绍各种需求场景下箱型图的绘制，本文中使用的数据大部分是plotly中自带的消费tips数据集：

import pandas as pd
import numpy as np

import plotly_express as px
import plotly.graph_objects as go

# 消费数据集
tips = px.data.tips()
tips.head()

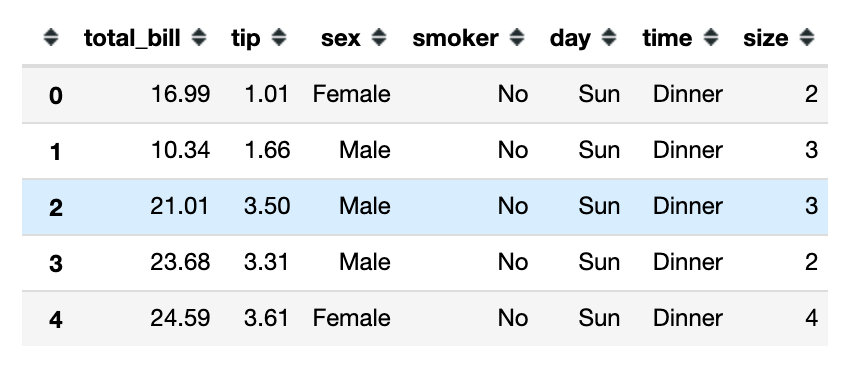
本文绘图使用的也是两种方法：

import plotly_express as px  # 1、px实现
import plotly.graph_objects as go  # 2、go实现

基于px绘制箱型图

基于点的箱体图

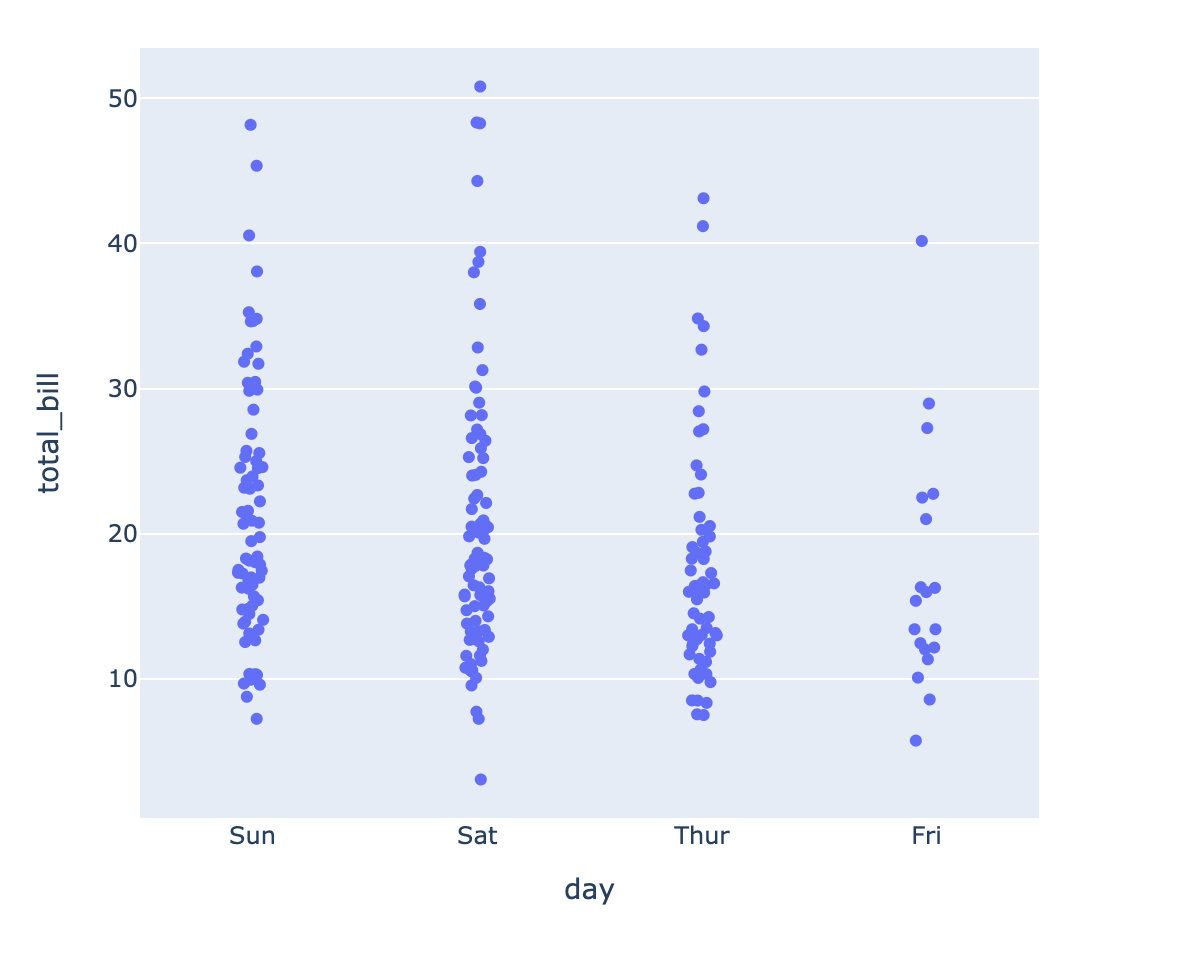
使用每个数据的点作为标记marker来绘制箱体图，使用的方法是：px.strip()

# 使用的方法是：px.strip()

fig = px.strip(
    tips,
    x='day',  # 星期
    y='total_bill'  # 总账单
)

fig.show()


# 使用的方法是：px.strip()

fig = px.strip(
    tips,
    x='time',  # 中餐还是晚餐  
    y='tip'  # 小费
)

fig.show()

基础箱型图

fig = px.box(
  tips,  # 数据集
  y="total_bill"  # 针对哪个字段的数据做箱型图
)

fig.show()

分组箱体图

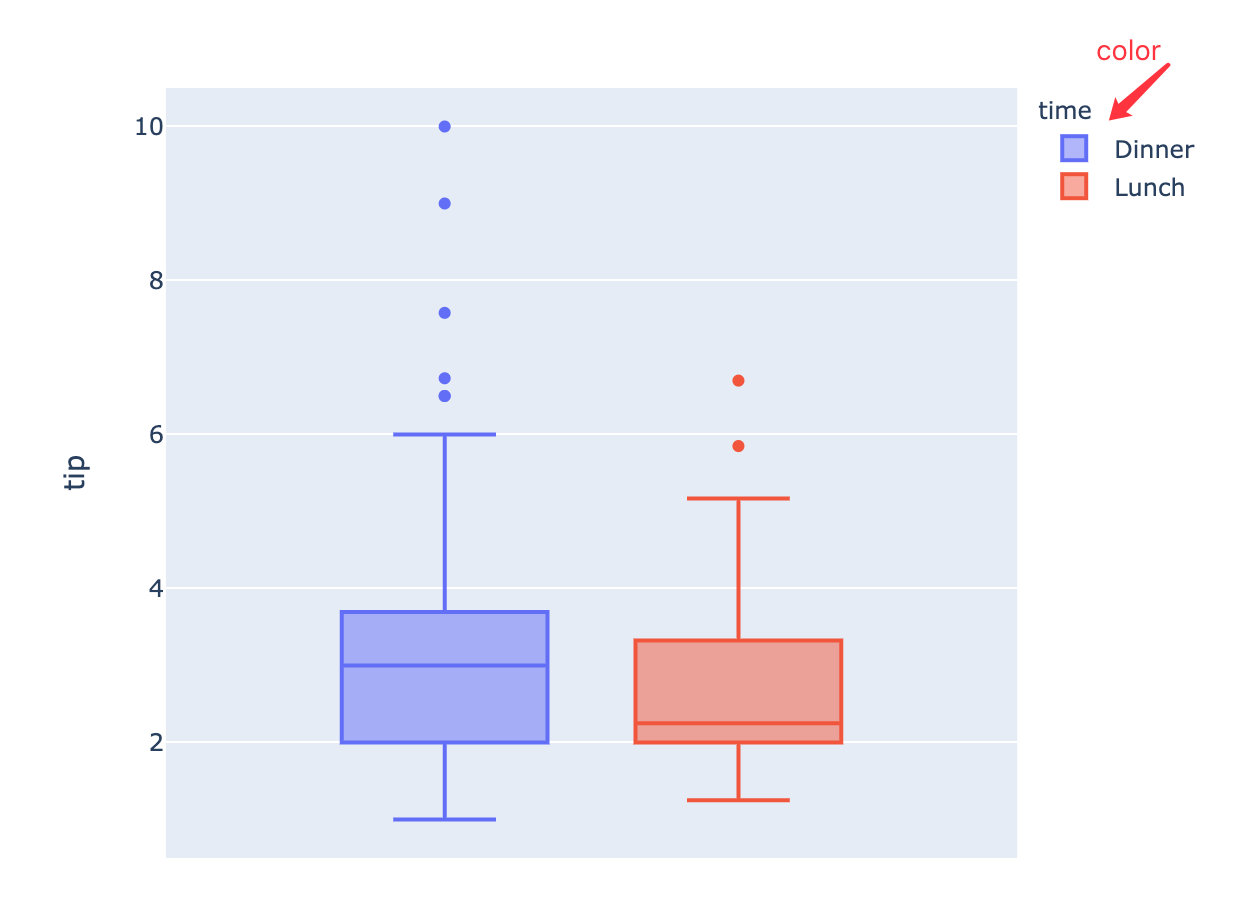
针对有不同分类的组绘制箱体图：

fig = px.box(
  tips,  # 数据集
  y="tip",  # 绘图字段
  color="time"  # 颜色字段
)

fig.show()

再来一个稍微多字段的分组箱体图：

fig = px.box(
    tips,
    x="day",   # 分组的数据
    y="total_bill",  # 箱体图的数值
    color="day"  # 颜色分组
)

fig.show()

带散点的箱体图

有时候我们在绘制箱体图的时候，需要带上散点，散点表示的就是原始数据情况。点的取值有4种情况：

  • all：全部
  • outliers：离群点
  • suspectedoutliers：可疑离群点
  • False：不显示
fig = px.box(
    tips,
    x="day",
    y="total_bill",
    points="all"   # ['all', 'outliers', 'suspectedoutliers', False]
)

fig.show()

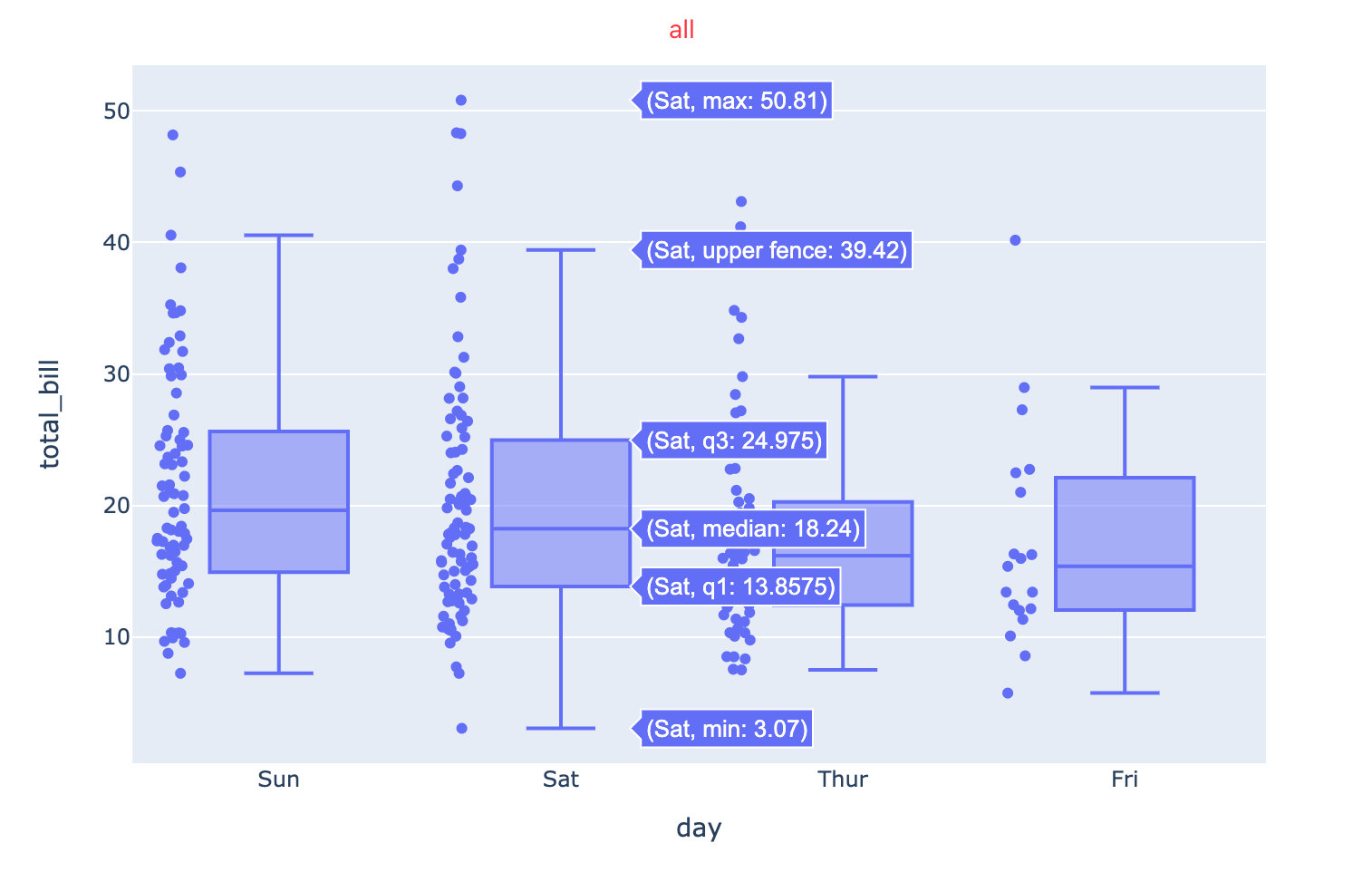
带四分位数的箱体图

计算散点插值方法有3种：

  • linear：线性差值方法，默认
  • exclusive：排除算法统计。如果样本是奇数，则不包含任何一半的中位数，Q1是下半部分的中位数，Q3是上半部分的中位数
  • inclusive：包含算法统计；如果样本是奇数，则在两个半部分都包含中位数，Q1是下半部分的中位数，Q3是上半部分的中位数
fig = px.box(
    tips, 
    x="day",
    y="tip",
    color="smoker")

fig.update_traces(quartilemethod="exclusive") # exclusive inclusive linear (默认)

fig.show()

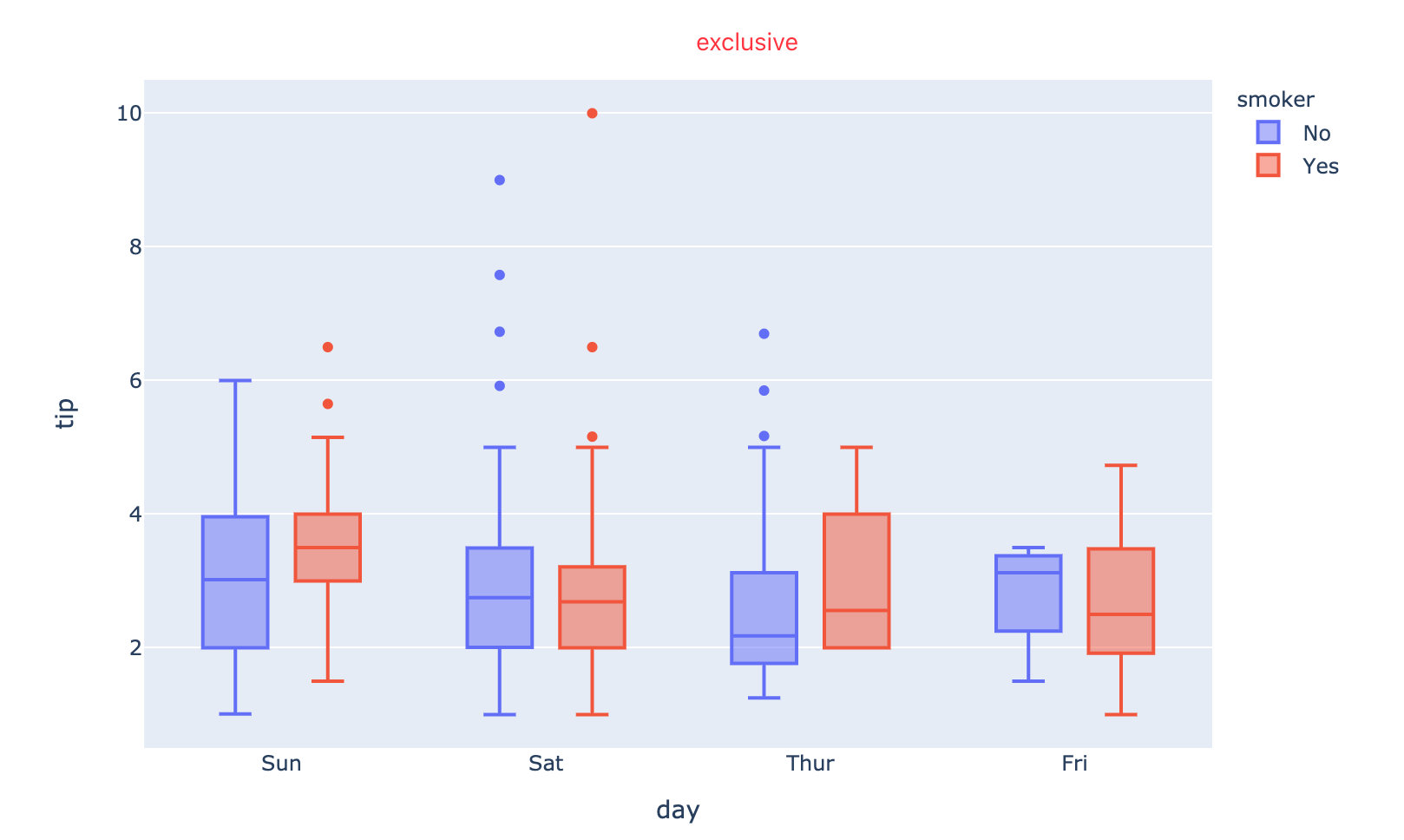
3种不同四分位数显示方法比较

模拟一份数据集：

data = [10,20,30,40,50,60,70,80,90]

pd.DataFrame(dict(
    linear=data,
    inclusive=data,
    exclusive=data
))

# 下面是数据的部分截图

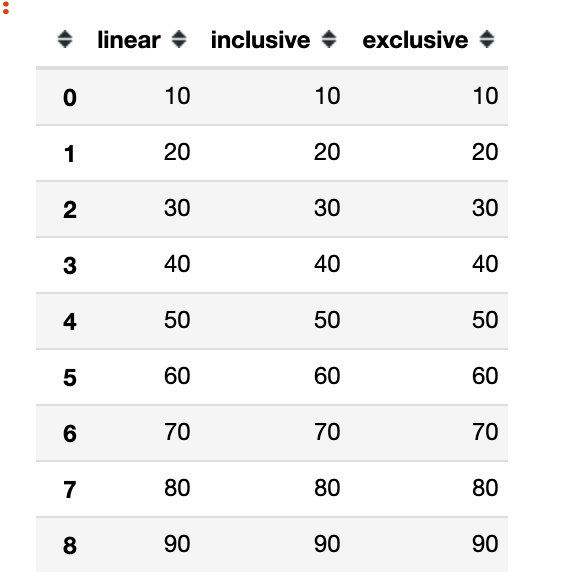
使用melt方法对上面的数据进行合并和转化，使用到了一个melt函数：

  • d_vars:不需要被转换的列名
  • value_vars:需要转换的列名，如果剩下的列全部都要转换，就不用写
  • var_name和value_name是自定义设置对应的列名。
  • col_level：如果列是MultiIndex，则使用此级别
## 3种不同算法之间的比较结果

import plotly.express as px
import pandas as pd

data = [10,20,30,40,50,60,70,80,90]

df = pd.DataFrame(dict(
    linear=data,
    inclusive=data,
    exclusive=data
)).melt(var_name="quartilemethod")  # 宽表转成长表

df

添加数据轨迹和抖动间距jitter：

fig = px.box(
    df, 
    y="value", 
    facet_col="quartilemethod", 
    color="quartilemethod",
    boxmode="overlay", 
    points='all')

# jitter：数据抖动 =0表示没有抖动，点和点的距离是均衡的
fig.update_traces(quartilemethod="linear", jitter=0, col=1)
fig.update_traces(quartilemethod="inclusive", jitter=0, col=2)
fig.update_traces(quartilemethod="exclusive", jitter=0, col=3)

fig.show()

带缺口的箱体图

fig = px.box(
    tips,
    x="day",
    y="tip",
    color="smoker",
    notched=True,  # 显示缺口
    title="小费数据集箱体图",
    hover_data = ["day"]
)

fig.show()

基于go绘制箱型图

基础箱体图绘制

import plotly.graph_objects as go

fig = go.Figure(data=[go.Box(
    y=[0, 1, 1, 2, 4, 7, 9, 15, 21],
    boxpoints='all', # all、outliers 、suspectedoutliers、False
    jitter=0.3, # 数据点之间添加抖动
    pointpos=-1.5   # 点和箱体之间的距离，参数范围：[-2, 2]
      )])

fig.show()

分组箱体图绘制

np.random.seed(1)  # 设置随机种子

y1 = np.random.randn(60) - 1   # 随机生成60个数据
y2 = np.random.randn(60) - 1


fig = go.Figure()

# 添加两个数据轨迹，形成图形
fig.add_trace(go.Box(y=y1)) 
fig.add_trace(go.Box(y=y2))

fig.show()

我们还可以设置图形的颜色：

fig = go.Figure()

# 添加两个数据轨迹，形成图形
fig.add_trace(go.Box(y=y1,  # 数值
                     name="图1",  # 轨迹名称
                     marker_color="red" # 颜色
                    )) 

fig.add_trace(go.Box(y=y2,
                     name="图2",
                     marker_color="lightseagreen"
                    ))

fig.show()


import plotly.graph_objects as go

x = ['day 1', 'day 1', 'day 1', 'day 1', 'day 1', 'day 1',
     'day 2', 'day 2', 'day 2', 'day 2', 'day 2', 'day 2']

fig = go.Figure()

fig.add_trace(go.Box(
    x=x,
    y=[0.2, 0.2, 0.6, 1.0, 0.5, 0.4, 0.2, 0.7, 0.9, 0.1, 0.5, 0.3],
    name='kale',
    marker_color='#3D0970'
))

fig.add_trace(go.Box(
    x=x,
    y=[0.6, 0.7, 0.3, 0.6, 0.0, 0.5, 0.7, 0.9, 0.5, 0.8, 0.7, 0.2],
    name='radishes',
    marker_color='#0F4136'
))

fig.add_trace(go.Box(
    x=x,
    y=[0.1, 0.3, 0.1, 0.9, 0.6, 0.6, 0.9, 1.0, 0.3, 0.6, 0.8, 0.5],
    name='carrots',
    marker_color='#FA851B'
))

fig.update_layout(
    yaxis_title='数值',
    boxmode='group' # 柱状图模式
)
fig.show()

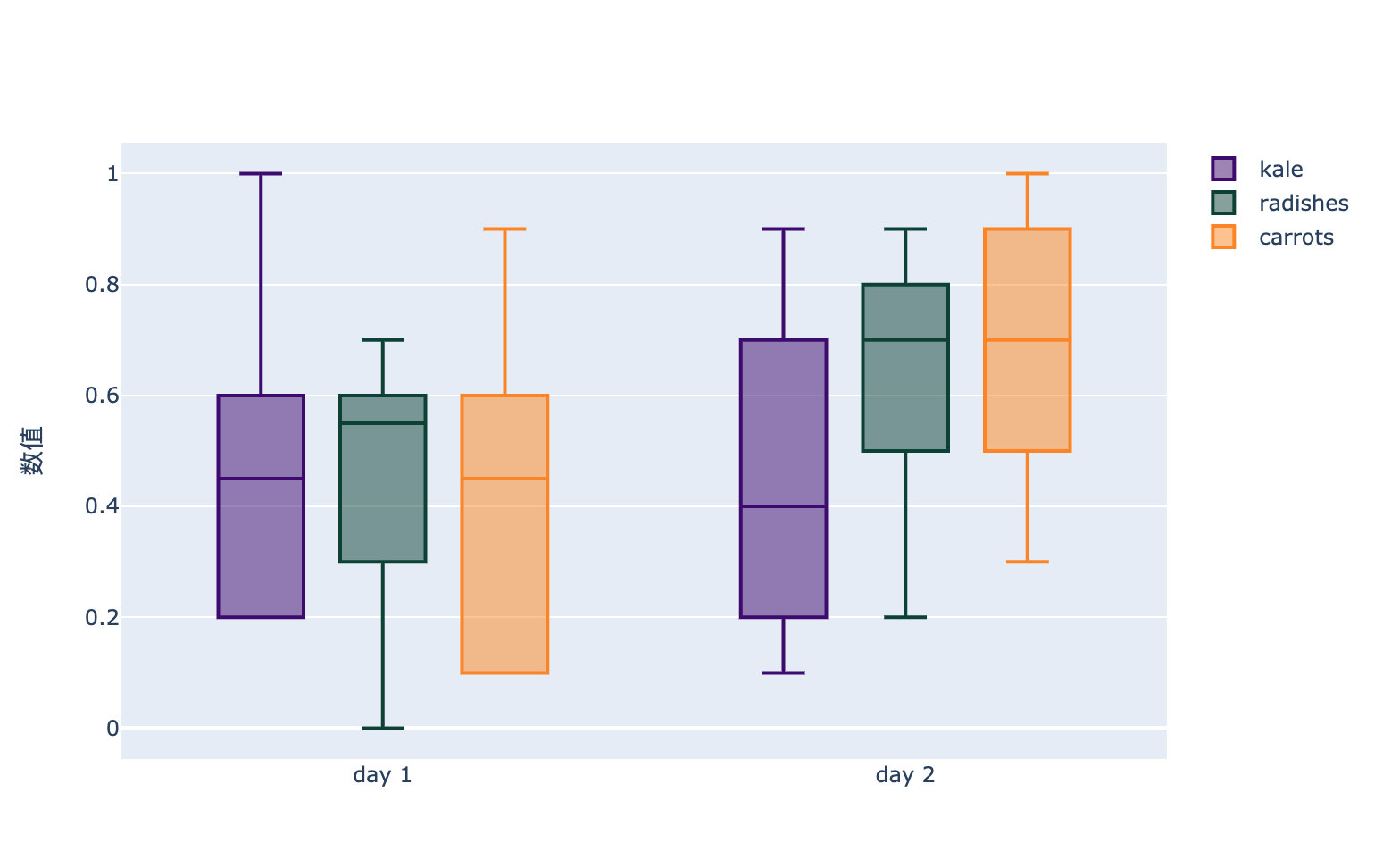
全样式箱体图

import plotly.graph_objects as go

# x轴数据
x_data = ['小明', '小红','小周', '小孙','小张', '小苏']

N = 80

# 生成y轴数据：生成数据同时指定数据类型
y0 = (10 * np.random.randn(N) + 60).astype(np.int)
y1 = (13 * np.random.randn(N) + 78).astype(np.int)
y2 = (11 * np.random.randn(N) + 83).astype(np.int)
y3 = (9 * np.random.randn(N) + 76).astype(np.int)
y4 = (15 * np.random.randn(N) + 91).astype(np.int)
y5 = (12 * np.random.randn(N) + 80).astype(np.int)

y_data = [y0, y1, y2, y3, y4, y5]

# 颜色设置
colors = ['rgba(93, 164, 214, 0.5)', 
          'rgba(155, 144, 14, 0.5)', 
          'rgba(44, 160, 101, 0.5)',
          'rgba(155, 65, 54, 0.5)', 
          'rgba(27, 114, 255, 0.5)',
          'rgba(127, 96, 0, 0.5)']

fig = go.Figure()

# 通过zip函数生成6组不同的函数进行轨迹添加
# 生成不同的轨迹
for xd, yd, cls in zip(x_data, y_data, colors):
        fig.add_trace(go.Box(
            y=yd,  # y轴数据
            name=xd,  # 名称
            boxpoints='all',  # 箱体散点的显示
            jitter=0.5,  # 抖动距离
#             whiskerwidth=0.2,
            fillcolor=cls,  # 颜色
            marker_size=2,  # 标记大小
            line_width=1)  # 线宽
        )

# 布局设置
fig.update_layout(
    title='6名同学成绩比较',
    yaxis=dict(
        autorange=True,
        showgrid=True,  # 显示网格
        zeroline=True,  # 0基准线
        dtick=5,
        gridcolor='rgb(255, 255, 255)',  # 网格和基准线设置
        gridwidth=1,
        zerolinecolor='rgb(255, 255, 255)',
        zerolinewidth=2,
    ),
    margin=dict(
        l=40,
        r=30,
        b=80,
        t=100,
    ),
    paper_bgcolor='rgb(243, 243, 243)',  # 背景设置
    plot_bgcolor='rgb(243, 243, 243)',
    showlegend=True  # 显示图例
)

fig.show()

3种不同方式下四分位数的显示

对3种不同计算方法下四分位数的显示：

import plotly.graph_objects as go

data = [1, 2, 3, 4, 5, 6, 7, 8, 9]
fig = go.Figure()

fig.add_trace(go.Box(y=data, quartilemethod="linear", name="Linear Quartile"))
fig.add_trace(go.Box(y=data, quartilemethod="inclusive", name="Inclusive Quartile"))
fig.add_trace(go.Box(y=data, quartilemethod="exclusive", name="Exclusive Quartile"))

fig.update_traces(
    boxpoints='all',   # ['all', 'outliers', 'suspectedoutliers', False]
    jitter=0  # 没有抖动，点和点的距离是相同的
)

fig.show()

通过上图可以清楚地看到3种不同差值方法的区别。

水平箱型图

x1 = np.random.randn(50)
x2 = np.random.randn(50) + 5

fig = go.Figure()
fig.add_trace(go.Box(x=x1))
fig.add_trace(go.Box(x=x2))

fig.show()

分组水平箱型图

import plotly.graph_objects as go

y = ['day 1', 'day 1', 'day 1', 'day 1', 'day 1', 'day 1',
     'day 2', 'day 2', 'day 2', 'day 2', 'day 2', 'day 2']

fig = go.Figure()

fig.add_trace(go.Box(
    y=y,
    x=[0.2, 0.2, 0.6, 1.0, 0.5, 0.4, 0.2, 0.7, 0.9, 0.1, 0.5, 0.3],
    name='kale',
    marker_color='#3D0970'
))

fig.add_trace(go.Box(
    y=y,
    x=[0.6, 0.7, 0.3, 0.6, 0.0, 0.5, 0.7, 0.9, 0.5, 0.8, 0.7, 0.2],
    name='radishes',
    marker_color='#0F4136'
))

fig.add_trace(go.Box(
    y=y,
    x=[0.1, 0.3, 0.1, 0.9, 0.6, 0.6, 0.9, 1.0, 0.3, 0.6, 0.8, 0.5],
    name='carrots',
    marker_color='#FA851B'
))

fig.update_layout(
#     xaxis_title='数值',
    xaxis=dict(
        title="数值",
        zeroline=False
    ),
    boxmode='group' # 柱状图模式
)

fig.update_traces(orientation='h')  # 水平柱状图
fig.show()

带有均值和方差的箱体图

import plotly.graph_objects as go

fig = go.Figure()
fig.add_trace(go.Box(
    y=np.random.randn(50),
    name='均值',
    marker_color='mediumblue',
    boxmean=True # 仅仅存在均值
))
fig.add_trace(go.Box(
    y=np.random.randn(50),
    name='均值和标准差',
    marker_color='red',
    boxmean='sd' # 表示同时存在均值和标准差
))

fig.show()

4种不同数据点的显示方式

import plotly.graph_objects as go

y_data = [0.75, 5.25, 5.5, 6, 6.2, 6.6, 
       6.80, 7.0, 7.2, 7.5, 7.5, 7.75, 
       8.15,8.15, 8.65, 8.93, 9.2, 9.5, 
       10, 10.25, 11.5, 12, 16, 20.90, 
       22.3, 23.25]

fig = go.Figure()

fig.add_trace(go.Box(
    
    y=y_data,
    
    name="全部数据点",
    jitter=0.3,  # 抖动距离
    pointpos=-1.8,  # 散点和箱体图的距离
    boxpoints='all', #  all：显示全部数据点
    marker_color='rgb(7,40,89)',
    line_color='rgb(7,40,89)'
))

fig.add_trace(go.Box(
    y=y_data,
    name="晶须线",
    boxpoints=False, # 没有数据点，只有晶须线
    marker_color='rgb(109,56,125)',
    line_color='rgb(9,56,125)'
))

fig.add_trace(go.Box(
    y=y_data,
    name="可疑离群点",
    boxpoints='suspectedoutliers', # 可疑离群点
    marker=dict(
        color='rgb(8,81,156)',
        outliercolor='rgba(219, 64, 82, 0.6)',
        line=dict(
            outliercolor='rgba(219, 64, 82, 0.6)',
            outlierwidth=2)),
    line_color='rgb(8,81,156)'
))

fig.add_trace(go.Box(
    y=y_data,
    name="晶须+离群点",
    boxpoints='outliers', # 仅显示离群点
    marker_color='rgb(107,174,14)',
    line_color='rgb(107,174,214)'
))

fig.update_layout(title_text="基于个性化离群值的散点图")
fig.show()

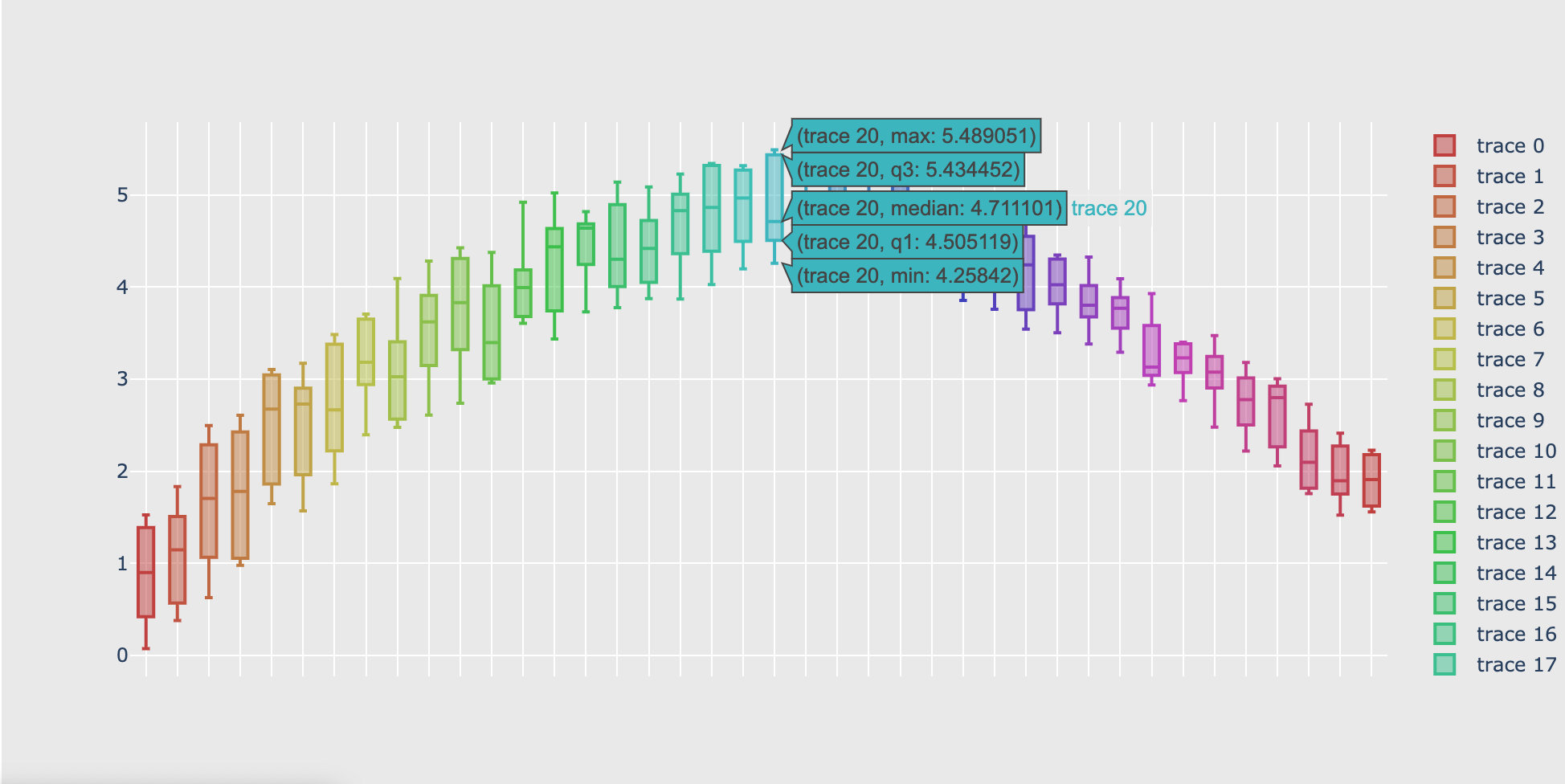
彩虹箱型图

import plotly.graph_objects as go
import numpy as np

N = 40     # 箱体图的个数
c = ['hsl('+str(h)+',50%'+',50%)' for h in np.linspace(0, 360, N)]

具体的绘图代码为：

fig = go.Figure(data=[go.Box(
    # 使用三角函数来绘制图形
    y=3.5 * np.sin(np.pi * i/N) + i/N + (1.5 + 0.5 * np.cos(np.pi*i/N)) * np.random.rand(10),
    marker_color=c[i]
    ) for i in range(int(N))])

# 布局设置
fig.update_layout(
    # xy轴设置
    xaxis=dict(showgrid=True, 
               zeroline=False, 
               showticklabels=False),
    yaxis=dict(zeroline=False, 
               gridcolor='white'),
    # 背景颜色设置
    paper_bgcolor='rgb(233,233,233)',
    plot_bgcolor='rgb(233,233,233)',
)

fig.show()

以上是关于在SPSS中如何删除箱形图显示的极端值？的主要内容，如果未能解决你的问题，请参考以下文章

如何在箱形图dc.js中仅显示有限数量的记录

在 ggplot2-R 中编辑和格式化箱形图（删除时间序列图中的列和箱宽）

R数据可视化2:箱形图 Boxplot

如何删除spss中不需要的数据

你如何改变熊猫箱形图Y轴的传播？

箱线图（Box Plot）理论篇