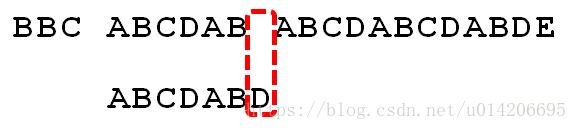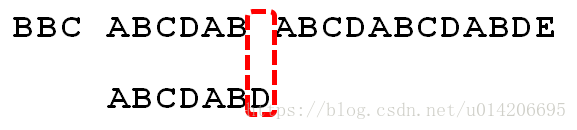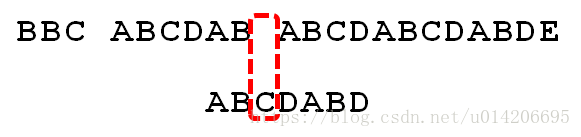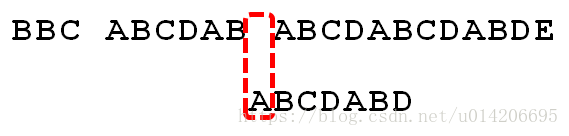算法基础 - 朴素模式匹配算法、KMP模式匹配算法

Posted 2023-04-15

参考技术A 假设我们要从 主字符串goodgoogle 中匹配 子字符串google
朴素模式匹配算法就是 通过从主字符的头部开始 一次循环匹配的字符串的挨个字符 如果不通过 则主字符串头部位置遍历位置+1 在依次遍历子字符串的字符

匹配过程
主字符串从第一位开始 取出g 子字符串取出第一位 g 匹配 进入子循环
取出o 取出o 匹配
取出o 取出o 匹配
取出d 取出g 不匹配 主字符串遍历位置+1

主字符串从第二位开始 取出o 子字符串取出第一位 g 不匹配 主字符串遍历位置+1

主字符串从第三位开始 取出o 子字符串取出第一位 g 不匹配 主字符串遍历位置+1

主字符串从第四位开始 取出d 子字符串取出第一位 g 不匹配 主字符串遍历位置+1

主字符串从第五位开始 取出g 子字符串取出第一位 g 匹配 进入子循环
取出o 取出o 匹配
取出o 取出o 匹配
取出g 取出g 匹配
取出l 取出l 匹配
取出e 取出e 匹配 子循环结束 匹配成功

假设主字符串 长度为 n 子字符串长度为m n>= m
最好的情况需要匹配m次 时间复杂度为 0(m)

例如 000000000001 匹配 00001 每次进入子循环之后 都要遍历到最后一次子循环才得出不匹配
需要匹配次数 (n-m+1) * m
最坏的情况需要匹配m次 时间复杂度为 0((n-m+1) * m)

KMP 算法的主要核心就是 子字符串在子循环内得出不匹配时 主字符串当前的判断位不需要回溯–也就是不可以变小 ，且子循环的判断位需要回溯 回溯位与子字符串本身是否具有重复结构有关 。 以此来规避无效的判断
时间复杂度为 O(n+m)

如果主串 S = "abcdefgab" 我们要匹配的子串 T = "abcdex" 如果用前面的朴素算法 ， 前5个字母完全相同
直到第6个字母 f 和 x 不同
步骤1
S: a b c d e f g a b
T: a b c d e x

接下来如果用朴素算法的话 那么应该是如下比较
步骤2
S: a b c d e f g a b
T: # a b c d e x
b 和 a 不匹配

步骤3
S: a b c d e f g a b
T: # # a b c d e x
a和c 不匹配

步骤4
S: a b c d e f g a b
T: # # # # a b c d e x
d和a 不匹配

步骤5
S: a b c d e f g a b
T: # # # # a b c d e x
a和e 不匹配

步骤6
S: a b c d e f g a b
T: # # # # # a b c d e x

即主串S中的第2 ，3 ， 4， 5， 6 位都与子串T的首字符不相等

对于子串T来说 如果首字符a与后面的bcdex中任意一个字符都不相等
那么对于上面的第一步来说 前五位都相等 那么 可以得到 子串首字符a 与主串的第2，3，4，5 位都不相等
即步骤2 ， 3 ，4 ，5 都是多余的 可以直接进入步骤6

如果子串的首字符串与后面的字符有相等的情况
假设S = "abcababca" T= "abcabx"

朴素算法
步骤1
S: a b c a b a b c a
T: a b c a b x
a 与 x 不匹配

步骤2
S: a b c a b a b c a
T: # a b c a b x
b 与 a 不匹配

步骤3
S: a b c a b a b c a
T: # # a b c a b x
c 与 a 不匹配

步骤4
S: a b c a b a b c a
T: # # # a b c a b x
a 与 a 匹配

步骤5
S: a b c a b a b c a
T: # # # # a b c a b x
b 与 b 匹配

步骤6
S: a b c a b a b c a
T: # # # # a b c a b x
a 与 c 不匹配

因为步骤1 中已经得出 前五位已经完全匹配 并且子串首字符ab 存在相同的情况 所以 步骤2，3 是多余的

直接进入步骤4 因为步骤1中已经得出 主串与子串前五位相同 同时 子串1 2 位与 子串的4 5 位相同 所以可得出
子串1 2 位 与当前主串匹配位置开始的前两位也就是主串的4 5 位匹配 所以步骤4 , 5 是多余的 可以直接进入步骤6

通过上面的两个例子我们可以发现 主串的比较位是不会回溯的 ， 而子串的比较位与子串本身结构中是否有重复相关

子串不重复 举例
S: a b c d e f g a
T: a b c d e x

子串第6位不匹配 且本身没有重复 那么下一次循环 就变成了 子串的第一位与主串的第二位比较
即子串的匹配位从6 变成了1

S: a b c d e f g a
T: # a b c d e x

子串重复 举例
S: a b c a b a b c a
T: a b c a b x
a 与 x 不匹配

子串在第六位发生不匹配是 前五位abcab 具有重复结构 ab 所以子串匹配位发生变化 即子串的匹配位从6 变成了 3

S: a b c a b a b c a
T: # # # a b c a b x
a 与 c 不匹配

我们可以得出 子串匹配位的值 与主串无关 只取决于当前字符串之前的串前后缀的相似度
也就是说 我们在查找字符前 ，要先对子串做一个分析 获取各个位置不匹配时 下一步子串的匹配位

前缀 ： 从头开始数 不包含最后一位
后缀 : 不是倒着数 是以和前缀相同的字符串为结尾的部分
例如 字符串 a 没有前后缀
字符串 ab 没有前后缀
字符串 aba 没有前后缀
字符串 abab 前后缀 ab
字符串 ababa 前后缀 可以是 a 可以是 aba 我们取长度最长的 即 aba

第一位时 next值固定为0
其他情况 取其公共最长前后缀的长度+1 没有则为1

因为一共子串有8位 所以在子循环内一共需要获取 8次前后缀
这里我们定义一个next数组 长度为8 里面的元素分别对应子串各个子循环内的 前后缀长度
第1位不匹配时 获取字符串为a 没有前字符串 没有前后缀 那么next[1] = 0
第2位不匹配时 获取字符串为ab 有前字符串a 没有前后缀 那么next[2] = 1
第3位不匹配时 获取字符串为aba 有前字符串ab 没有前后缀 那么next[3] = 1
第4位不匹配时 获取字符串为abab 有前字符串aba 前后缀 a 那么next[4] = 2
第5位不匹配时 获取字符串为ababa 有前字符串abab 前后缀 ab 那么next[5] = 3
第6位不匹配时 获取字符串为ababaa 有前字符串ababa 前后缀 aba 那么next[6] = 4
第7位不匹配时 获取字符串为ababaab 有前字符串ababaa 前后缀 a 那么next[7] = 2
第8位不匹配时 获取字符串为ababaabc 有前字符串ababaab 前后缀 ab 那么next[8] = 3

next数组为[ 0, 1 , 1 ,2 , 3, 4 ,2, 3 ]

后来有人发现 KMP还是有缺陷的 比如 当子串 T = "aaaaax"
在5位发生不匹配 此时 next[5] = 4 接着就是 子串中的第四位a与 主串当前位置字符比较

因为子串第五位等于子串第四位相同 所以可以得出该步骤也不匹配 此时 next[4] = 3
依然不匹配 直到next[1] = 0

我们可以发现由于T串中的 2 3 4 5 位置都与首位a 相等 中间的过程都是多余的
那么可以用首位的next[1] 的值 去替代与它相等的字符后续的next[x]的值

串的模式匹配算法之kmp

---

title: 串的模式匹配算法之kmp

tags: 数据结构与算法之美

author: 辰砂

---

1.引言

首先我们需要了解串的模式算法目的：确定主串中所含子串第一次出现的位置（定位）；常见的算法种类： BF算法（又称古典的、经典的、朴素的、穷举的），KMP算法（特点：速度快）。网上有很多帖子，博客写的都特别好，这篇文章也是对自己的一个总结。

2.BF算法

BF算法设计思想：

---

将主串的第pos个字符和模式的第一个字符比较
若相等，继续逐个比较后续字符；
若不等，从主串的下一字符起，重新与模式的第一个字符比较。
直到主串的一个连续子串字符序列与模式相等 。
返回值为S中与T匹配的子序列第一个字符的序号，即匹配成功。
否则，匹配失败，返回值 0

---

1.举例：

假设现在我们面临这样一个问题：有一个文本串S，和一个模式串P，现在要查找P在S中的位置，怎么查找呢？

 

如果用暴力匹配的思路，并假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置，则有：

如果当前字符匹配成功（即S[i] == P[j]），则i++，j++，继续匹配下一个字符；

如果失配（即S[i]! = P[j]），令i = i - (j - 1) （表示主串的位置回到当前的下一个位置），j = 0。相当于每次匹配失败时，i 回溯，j 被置为0。

1. public static int bfMatch(char[] s, char[] p) {
   int sLen = s.length;
   int pLen = p.length;
   int i = 0;
   int j = 0;
   while (i < sLen && j < pLen) {
   if (s[i] == p[j]) {
   //①如果当前字符匹配成功（即S[i] == P[j]），则i++，j++
   i++;
   j++;
   } else {
   //②如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0
   // i - (j - 1) 表示主串的位置回到当前的下一个位置。
   i = i - j + 1;
   j = 0;
   }
   }
   //匹配成功，返回模式串p在文本串s中的位置，否则返回-1
   if (j == pLen) {
   return i - j;
   } else {
   return -1;
   }
   }
   public static void main(String[] args) {
   String s = "BBC ABCDAB ABCDABCDABDE";
   String p = "ABCDABD";
   System.out.println(bfMatch(s.toCharArray(),p.toCharArray()));
   }

    

2.时间复杂度说明：

若n为主串长度，m为子串长度，最坏情况是 主串前面n-m个位置都部分匹配到子串的最后一位，即这n-m位各比较了m次 最后m位也各比较了1次

总次数为：(n-m)m+m＝(n-m+1)m 若m<<n，则算法复杂度o(n*m)< p="">

网上有个很好的例子，故引用：

举个例子，如果给定文本串S“BBC ABCDAB ABCDABCDABDE”，和模式串P“ABCDABD”，现在要拿模式串P去跟文本串S匹配，整个过程如下所示：

1.S[0]为B，P[0]为A，不匹配，执行第②条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[1]跟P[0]匹配，相当于模式串要往右移动一位（i=1，j=0）

2.S[1]跟P[0]还是不匹配，继续执行第②条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[2]跟P[0]匹配（i=2，j=0），从而模式串不断的向右移动一位（不断的执行“令i = i - (j - 1)，j = 0”，i从2变到4，j一直为0）

3.直到S[4]跟P[0]匹配成功（i=4，j=0），此时按照上面的暴力匹配算法的思路，转而执行第①条指令：“如果当前字符匹配成功（即S[i] == P[j]），则i++，j++”，可得S[i]为S[5]，P[j]为P[1]，即接下来S[5]跟P[1]匹配（i=5，j=1）

4.S[5]跟P[1]匹配成功，继续执行第①条指令：“如果当前字符匹配成功（即S[i] == P[j]），则i++，j++”，得到S[6]跟P[2]匹配（i=6，j=2），如此进行下去

5.直到S[10]为空格字符，P[6]为字符D（i=10，j=6），因为不匹配，重新执行第②条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，相当于S[5]跟P[0]匹配（i=5，j=0）

6.至此，我们可以看到，如果按照暴力匹配算法的思路，尽管之前文本串和模式串已经分别匹配到了S[9]、P[5]，但因为S[10]跟P[6]不匹配，所以文本串回溯到S[5]，模式串回溯到P[0]，从而让S[5]跟P[0]匹配。

而S[5]肯定跟P[0]失配。为什么呢？因为在之前第4步匹配中，我们已经得知S[5] = P[1] = B，而P[0] = A，即P[1] != P[0]，故S[5]必定不等于P[0]，所以回溯过去必然会导致失配。那有没有一种算法，让i 不往回退，只需要移动j 即可呢？

3.KMP算法（主串指针不回溯）

算法思想：利用已经部分匹配的结果而加快模式串的滑动速度？且主串S的指针i不必回溯！可提速到O(n+m)！

算法步骤： 下面先直接给出KMP的算法流程：

---

假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置

 

如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；

 

如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位。

 

换言之，当匹配失败时，模式串向右移动的位数为：失配字符所在位置 - 失配字符对应的next 值（next 数组的求解会在下文的3.3.3节中详细阐述），即移动的实际位数为：j - next[j]，且此值大于等于1。

 

---

很快，你也会意识到next 数组各值的含义：代表当前字符之前的字符串中，有多大长度的相同前缀后缀。例如如果next [j] = k，代表j 之前的字符串中有最大长度为k 的相同前缀后缀。

此也意味着在某个字符失配时，该字符对应的next 值会告诉你下一步匹配中，模式串应该跳到哪个位置（跳到next [j] 的位置）。如果next [j] 等于0或-1，则跳到模式串的开头字符，若next [j] = k 且 k > 0，代表下次匹配跳到j 之前的某个字符，而不是跳到开头，且具体跳过了k 个字符。

public static int kmpMatch(char[] s, char[] p) {
int sLen = s.length;
int pLen = p.length;
int i = 0;
int j = 0;
while (i < sLen && j < pLen) {
if (s[i] == p[j]) {
//①如果当前字符匹配成功（即S[i] == P[j]），则i++，j++
i++;
j++;
} else {
j = next[j];
}
}
//匹配成功，返回模式串p在文本串s中的位置，否则返回-1
if (j == pLen) {
return i - j;
} else {
return -1;
}
}

 

为此,定义next[j]函数，表明当模式中第j个字符与主串中相应字符“失配”时，在模式中需重新和主串中该字符进行比较的字符的位置。

1.如何求next()?

1.寻找前缀后缀最长公共元素长度

比如 字符串 ‘a’ 的前缀就是为空，后缀也是为空，所以前缀后缀的意思，是不包括当前字符串，字符串 ‘ab’ 的前缀是a，后缀是b。

定义： 对于P = p0 p1 ...pj-1 pj，寻找模式串P中长度最大且相等的前缀和后缀。如果存在p0 p1 ...pk-1 pk = pj- k pj-k+1...pj-1 pj，那么在包含pj的模式串中有最大长度为k+1的相同前缀后缀。

比如：

j	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
模式串	a	b	c	a	a	b	c	a	b	c	a	a	a	b	d	a	b
前后缀最长公共元素	0	0	0	1	1	2	3	1	2	3	4	5	6	2	0	1	2

 

 

 

2.求next数组

next 数组考虑的是除当前字符外的最长相同前缀后缀，所以通过第①步骤求得各个前缀后缀的公共元素的最大长度后，只要稍作变形即可：将第①步骤中求得的值整体右移一位，然后初值赋为-1，如下表格所示：

j	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
模式串	a	b	c	a	a	b	c	a	b	c	a	a	a	b	d	a	b
next[j]	0	1	1	1	2	2	3	1	1	2	3	4	5	6	2	1	2

 

 

 

 

 

 

3.如何求next函数值

1. next[1] = 0;表明主串从下一字符si+1起和模式串重新开始匹配。i = i+1; j = 1;

    

2. 设next[j] = k，则next[j+1] = ?

    

   ①若pk=pj，则有“p1…pk-1pk”=“pj-k+1…pj-1pj” ，如果在 j+1发生不匹配，说明next[j+1] = k+1 = next[j]+1。

    

   ②若pk≠pj，可把求next值问题看成是一个模式匹配问 题，整个模式串既是主串，又是子串。

    

   

若pk’=pj，则有“p1…pk’”=“pj-k’+1…pj”， next[j+1]=k’+1=next[k]+1=next[next[j]]+1.

若pk”=pj ，则有“p1…pk””=“pj-k”+1…pj”， next[j+1]=k”+1=next[k’]+1=next[next[k]]+1. next[j+1]=1.

 

 

4.总结

核心的点在于：以前的bf算法是需要i进行回溯，导致时间复杂度O(m*n) ,现在kmp算法的核心是i不进行回溯，而j这个值不确定，根据串的规律，主串前面匹配成功的串前缀和后缀相等的地方不需要匹配即可。这样的时间复杂度是O(m + n)

引用博客例子：

1.最开始匹配时

P[0]跟S[0]匹配失败

 

所以执行“如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]”，所以j = -1，故转而执行“如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++”，得到i = 1，j = 0，即P[0]继续跟S[1]匹配。

 

P[0]跟S[1]又失配，j再次等于-1，i、j继续自增，从而P[0]跟S[2]匹配。

 

P[0]跟S[2]失配后，P[0]又跟S[3]匹配。

 

P[0]跟S[3]再失配，直到P[0]跟S[4]匹配成功，开始执行此条指令的后半段：“如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++”。

 

 

2.P[1]跟S[5]匹配成功，P[2]跟S[6]也匹配成功, ...，直到当匹配到P[6]处的字符D时失配（即S[10] != P[6]），由于P[6]处的D对应的next 值为2，所以下一步用P[2]处的字符C继续跟S[10]匹配，相当于向右移动：j - next[j] = 6 - 2 =4 位。

3.向右移动4位后，P[2]处的C再次失配，由于C对应的next值为0，所以下一步用P[0]处的字符继续跟S[10]匹配，相当于向右移动：j - next[j] = 2 - 0 = 2 位。

4.移动两位之后，A 跟空格不匹配，模式串后移1 位。

5.P[6]处的D再次失配，因为P[6]对应的next值为2，故下一步用P[2]继续跟文本串匹配，相当于模式串向右移动 j - next[j] = 6 - 2 = 4 位。

6.匹配成功，过程结束。

匹配过程一模一样。也从侧面佐证了，next 数组确实是只要将各个最大前缀后缀的公共元素的长度值右移一位，且把初值赋为-1 即可。

代码如下：

void get_next(SString T, int &next[])
{
i= 1; next[1] = 0; j = 0;
while( i<T[0]){
if(j==0 || T[i] == T[j]){
++i; ++j;
next[i] = j;
}
else
j = next[j];
}
}

 

kMP算法的时间复杂度

设主串s的长度为n,模式串t长度为m,在KMP算法中求next数组的时间复杂度为O(m),在后面的匹配中因主串s的下标不减即不回溯,比较次数可记为n,所以KMP算法总的时间复杂度为O(n+m)

---

参考原文：https://blog.csdn.net/vjulyv/article/details/7041827?utm_source=copy