GBDT原理详解及sklearn源码解析

Posted 2023-04-13

参考技术A 以下关于GBM和GBDT的理解来自经典论文[greedy function approximation: a gradient boosting machine]，by Jerome H.Friedman,( https://github.com/LouisScorpio/datamining/tree/master/papers )

论文的整体思路：
1.函数空间的数值优化
对算法中损失函数的数值优化不是在参数空间，而是在函数空间，数值优化方式为梯度下降；
2.GBM
以加法模型为基础，使用上述优化方法，构建一套通用梯度提升算法GBM；
3.不同损失类型的GBM
具体展现使用不同类型的损失时的GBM；
4.GBDT
以CART回归树为加法模型的弱分类器，构建算法模型即GBDT。

首先，考虑加法模型，即最终分类器是由多个弱分类器线性相加的结果，表示为以下形式：
           (1)
其中，h(x;a)是弱分类器，是关于输入特征x的函数，a是函数的参数（如果h(x;a)为回归树，那么a就是回归树中用于分裂的特征、特征的分裂点以及树的叶子节点的分数），M是弱分类器的数量， 为弱分类器的权重（在GBDT中相当于learning_rate，即起到shrinkage的作用）。

假设预测的目标函数为F(x; P)，其中P为参数，损失为L，那么损失函数表示为：
        
对应参数P的最优解表示为：
          
考虑使用梯度下降的优化方式，首先计算损失函数 对参数P的梯度 :
         
然后，对参数P沿着负梯度方向即- 方向更新，更新的步长为：
           
其中 是在负梯度方向上更新参数的最优步长，通过以下方式线性搜索得到：
       
从初始值 开始，经过多次这样的更新迭代之后，参数P的值最终为：
        
以上为参数空间的数值优化。

在函数空间，假设预测的目标函数为F(x)，损失为L，那么损失函数表示为：
        
注意，这里损失函数的参数不再是P，而是函数 。
按照梯度下降的优化方式，这里要计算损失函数 对函数F的梯度 :
     
然后对函数沿着负梯度方向更新，更新的步长如下：
         
其中 是在负梯度方向上更新参数的最优步长，通过以下方式线性搜索得到：
   
经过多次迭代之后，最终的函数结果为：
         

考虑（1）中的加法模型形式，可以得到
      
假设损失为L，那么
 
根据函数空间的数值优化， 应该对应于负梯度：
    
在模型训练时，负梯度 是基于样本点进行的估计，为了提高泛化能力，一种可行的解决办法是让 去拟合负梯度 ，由此得到：
    
拟合学习到的 作为加法模型的弱学习器。加法模型的步长通过线性搜索的方式得到：
  
综上，GBM整个算法流程如下：

对抗生成网络GAN系列——Spectral Normalization原理详解及源码解析

🍊作者简介：秃头小苏，致力于用最通俗的语言描述问题

🍊专栏推荐：深度学习网络原理与实战

🍊近期目标：写好专栏的每一篇文章

🍊支持小苏：点赞👍🏼、收藏⭐、留言📩

 

对抗生成网络GAN系列——Spectral Normalization原理详解及源码解析

写在前面

Hello，大家好，我是小苏🧒🏽🧒🏽🧒🏽

在前面的文章中，我已经介绍过挺多种GAN网络了，感兴趣的可以关注一下我的专栏：深度学习网络原理与实战 。目前专栏主要更新了GAN系列文章、Transformer系列和语义分割系列文章，都有理论详解和代码实战，文中的讲解都比较通俗易懂，如果你希望丰富这方面的知识，建议你阅读试试，相信你会有蛮不错的收获。🍸🍸🍸

在阅读本篇教程之前，你非常有必要阅读下面两篇文章：

• [1]对抗生成网络GAN系列——DCGAN简介及人脸图像生成案例
• [2]对抗生成网络GAN系列——WGAN原理及实战演练

其实啊，我相信大家来看这篇文章的时候，一定是对上文提到的文章有所了解了，因此大家要是觉得自己对GAN和WGAN了解的已经足够透彻了，那么完全没有必要再浪费时间阅读了。如果你还对它们有一些疑惑或者过了很久已经忘了希望回顾一下的话，那么文章[1]和文章[2]获取对你有所帮助。

大家准备好了嘛，我们这就开始准备学习Spectral Normalization啦！🚖🚖🚖

 

Spectral Normalization原理详解

​  首先，让我们简单的回顾一下WGAN。🌞🌞🌞由于原始GAN网络存在训练不稳定的现象，究其本质，是因为它的损失函数实际上是JS散度，而JS散度不会随着两个分布的距离改变而改变（这句不严谨，细节参考WGAN中的描述），这就会导致生成器的梯度会一直不变，从而导致模型训练效果很差。WGAN为了解决原始GAN网络训练不稳定的现象，引入了EM distance代替原有的JS散度，这样的改变会使生成器梯度一直变化，从而使模型得到充分训练。但是WGAN的提出伴随着一个难点，即如何让判别器的参数矩阵满足Lipschitz连续条件。

​  如何解决上述所说的难点呢？在WGAN中，我们采用了一种简单粗暴的方式来满足这一条件，即直接对判别器的权重参数进行剪裁，强制将权重限制在[-c,c]范围内。大家可以动动我们的小脑瓜想想这种权重剪裁的方式有什么样的问题——（滴，揭晓答案🍍🍍🍍）如果权重剪裁的参数c很大，那么任何权重可能都需要很长时间才能达到极限，从而使训练判别器达到最优变得更加困难；如果权重剪裁的参数c很小，这又容易导致梯度消失。因此，如何确定权重剪裁参数c是重要的，同时这也是困难的。WGAN提出之后，又提出了WGAN-GP来实现Lipschitz 连续条件，其主要通过添加一个惩罚项来实现。【关于WGAN-GP我没有做相关教程，如果不明白的可以评论区留言】那么本文提出了一种归一化的手段Spectral Normalization来实现Lipschitz连续条件，这种归一化具体是怎么实现的呢，下面听我慢慢道来。🍻🍻🍻

---

我们还是来先回顾一下Lipschitz连续条件，如下：

​            $$|f(x_1)-f(x_2)|\le K|x_1-x_2|$$

这个式子限制了函数$\mathrm{f}(\cdot )$的导数，即其导数的绝对值小于K，$\frac{|f(x_1)-f(x_2)|}{|x_1-x_2|}\le K$。 🍋🍋🍋

本文介绍的Spectral Normalization的K=1，让我们一起来看看怎么实现的吧！！！

---

  上文提到，WGAN的难点是如何让判别器的参数矩阵满足Lipschitz连续条件。那么我们就从判别器入手和大家唠一唠。实际上，判别器也是由多层卷积神经网络构成的，我们用下式表示第n层网络输出和第n-1层输入的关系：

​            $$X_n=a_n(W_n\cdot X_{n-1}+b_n)$$

  其中$a_n(\cdot )$表示激活函数，$W_n$表示权重参数矩阵。为了方便起见，我们不设置偏置项$b_n$，即$b_n=0$。那么上式变为：

​            $$X_n=a_n(W_n\cdot X_{n-1})$$

  再为了方便起见🤸🏽‍♂️🤸🏽‍♂️🤸🏽‍♂️，我们设$a_n(\cdot )$，即激活函数为Relu。Relu函数在大于0时为y=x，小于0时为y=0，函数图像如下图所示：

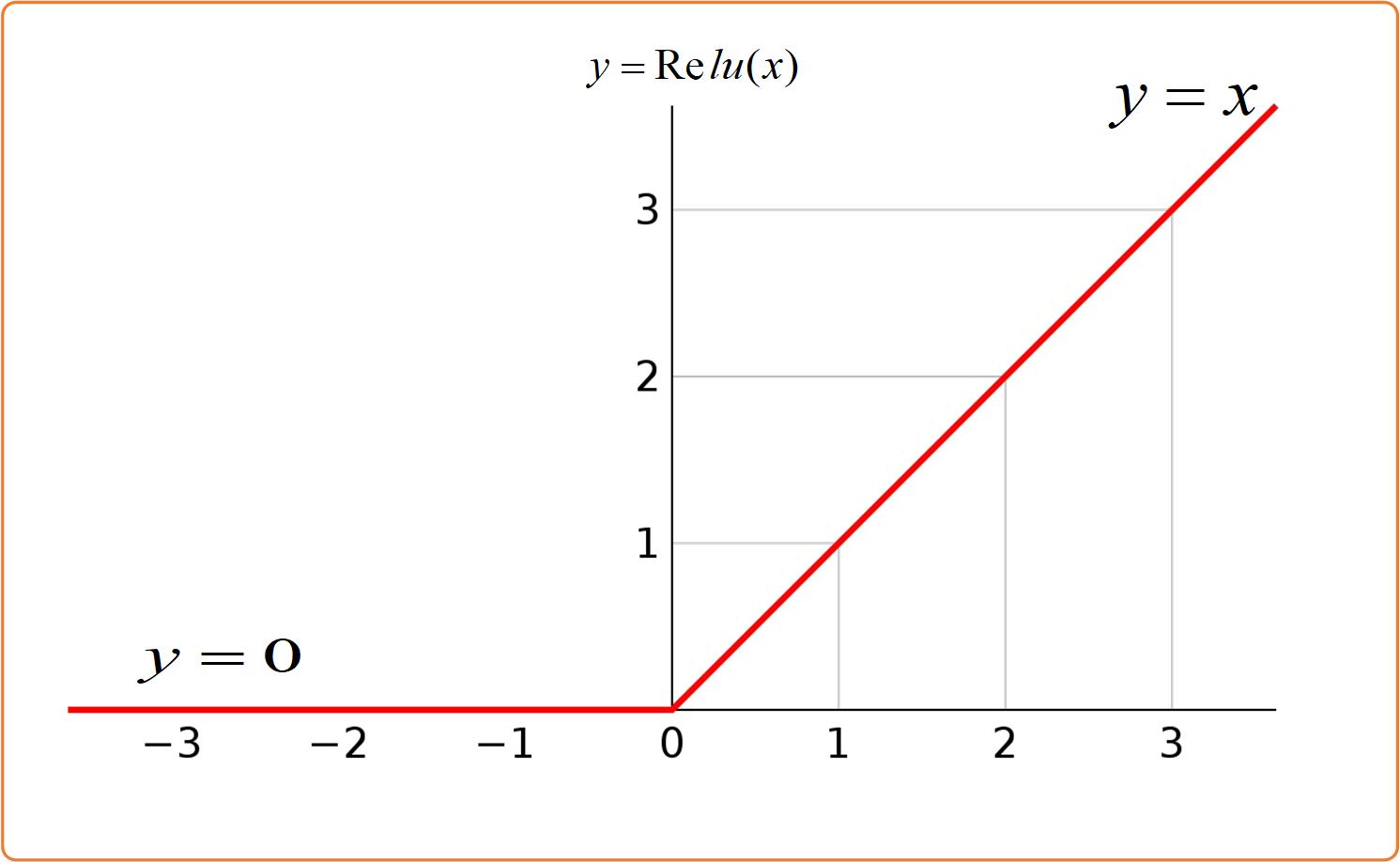
​  这样的话式$X_n=a_n(W_n\cdot X_{n-1})$可以写成$X_n=D_n\cdot W_n\cdot X_{n-1}$，其中$D_n$为对角矩阵。【大家这里能否理解呢？如果我们的输入为正数时，通过Relu函数值是不变的，那么此时$D_n$对应的对角元素应该为1；如果我们的输入为负数时，通过Relu函数值将变成0，那么此时$D_n$对应的对角元素应该为0。也就是说我们将$X_n$改写成$D_n\cdot W_n\cdot X_{n-1}$形式是可行的。】

​  接着我们做一些简单的推理，得到判别器第n层输出和原始输入的关系，如下图所示：

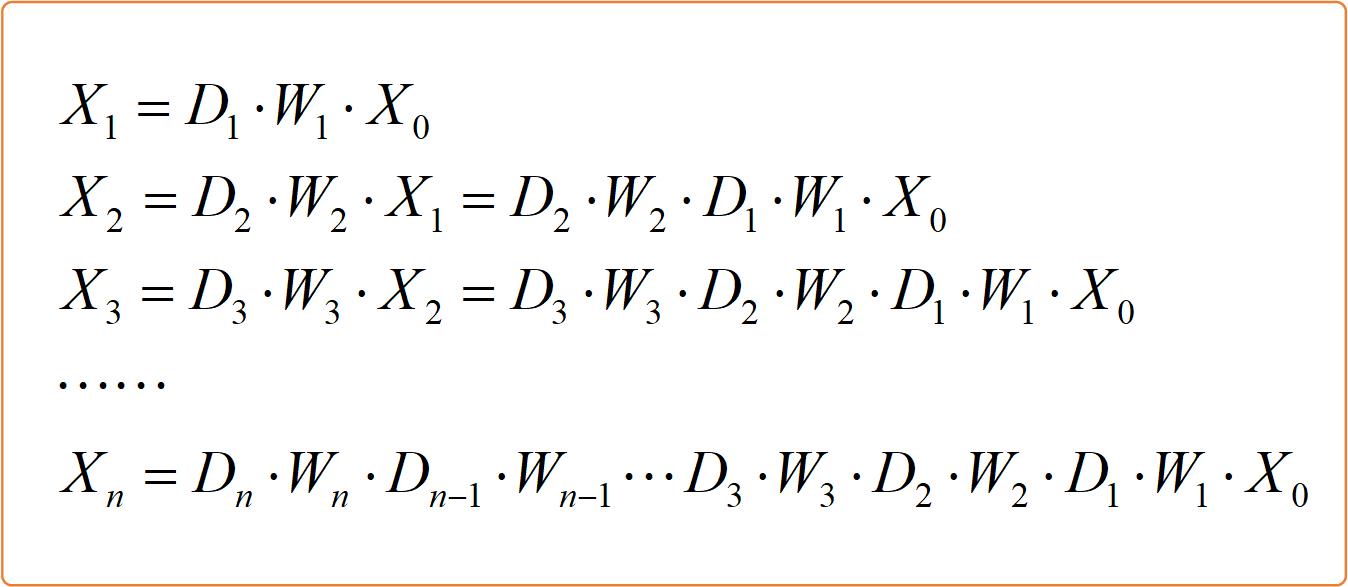
  最后一层的输出$X_n$即为判别器的输出，接下来我们用$f(x)$表示；原始输入数据$x_0$我们接下来用$x$表示。则判别器最终输入输出的关系式如下：

​   $$f(x)=D_n\cdot W_n\cdot D_{n-1}\cdot W_{n-1}\cdots D_3\cdot W_3\cdot D_2\cdot W_2\cdot D_1\cdot W_1\cdot x$$

  上文说到Lipschitz连续条件本质上就是限制函数$\mathrm{f}(\cdot )$的导数变化范围，其实就是对$f(x)$梯度提出限制，如下：

∣ ∣ ∇ x f ( x ) ∣ ∣ 2 = ∣ ∣ D n ⋅ W n ⋅ D n − 1 ⋅ W n − 1 ⋯ D 3 ⋅ W 3 ⋅ D 2 ⋅ W 2 ⋅ D 1 ⋅ W 1 ∣ ∣ 2 ≤ ∣ ∣ D n ∣ ∣ 2 ⋅ ∣ ∣ W n ∣ ∣ 2 ⋅ ∣ ∣ D n −