JS实现最短路径之弗洛伊德(Floyd)算法

Posted 2021-01-20 追风逐月

　　弗洛伊德算法是实现最小生成树的一个很精妙的算法，也是求所有顶点至所有顶点的最短路径问题的不二之选。时间复杂度为O(n3)，n为顶点数。

　　精妙之处在于：一个二重初始化，加一个三重循环权值修正，完成了所有顶点至所有顶点的的最短路径计算，代码及其简洁

 

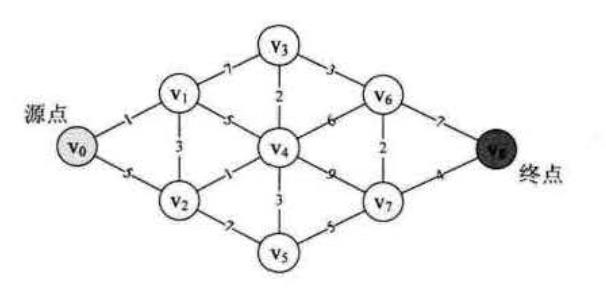
JS实现：

//定义邻接矩阵
let Arr2 = [
    [0, 1, 5, 65535, 65535, 65535, 65535, 65535, 65535],
    [1, 0, 3, 7, 5, 65535, 65535, 65535, 65535],
    [5, 3, 0, 65535, 1, 7, 65535, 65535, 65535],
    [65535, 7, 65535, 0, 2, 65535, 3, 65535, 65535],
    [65535, 5, 1, 2, 0, 3, 6, 9, 65535],
    [65535, 65535, 7, 65535, 3, 0, 65535, 5, 65535],
    [65535, 65535, 65535, 3, 6, 65535, 0, 2, 7],
    [65535, 65535, 65535, 65535, 9, 5, 2, 0, 4],
    [65535, 65535, 65535, 65535, 65535, 65535, 7, 4, 0],
]

let numVertexes = 9, //定义顶点数
    numEdges = 15; //定义边数

// 定义图结构  
function MGraph() {
    this.vexs = []; //顶点表
    this.arc = []; // 邻接矩阵，可看作边表
    this.numVertexes = null; //图中当前的顶点数
    this.numEdges = null; //图中当前的边数
}
let G = new MGraph(); //创建图使用

//创建图
function createMGraph() {
    G.numVertexes = numVertexes; //设置顶点数
    G.numEdges = numEdges; //设置边数

    //录入顶点信息
    for (let i = 0; i < G.numVertexes; i++) {
        G.vexs[i] = \'V\' + i; //scanf(\'%s\'); //ascii码转字符 //String.fromCharCode(i + 65);
    }
    console.log(G.vexs) //打印顶点

    //邻接矩阵初始化
    for (let i = 0; i < G.numVertexes; i++) {
        G.arc[i] = [];
        for (j = 0; j < G.numVertexes; j++) {
            G.arc[i][j] = Arr2[i][j]; //INFINITY; 
        }
    }
    console.log(G.arc); //打印邻接矩阵
}

let Pathmatirx = []; //二维数组 表示顶点到顶点的最短路径权值和的矩阵
let ShortPathTable = []; //二维数组 表示对应顶点的最小路径的前驱矩阵

function Floyd() {

    let w, k;
    for (let v = 0; v < G.numVertexes; ++v) { //初始化 Pathmatirx ShortPathTable
        Pathmatirx[v] = [];
        ShortPathTable[v] = [];
        for (let w = 0; w < G.numVertexes; ++w) {
            ShortPathTable[v][w] = G.arc[v][w];
            Pathmatirx[v][w] = w;
        }
    }

    for (let k = 0; k < G.numVertexes; ++k) {
        for (let v = 0; v < G.numVertexes; ++v) {
            for (let w = 0; w < G.numVertexes; ++w) {
                if (ShortPathTable[v][w] > (ShortPathTable[v][k] + ShortPathTable[k][w])) {
                    //如果经过下标为k顶点路径比原两点间路径更短，当前两点间权值设为更小的一个
                    ShortPathTable[v][w] = ShortPathTable[v][k] + ShortPathTable[k][w];
                    Pathmatirx[v][w] = Pathmatirx[v][k]; //路径设置经过下标为k的顶点
                }
            }
        }
    }
}

function PrintAll() {
    for (let v = 0; v < G.numVertexes; ++v) {
        for (let w = v + 1; w < G.numVertexes; w++) {
            console.log(\'V%d-V%d weight: %d\', v, w, ShortPathTable[v][w]);
            k = Pathmatirx[v][w];
            console.log(\' Path: %d\', v);
            while (k != w) {
                console.log(\' -> %d\', k);
                k = Pathmatirx[k][w];
            }
            console.log(\' -> %d\', w);
        }
    }
}

createMGraph();
Floyd();
PrintAll();

运行结果：（结果太长只截取不分）

 

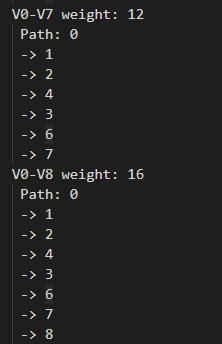
求最短路径的两个算法（迪杰斯特拉算法和弗洛伊德算法），对有向图依然有效，因为二者的差异仅仅是邻接矩阵是否对称而已

 

参考文献： 程杰 《大话设计模式》