九大行星绕日运行的周期? 九大行星绕日运行的周期,公转自转各是多久?

Posted 2023-04-11

参考技术A 天王星基本数据 质量:8.686×1025 千克 赤道半径:25559千米 平均密度:1.29克/厘米3 表面平均温度:59K 表面重力加速度(赤道):7.77厘米/秒2 自转周期:17.9小时 赤道面和轨道面交角:97.86° 轨道半长径:19.1914天文单位 公转周期:84.01年 轨道偏心率:0.0461 轨道倾角:0.774° 木星的带纹 木星在众行星中有着突出的特点：质量大、体积大.它的质量是太阳系中其它8颗行星加在一起的二倍半,相当于地球的1316倍.如果把地球和木星放在一起,就如同芝麻和西瓜之比一样悬殊.木星虽然巨大无比,但它的自转速度却是太阳系中最快的.自转周期为9小时50分30秒.土星简介 土星是离太阳第六远的一颗美丽的行星,凡是用望远镜看过土星的人,无不惊叹不已.土星公转轨道半径为14亿千米,冲日时最大亮度为0.4星等.土星那橘色的表面,漂浮着明暗相间的彩云,配以赤道面上那发出柔和光辉的光环,远远望去真像个戴着顶大沿遮阳帽的女郎.要比两极半径大6000多千米.土星公转周期为29.5年,约合二十八宿之数,每年镇一宿,故古时我国又称其为“镇星”.地球基本数据 赤道半径 6378140米 扁率因子 298.257 质量 5.976×1027克 平均密度 5.52克/厘米3 表面重力加速度(赤道) 978.0厘米/秒2 表面重力加速度(极地) 983.2厘米/秒2 自转周期 23时56分4秒(平太阳时) 公转轨道半长径 149597870千米 公转轨道偏心率 0.0167 公转周期 1恒星年 黄赤交角 23度27分 金星自转周期是243天,比公转周期(224.7天)还长.金星上的一昼夜相当于地球上的117天.在一个金星年中,金星上只能看到两次太阳西升东落.水星在绕太阳公转的同时,本身也在自转.1889年,意大利天文学家夏帕里利经过对水星多年的观测,认为水星自转一周的时间和公转一周的时间都是88天.对此,人们一直深信不疑.1965年,美国天文学家佩廷吉尔和戴斯,借助美国阿雷西沃(Arecibo)天文台的世界最大的射电望远镜,测量了水星两个边缘反射波间的频率差,成功地测量了水星的自转周期为58.646日,正好是水星公转周期的2／3.地球每自转一周就是一昼夜,而水星自转三周才是一昼夜.水星上一昼夜的时间,相当于地球上的176天.与此同时,水星也正好公转了两周.因此人们说水星上的一天等于两年.由于水星在近日点时总以同一经度朝着太阳,在远日点时以相差90°的经度朝着太阳,所以水星随着经度不同而出现季节变化.

Scratch编程：牛顿的苹果——地心引力

牛顿的苹果

同学们，你们知道牛顿的苹果的故事吗？

传说1665年秋季，牛顿坐在自家院中的苹果树下苦思着行星绕日运动的原因。这时，一只苹果恰巧落下来，它落在牛顿的脚边。就是这个偶尔的瞬间，牛顿发现了苹果下落的原因——地心引力的作用。

从此，这个苹果被视为科学探索精神的象征。那么，同学们，我们也来探索一下，我们在Scratch中，如何模拟物体的下落？

就像牛顿发现了苹果下落的道理一下，我们需要对于重力的效果进行模拟从而制作出来下落的过程。

对于简单的程序，可使用均速下降的方式。即每隔一段进行将Y坐标增加一个固定的值，就可以了。

对于一些要求比较高的程序，需要使用算法来进行比较准确的模拟。

 

在重力的作用下运动，一般称为自由落体。根据物理学的知识，物体从0速度开始的自由落体，使用如下的公式进行描述：

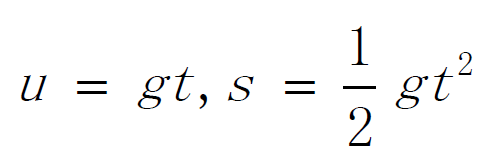
式中的t为时间，一般单位为秒； s为位移（或者说下降的距离）单位为米；u为速度，单位为米/秒; 其中的g为重力加速度,单位为米/秒^2，体现了重力对于自由落体的影响。在不同的星球上，重力加速度的数值是不同的。

在地球上，重力加速度的数值约为9.81米/秒^2，而在月球上，重力加速度的数值约为1.633米/秒^2。所以在月球上，自由落体的下落速度会比地球上慢得多。

我们再对上面的两个公式进行一点深入的解释。

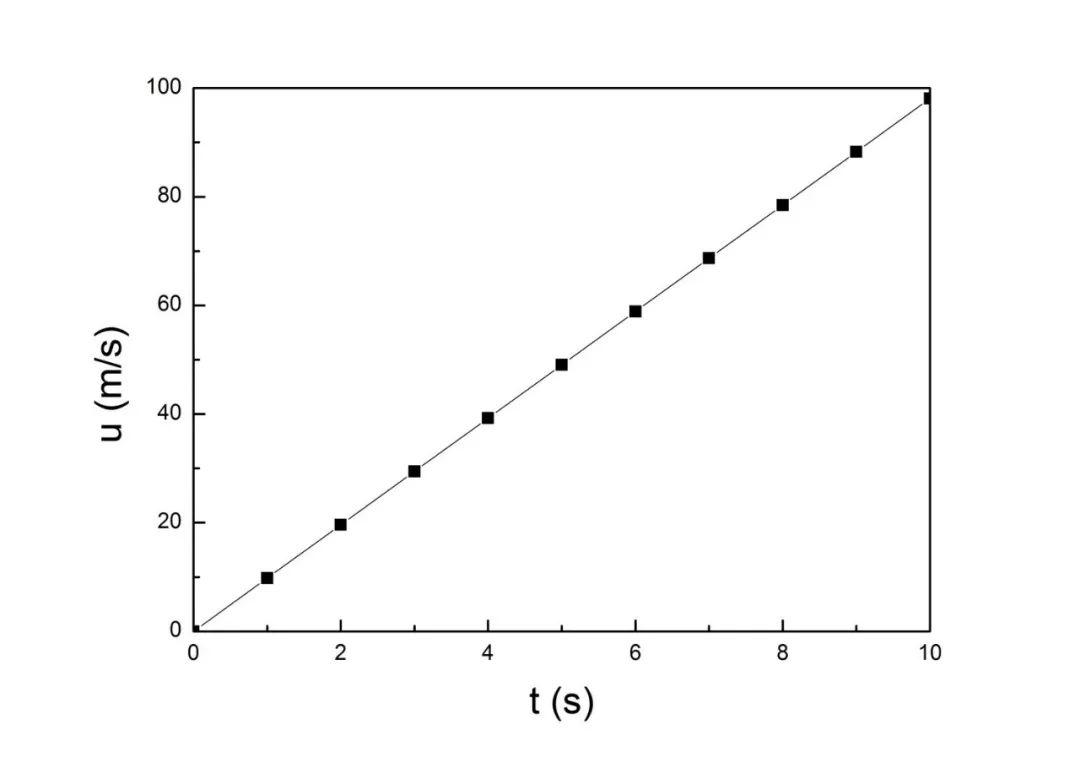
第一个公式表示了自由落体下降速度随时间的变化。也就是“速度＝时间*加速度”，所以物体在自由下落的过程中，速度会越来越快，而如果加速度大，则相同时间下速度变化得更大。

速度与时间之间是直线的关系。

而位移与时间的关系则是一条抛物线，可以看到随时间的增加，位移变化得越来越快。在1秒时，下降了4.9米，而在2秒时，已下降了19.6米。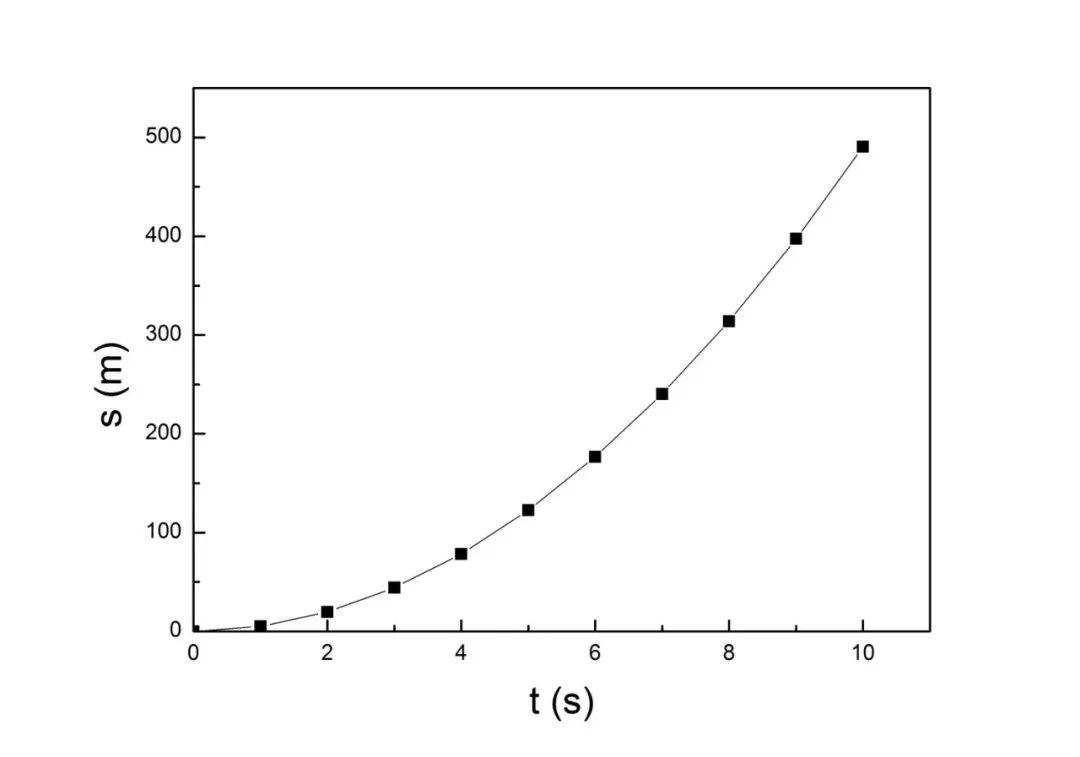

在我们的程序中，应该如何对重力进行模拟呢？

下面我们在Scratch中模拟一个小球的下落，来检查算法的正确性。

基本程序如下，放置一个小球。编写如下的程序。

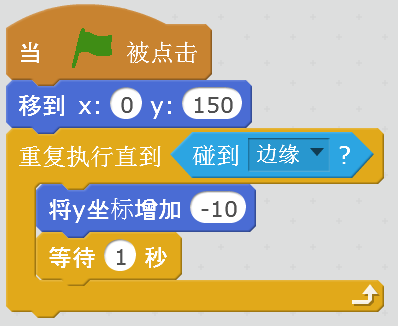
当然，上面这个程序是匀速下降的，下面我们对自由落体的加速过程进行模拟。

方法1：直接使用位移公式

结果如下，可以看到球运动得越来越快。如果改变时间的间隔，能够使得位置变化的更平滑一些。如果改变加速度g，就可以看到下降的速度会增快或减慢。

应该说明，这里直接使用下降的距离作为Y值的变化，即将一个像素当成了1米，可以看到10秒钟下降了397米，即397个像素。

方法2  考虑速度的变化

上面这种方法对于一次下落是很好的，但如果涉及到反弹等的模拟，还是需要考虑速度的变化。

这时使用的公式实际上是在每个时间的间隔Δt时，速度都增加g*Δt,而在同时，位移基本上变化Δt*u。这样就可以比较灵活地对抛物等进行模拟了。例如下面的程序就可以完成弹球的模拟。

其中tstep为时间间隔，xSpeed为X方向运行的速度，0.95表示每次反弹，速度都降为原来的0.95倍（模拟损失了能量）。

效果如下：

可以看到，模拟了自由落体的弹跳。

 

总结

 

 

 

结论：

 

1    模拟重力是很多程序中需要使用的功能。

2    根据自由落体的公式，给出了在SCRATCH中模拟自由落体的实现方式。

3    使用自由落体的算法，可以准确地模拟物体的下落过程及弹跳过程等。

4    数学和物理是进行程序模拟的基础，为了更好地对自然界进行模拟，学好数学和物理是必须的。