增量学习Contiual learning
Posted 翻身的咸鱼ing
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了增量学习Contiual learning相关的知识,希望对你有一定的参考价值。
下面是简单的EWC算法的代码,使用MNIST 数据集和USPS 数据集
import torch
import ssl
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
from torch.utils.data import DataLoader, random_split
# 禁用SSL验证
ssl._create_default_https_context = ssl._create_unverified_context
# Data preparation
transform = transforms.Compose([
transforms.Resize((28,28)),
transforms.ToTensor(),
#.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)) # 对所有通道进行归一化,使其分布在[-1, 1]范围内
])
# train_dataset = datasets.MNIST('./data', train=True, download=True, transform=transform)
#
# #task1_data = [data for data in train_dataset if data[1] < 5]
# #task2_data = [data for data in train_dataset if data[1] >= 5]
# # Split data into two groups
# train_dataset_size = len(train_dataset)
# train_split_sizes = [train_dataset_size // 2, train_dataset_size - train_dataset_size // 2]
# task1_data, task2_data = random_split(train_dataset, train_split_sizes)
#
#
#
# task1_loader = DataLoader(task1_data, batch_size=64, shuffle=True)
# task2_loader = DataLoader(task2_data, batch_size=64, shuffle=True)
#
# test_dataset = datasets.MNIST('./data', train=False, download=True, transform=transform)
#
# #task1_test_data = [data for data in test_dataset if data[1] < 5]
# #task2_test_data = [data for data in test_dataset if data[1] >= 5]
# test_dataset_size = len(test_dataset)
# test_split_sizes = [test_dataset_size // 2, test_dataset_size - test_dataset_size // 2]
# task1_test_data, task2_test_data = random_split(test_dataset, test_split_sizes)
#
# task1_test_loader = DataLoader(task1_test_data, batch_size=64, shuffle=False)
# task2_test_loader = DataLoader(task2_test_data, batch_size=64, shuffle=False)
# 加载 MNIST 数据集
task1_data = datasets.MNIST('./data', train=True, download=True, transform=transform)
task1_test_data = datasets.MNIST('./data', train=False, download=True, transform=transform)
task1_loader = DataLoader(task1_data , batch_size=64, shuffle=True)
task1_test_loader = DataLoader(task1_test_data, batch_size=64, shuffle=False)
# 加载 USPS 数据集
task2_data = datasets.USPS('./data', train=True, download=True, transform=transform)
task2_test_data = datasets.USPS('./data', train=False, download=True, transform=transform)
task2_loader = DataLoader(task2_data, batch_size=64, shuffle=True)
task2_test_loader = DataLoader(task2_test_data, batch_size=64, shuffle=False)
# Model definition
class SimpleNet(nn.Module):
def __init__(self):
super(SimpleNet, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
def forward(self, x):
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2(x), 2))
x = x.view(-1, 320)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
# EWC implementation
class EWC:
def __init__(self, model, dataloader, device, importance=1000):
self.model = model
self.importance = importance
self.device = device
self.params = n: p.clone().detach() for n, p in self.model.named_parameters() if p.requires_grad
self.fisher = self._compute_fisher(dataloader)
#计算fisher信息矩阵
def _compute_fisher(self, dataloader):
fisher =
for n, p in self.model.named_parameters():
if p.requires_grad:
fisher[n] = torch.zeros_like(p.data)
self.model.train()
for data, target in dataloader:
data, target = data.to(self.device), target.to(self.device)
self.model.zero_grad()
output = F.log_softmax(self.model(data), dim=1)
loss = F.nll_loss(output, target)
loss.backward()
for n, p in self.model.named_parameters():
if p.requires_grad:
fisher[n] += (p.grad ** 2) / len(dataloader)
return fisher
def penalty(self, new_model):
loss = 0
for n, p in new_model.named_parameters():
if p.requires_grad:
_loss = self.fisher[n] * (p - self.params[n]) ** 2
loss += _loss.sum()
return loss * (self.importance / 2)
# Train function
def train(model, dataloader, optimizer, criterion, device, ewc=None, ewc_lambda=0.5):
model.train()
for data, target in dataloader:
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = criterion(output, target)
if ewc is not None:
ewc_loss = ewc.penalty(model)
loss += ewc_lambda * ewc_loss
loss.backward()
optimizer.step()
# Test function
def test(model, dataloader, device):
model.eval()
correct = 0
total = 0
with torch.no_grad():
for data, target in dataloader:
data, target = data.to(device), target.to(device)
output = model(data)
_, predicted = torch.max(output.data, 1)
total += target.size(0)
correct += (predicted == target).sum().item()
accuracy = 100 * correct / total
return accuracy
# Device
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# Initialize model
model = SimpleNet().to(device)
# Train on Task 1
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
criterion = nn.CrossEntropyLoss()
for epoch in range(10):
train(model, task1_loader, optimizer, criterion, device)
task1_accuracy = test(model, task1_test_loader, device)
print(f'Task 1 accuracy: task1_accuracy%')
# Save EWC
ewc = EWC(model, task1_loader, device)
# Train on Task 2
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
for epoch in range(10):
train(model, task2_loader, optimizer, criterion, device, ewc=ewc, ewc_lambda=10 )
task2_accuracy = test(model, task2_test_loader, device)
print(f'Task 2 accuracy: task2_accuracy%')
# Train on Task 2 but don't have ewc
# optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
#
# for epoch in range(10):
# #训练ewc=none代表不使用ewc算法
# train(model, task2_loader, optimizer, criterion, device, ewc=None)
# task2_accuracy = test(model, task2_test_loader, device)
#
# print(f'Task 2 dont have ewc accuracy: task2_accuracy%')
task1_accuracy_new = test(model, task1_test_loader, device)
print(f'Tasknew 1 accuracy: task1_accuracy_new%')
task2_accuracy_NEW = test(model, task2_test_loader, device)
print(f'Tasknew 2 accuracy: task2_accuracy_NEW%')
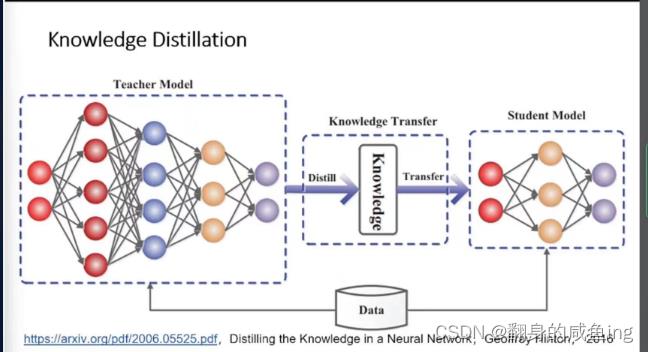
知识蒸馏
知识蒸馏就是有两个模型,一个训练好的Teacher模型一个没有训练Student模型,Student模型尽可能的学习到Teacher模型的知识。
软标签(Soft labels)是指模型输出的类别概率分布,其值通常在0到1之间,而且所有类别的概率之和为1。软标签与硬标签(Hard labels)相对应。硬标签是指具有单一类别的确定性标签,通常表示为一个整数或独热编码(One-Hot encoding)向量。
在神经网络中,当网络输出层的激活函数(如softmax)计算出每个类别的概率时,就可以得到软标签。与硬标签相比,软标签包含更多的信息,例如每个类别的置信度,这有助于模型更好地了解不同类别之间的关系。
在知识蒸馏中,软标签起着关键作用。教师网络为每个输入样本生成软标签,学生网络则试图学习这些软标签。通过学习软标签,学生网络可以捕捉到教师网络的潜在知识,从而提高其泛化能力。为了生成更有用的软标签,通常使用温度(Temperature)参数对教师网络的输出进行缩放。较高的温度值会使概率分布更平滑,从而使学生网络更容易捕捉到教师网络的知识。
当我们训练神经网络进行分类任务时,网络最终需要输出每个类别的概率值。在这之前,神经网络会将输入数据通过一系列数学运算和非线性变换,最终得到一个未经过 softmax 函数处理的向量。这个向量就是 logits。在 logits 中,每个元素对应一个类别,其值越大表示模型越认为这个样本属于这个类别,但这些值并不一定满足概率分布的要求(比如值域不在 [0,1] 区间内,且值的总和不一定为1)。因此,我们需要经过 softmax 函数的处理,将 logits 转换为一个概率分布,才能最终得到每个类别的概率值。简单来说,logits 就是神经网络分类任务中未经过处理的输出结果,通过 softmax 函数的处理后,我们才能得到具有概率意义的输出。

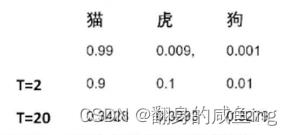
当我像更多的保留软标签也就是不同类别的概率值时可以通过T温度来改变。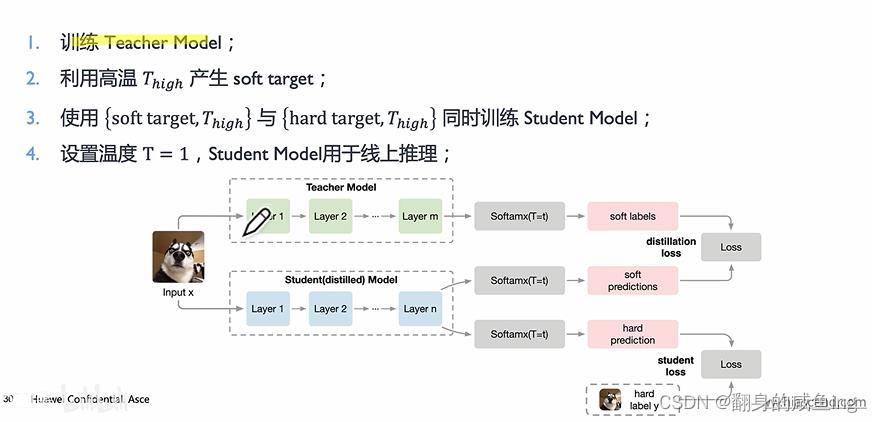 对于怎么训练学生模型,首先训练Teacher模型得到软标签
对于怎么训练学生模型,首先训练Teacher模型得到软标签

EWC算法的改进
在EWC(弹性权重共享)中,为了简化计算和降低计算成本,通常会假设费舍尔信息矩阵(Fisher Information Matrix,FIM)是一个对角矩阵。这意味着我们只考虑各个参数对应的费舍尔信息值,而忽略了参数之间的相互作用。
实际上,费舍尔信息矩阵是一个对称矩阵,其非对角元素表示不同参数之间的相关性。然而,在实际应用中,为了降低计算复杂性,通常会采用对角化近似。这种近似虽然可能损失了一些参数之间的相关信息,但在很多情况下,仍能取得较好的性能。
所以,在EWC中使用的费舍尔信息矩阵通常被近似为对角矩阵。这有助于简化计算,并在降低计算成本的同时仍能有效地保护先前任务的知识。
分类器的在线/增量学习
【中文标题】分类器的在线/增量学习【英文标题】:online/incremental learning for classifiers 【发布时间】:2015-03-07 20:50:49 【问题描述】:我了解,在在线/增量学习中,SVM 或 NN 可能会增量学习,因为新数据会随着时间的推移变得可用。如果随着时间的推移,现有案例的新功能/变量变得可用,而不是新案例,该怎么办。是否有任何技术可以处理这种分类器/预测的训练?
【问题讨论】:
【参考方案1】:对于神经网络,我会采用这种方法:
以已经训练好的网络为例。为新特征添加新的输入神经元。可选地将新神经元添加到隐藏层。用零或随机值初始化新连接的权重。重新训练网络。
它应该比从头开始训练一个新网络要快。
【讨论】:
以上是关于增量学习Contiual learning的主要内容,如果未能解决你的问题,请参考以下文章