二叉树刷题专练

Posted 2023-04-07 Ruiren_

文章目录

• 前言
• 一、二叉树的最小深度
• • 1.题目介绍
  • 2.思路
  • 3.代码
• 二、完全二叉树的节点个数
• • 1.题目介绍
  • 2.思路
  • 3.代码

---

前言

---

继承前面的写作思路，此篇文章继续二叉树的oj题

一、二叉树的最小深度

1.题目介绍

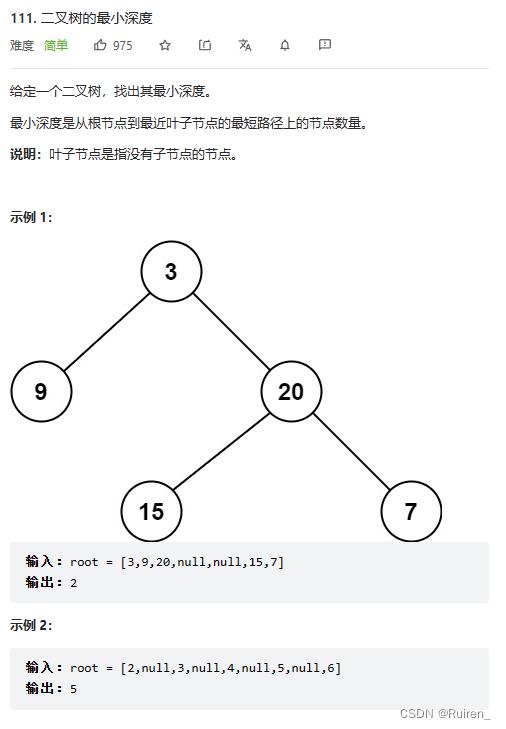
题目在力扣 二叉树的最小深度

2.思路

最小深度是从根节点到最近叶子节点的最短路径上的节点数量，叶子节点是没有子节点的节点，那么叶子节点的是不是只可能出现在一个字数遍历完才会出现，所以这题我们就可以转化成一个遍历到叶子的最短路径，那么们就会出现下面这种情况，这种情况数出5，即返回右子树的最小深度

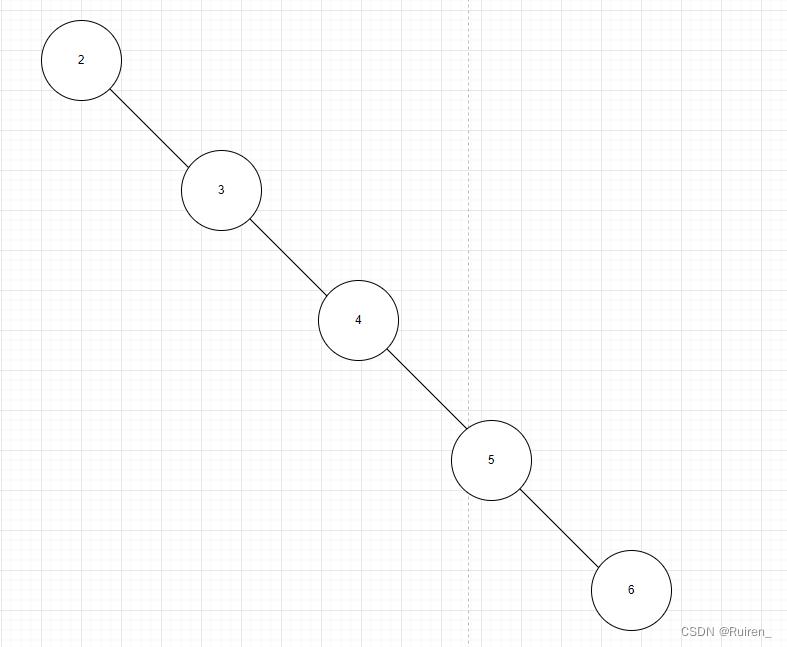
所以我们可以总结成以下几点

1.如果root为空，则返回0；
2.如果左节点为空，那么直接返回右节点的最小深度+1即可
3.如果左节点为空，那么直接返回右节点的最小深度+1即可
4.如果两者都不为空，我们就返回左节点和右节点中小的那个节点+1

3.代码

/**
 * Definition for a binary tree node.
 * struct TreeNode 
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * ;
 */
int minDepth(struct TreeNode* root)
    if(root==NULL)
    return 0;
    if(root->left==NULL)
    return minDepth(root->right)+1;
    else if(root->right==NULL)
    return minDepth(root->left)+1;
    int left=minDepth(root->left);
    int right=minDepth(root->right);
    if(left<right)
    
        return left+1;
    
    else
    
        return right+1;
    

二、完全二叉树的节点个数

1.题目介绍

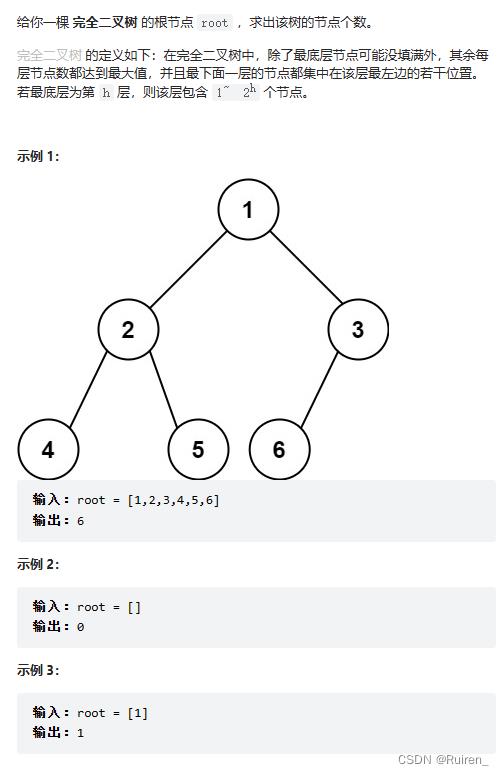
题目在力扣完全二叉树的节点个数

2.思路

本题考的就是层序遍历，将这课二叉树层序遍历一遍就行了，层序就是建立一个队列，利用队列的先进先出的性质，每pop一个节点，就依次带入其非NULL节点的左节点和右节点，如下图

你可以用数组模拟队列，也可以直接拿队列的代码来弄

3.代码

/**
 * Definition for a binary tree node.
 * struct TreeNode 
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * ;
 */
typedef struct TreeNode* QDatatype;
typedef struct QueueNode

	struct QueueNode* next;
	QDatatype Data;
QNode;

typedef struct Queue

	QNode* head;
	QNode* tail;
	int size;
Queue;

void QueueInit(Queue* pq)

    assert(pq);
    pq->head = pq->tail = NULL;
    pq->size = 0;


void QueueDestroy(Queue* pq)

    assert(pq);
    QNode* cur = pq->head;
    while (cur)
    
        QNode* next = cur->next;
        free(cur);
        cur = next;
    
    pq->head = pq->tail = NULL;
    pq->size = 0;



void QueuePush(Queue* pq, QDatatype x)

    assert(pq);
    QNode* newnode = (QNode*)malloc(sizeof(QNode));
    assert(newnode);
    newnode->Data = x;
    newnode->next=NULL;
    if (pq->size == 0)
    
        pq->head =pq->tail= newnode;
    
    else
    
        pq->tail->next = newnode;
        pq->tail = newnode;
    
    pq->size++;



void QueuePop(Queue* pq)

    assert(pq);
    assert(pq->size);
    if (pq->head->next==NULL)
    
        free(pq->head);
        pq->head =pq->tail= NULL;
    
    else
    
        QNode* next = pq->head->next;
        free(pq->head);
        pq->head = next;
    
    pq->size--;


int QueueSize(Queue* pq)

    assert(pq);
    return pq->size;


bool QueueEmpty(Queue* pq)

    assert(pq);
    return pq->size==0;


QDatatype QueueFront(Queue* pq)

    assert(pq);
    assert(!QueueEmpty(pq));
    return pq->head->Data;


QDatatype QueueBack(Queue* pq)

    assert(pq);
    assert(!QueueEmpty(pq));
    return pq->tail->Data;





int countNodes(struct TreeNode* root)
    if(root==NULL)
    return 0;
	Queue tree;
	Queue* pt = &tree;
	QueueInit(pt);
	QueuePush(pt,root);
    int count=0;
	while (!QueueEmpty(pt))
	
		struct TreeNode* front = QueueFront(pt);
        count ++;
		QueuePop(pt);
		if (front->left)
		
			QueuePush(pt, front->left);
		
		if (front->right)
		
			QueuePush(pt, front->right);
		
	
	QueueDestroy(pt);
    return count;

二叉树刷题

• 本文不是什么教程，没有案例说明，只是我用来记录刷题过程中的一些体会。
• 本文是按照公众号代码随想录提供的PDF进行学习，十分不错，给大家安利一波

二叉树刷题

二叉树的前中后遍历

• 二叉树的前中后遍历可以使用递归方法和迭代法进行遍历
• 在递归中，最大的体会就是程序由于递归的作用不断的向下执行，通过压栈把当前同级的后续操作进行保存，等到未来进行出栈进行操作。并且对于每个节点的操作都是在本次的递归中实现。
• 在迭代思想中，给我的感觉仍然是通过栈模拟了递归的过程，通过判断栈是否为空，让程序一直执行下去。通过压栈当前同级的后续操作进行保存，但是通过出栈处理不仅是执行之前压入的后续的同级操作，并且出栈的时候也要进行处理当前的节点。
• 递归和迭代的关系十分密切，但是不能直接照搬。至于为什么处理节点的时间点不一致，是因为遍历这个节点的时间不一样。在递归中，进入某次递归即视为遍历到该节点。在迭代中，出栈时候，视为遍历到该节点。也就是什么时候遍历到该节点，什么时候进行操作
• 在迭代的方式遍历时候，尤其是注意中序遍历，中序遍历的顺序是左中右，并且对节点的操作必须绑定在访问中间的那个节点时候，但是二叉树的访问必定是先中间节点开始，然后往下遍历。这个时候就要想办法，在访问中间节点时候，不视为遍历到该节点，当访问完左节点之后，在访问中间节点时候才视为遍历到该节点。综上，我们要借助额外的方法，使我们遍历的开始，就找到左边的节点。有一个办法就是使用一个指针，利用这个工具指针找到左节点。

二叉树的层序遍历

• 层次遍历借助的数据结构就是队列，在解题时候常常需要记录某一层的元素，这个时候可以使用双指针法，也可以使用当前的size作为标记

反转二叉树

• 由于树的结构特性，无非也是遍历的过程，在遍历的过程中对节点进行反转。在选取遍历过程中可以使用前后，层序遍历。并且基于结构特性，可以使用递归法，也可以使用迭代方法。
• 基于递归，以及节点访问的顺序，可以写出最容易想到的递归+先序遍历
• 迭代法的写法也是十分方便的，只不过是对每个节点的处理内容不一样，对节点处理的时间都和原来一模一样。

镜像二叉树

• 判断二叉树对称的关键并不是左右节点对等，而是左右子树互成镜像。这个时候思路要转变到，这不是在遍历一棵树，而是遍历两棵树，在遍历的过程中进行比较。并且是采用回溯的后续遍历。并且很容易就想到递归方式解决问题
• 对于为什么采用后续遍历的原因在于，在遍历A树的节点1时候，也要遍历B树的节点1，除了要判断这2个符合镜像之外，还需要判断对应的子树，所以两个节点是否镜像由三部分组成。必须等到子树判断之后才可以判断出结果，故要采用后续遍历。
• 同时也可以采用迭代的方式进行判断其实是把左右两个⼦树要⽐较的元素顺序放进⼀个容器，然后成对成对的取出来进⾏⽐较。

二叉树的最大深度

• 求二叉树的最大深度，也是从节点一直往下探索，所以每一个结点的深度是子树的深度加1。也就是判断一个节点的深度，需要利用到子树，这和镜像二叉树十分类似。所以这种情况下，遍历顺序选取后续遍历。
• 在迭代版本的算法中，可以使用层次遍历的遍历顺序方式。

二叉树的节点个数

• 和前面的思路十分相似，处理左右节点之后加上本节点，采用后续遍历的方法
• 当然采用迭代方式，也是可以的

二叉树的高度

• 二叉树的高度采用后续遍历，二叉树的深度采用先序遍历，而二叉树的最大深度和最大高度是一样的，所以在求最大的时候两个遍历顺序都可以
• 但是为了逻辑上的一致性，尽量配套使用
• 但是求高度的时候，不能用层次遍历。不过可以使用一个函数，把传入的节点当作根节点，利用求其根节点的最大高度就是最大深度，求的最大高度。

二叉树的全部路径

• 在递归方式的回溯中，一定要注意什么时候回溯，其实回溯就是利用了递归的特性，就是递归返回时候，会执行过去未执行的，暂存的同级操作。

左叶子之和

• 这道题其实也是很常规，求左叶子之和，要判断是叶子，是左叶子，所以利用父节点进行判断。这个时候也可以把左叶子之和记录在父节点身上，也是就是我们计算左叶子之和，就是计算某个节点的左右子树中的左节点之和。故，熟悉的套路又来咯，在递归方式中先搞左右，在搞中间，所以采用后序遍历。
• 在迭代版本中，出栈的节点可以判断是否含有左叶子，所以在迭代的版中可以采用先中后都可以。我个人是觉得在迭代方式中使用先序是最符合逻辑的。

寻找最左边的值

• 如果需要遍历整颗树，递归函数就不能有返回值。如果需要遍历某⼀条固定路线，递归函数就⼀定要有返回值！
• 当然使用层次遍历岂不美哉

路径之和

• 112题和113题，确实不错

构造二叉树

• 掌握好理论构造方便，注意边界问题就可以

合并二叉树

• 这道题的关键是同时遍历两颗二叉树，这和之前判断二叉树是否镜像是一模一样的套路
• 使用递归方法就按照常规分析就可以，使用迭代方式，可以使用层序遍历。利用一个队列数据结构就可以。

二叉树中的搜索

• 二叉树如果是二叉搜索树的话，不用回溯