Leetcode-不同路径I和II（计数型动态规划）

Posted 2023-02-18 Booksort

目录

62.不同路径

第一步：确定状态

最后一步

子问题

第二步：确定初始状态和边界

第三步：计算顺序

代码实现

63.不同路径II 

特殊情况分析

代码实现

---

62.不同路径

62.不同路径

 

 本题使用动态规划来解决，符合计数型动态规划的情况。

第一步：确定状态

通过最后一步来推到子问题，可以得到问题之间的递归关系

最后一步

机器人到达(m,n)位置，只能通过(m-1,n)+1和(m,n-1)+1到达，且机器人到达(m-1,n)/(m,n-1)也算通过其点的两个点达到…，以此类推

假设m=1,n=1，那么从(0,0)到达(1,1)只有两种方法，到(1,0)，(0,1)，就是1+1

子问题

此问题情况满足加法原则：情况无重复、无遗漏。

针对此题而言，到(m-1,n)和(m,n-1)的路径的情况是不可能重复的，因为只允许向右向下移动。

如果机器人有X种路径到达(m-1,n-1)，Y种路径到达(m-2,n)，则机器人有X+Y种路径到达(m-1,n)

所以，求到(m,n)有多少种路径，变成了分别求到(m-1,n)、(m,n-1)分别有多少路径，这样可以减小棋盘的规模大小

状态：f(i,j)-从（0，0）到（i，j）有多少中不同的路径

二维问题，遍历二维数组

状态转移方程：加法原则-f(i,j)=f(i-1,j)+f(i,j-1)

第二步：确定初始状态和边界

从（0，0）开始，且棋盘是有边界的，下标要大于等于0，才能进入计算

向下和向右走一步，计数就加一

初始位置就是（0，0），从（0，0）到（0，0）就只有一种情况可以到达f(0,0)=1

对于i=0或者j=0的位置，需要判断，且值只有一个方向路径，当满足状态转移方程时，j<0/i<0的位置的值为0

第三步：计算顺序

从最基本的初始情况的子问题开始，对于二维的，可以向遍历二维数组一样，一行一行计算，也可以一列一列计算

时间复杂度O(N^2),空间复杂度O(N^2)

代码实现

class Solution 
public:
    int uniquePaths(int m, int n) 
        vector<vector<int>> arr;
        for(int i=0;i<m;i++)
        
            vector<int> v(n);
            arr.push_back(v);
        
        arr[0][0]=1;
        for(int i=0;i<m;i++)
        
            for(int j=0;j<n;j++)
            
                if(i==0&&j==0)
                
                    continue;
                
                arr[i][j]=0;
                if(i-1>=0)
                
                    arr[i][j]+=arr[i-1][j];
                
                if(j-1>=0)
                
                    arr[i][j]+=arr[i][j-1];
                
            
        
        return arr[m-1][n-1];
        
    
;

63.不同路径II

63.不同路径II 

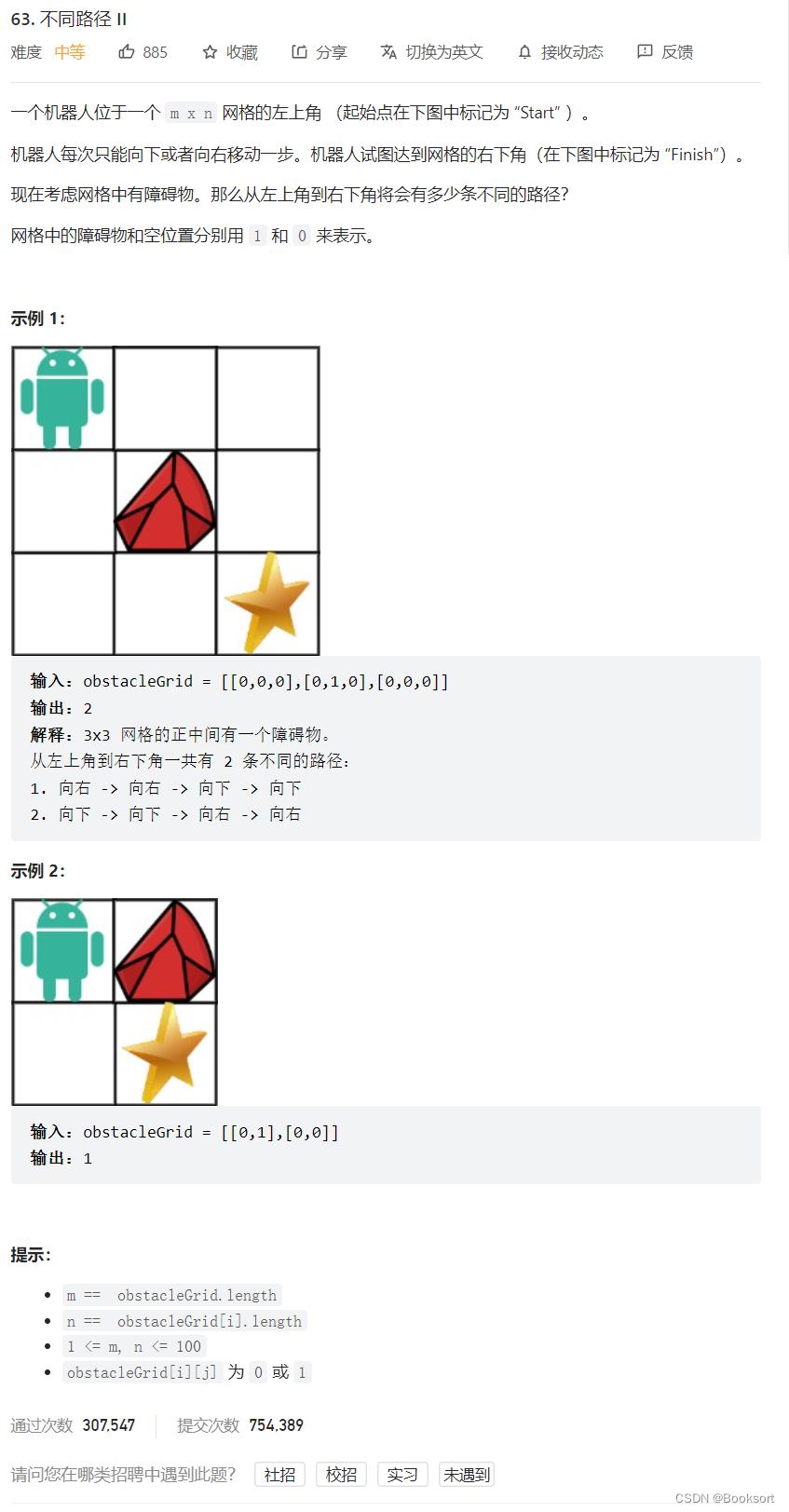
 本题具体分析是和62题分析的步骤逻辑、流程是几乎一样的。

特殊情况分析

但是有一点不同，就是出现了障碍物，这个需要单独去判断，同时还需要考虑一下边界条件的设置

对于边界条件，也就是i==0或者j==0的边界路径数，这个不能直接设置值为1，需要结合状态转移方程f(i,j)=f(i-1,j)+f(i.j-1)

对于障碍物的值的设置为0，同时还要判断。

否则会出现，0,0,0,1,1,0的情况。该测试得到的结果是0，唯一的路被障碍物挡住了无法到达目的地，所以才需要利用状态转移方程来计算边界值，同时还需要考虑起点和终点也是障碍物的情况，都是返回值为0.

代码实现

class Solution 
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) 
        int ROW=obstacleGrid.size();
        int COL=obstacleGrid[0].size();
        if(obstacleGrid[0][0]==1||obstacleGrid[ROW-1][COL-1]==1)
            return 0;
            
        
        vector<vector<int>> arr;
        for(int i=0;i<ROW;i++)
        
            vector<int> v(COL);
            arr.push_back(v);
        
        arr[0][0]=1;
        for(int i=0;i<ROW;i++)
        
            for(int j=0;j<COL;j++)
            
                if(i==0&&j==0)
                    continue;
                int m=0,n=0;
                if(obstacleGrid[i][j]==1)//障碍物不带入计算
                
                    m=0;
                    n=0;
                
                else if(i==0)//防止唯一路径被障碍物挡住
                
                    n=arr[i][j-1];
                
                else if(j==0)//防止唯一路径被障碍物挡住
                
                    m=arr[i-1][j];
                
                else
                
                    m=arr[i-1][j];
                    n=arr[i][j-1];
                
                arr[i][j]=m+n;
            
        
        return arr[ROW-1][COL-1];
    
;