广州大学第十七届ACM大学生程序设计竞赛（同步赛）

Posted 2023-04-06 WQhuanm

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了广州大学第十七届ACM大学生程序设计竞赛（同步赛）相关的知识，希望对你有一定的参考价值。

A-萤火虫

思路：

我们只用操作1，是不是能贪心都前面n-k个数都是0。
如果我们对于1<=i<=n，归为k个集合，即s[j]=s[i%k],我们每操作一次操作1，s[0]~s[k-1]都会一起加1或者减1，如果我们最后能减到都同时0，就说明成功了。
而我们可以贪心到最后只剩k个数，那么他们就对应各自的s[j]，我们可以对最后这k个数操作一次操作1，尽可能多的使这一次将更多数变为0，剩下不为0的显然只能使用操作2，即答案。

#include <bits/stdc++.h>
using namespace std;
#define ll     long long
const int N = 2e5 + 10;

ll a[N];
int main()

	int t;
	cin>>t;
	while (t--)
		
			int n,k,x;
			cin>>n>>k;
			fill(a,a+n+1,0);
			for (int i=0; i<n; ++i)
				
					cin>>x;
					a[i%k]+=x;//把数分为k个集合，每次操作1就等效对每个集合操作
				
			if (k==1)
				
					cout<<0<<endl;
					continue;
				
			sort(a,a+k);
			int len=0;
			int p=1;
			for (int i=1; i<k; ++i)
				
					if (a[i]==a[i-1])p++;
					else
						
							len=max(p,len),p=1;//最后一次操作1尽可能使多的集合变为0
						
				
			len=max(p,len);
			cout<<k-len<<endl;
		
	return 0;

B-罗伯特

思路：

显然用bfs去跑即可，为了使一个点不要重复经过，我们可以记录每个点在方向f时的最短路是多少，只更新更短的

#include <bits/stdc++.h>
using namespace std;
#define ll     long long
#define int ll
typedef pair<int, int> pii;
const int N = 110;

struct node

	int d,x,y,p,f;
	bool operator<(const node&k)const
	
		return d>k.d;
	
;
int dp[N][N][60][5];
bool vis[N][N][60][5];
int ways[5][3]= -1,0,1,0,0,-1,0,1;
pii mp[N][N];
char ch[N][N];
int32_t main()

	int n,m,p,k;
	cin>>n>>m>>k>>p;
	int x1,y1,x2,y2;
	for (int i=1; i<=k; ++i)
		
			cin>>x1>>y1>>x2>>y2;
			mp[x1][y1]= x2,y2;
			mp[x2][y2]= x1,y1;
		
	memset(dp,0x3f,sizeof(dp));
	for (int i=1; i<=n; ++i)for (int j=1; j<=m; ++j)
			
				cin>>ch[i][j];
				if (ch[i][j]=='U')ch[i][j]='0';
				else if (ch[i][j]=='D')ch[i][j]='1';
				else if (ch[i][j]=='L')ch[i][j]='2';
				else if (ch[i][j]=='R')ch[i][j]='3';
			
	priority_queue<node>q;
	dp[1][1][0][3]=0;
	q.push(0,1,1,0,3);
	while (!q.empty())
		
			node u=q.top();
			q.pop();
			if (vis[u.x][u.y][u.p][u.f])continue;
			vis[u.x][u.y][u.p][u.f]=1;
			if (u.x==n&&u.y==m)
				
					cout<<"YES"<<endl;
					cout<<dp[u.x][u.y][u.p][u.f]<<endl;
					return 0;
				
			if (ch[u.x][u.y]=='.')
				
					for (int i=0; i<4; ++i)
						
							node v=u;
							v.x+=ways[i][0],v.y+=ways[i][1],v.p+=(i!=v.f);
							v.f=i;
							if (1<=v.x&&v.x<=n&&1<=v.y&&v.y<=m&&ch[v.x][v.y]!='#')
								
									if (mp[v.x][v.y].first!=0)
										
											pii tmp=mp[v.x][v.y];
											v.x=tmp.first,v.y=tmp.second;
										
									if (v.p<=p&&dp[v.x][v.y][v.p][v.f]>dp[u.x][u.y][u.p][u.f]+1)
										
											dp[v.x][v.y][v.p][v.f]=v.d=dp[u.x][u.y][u.p][u.f]+1;
											q.push(v);
										
								
						
				
			else if (('0'<=ch[u.x][u.y]&&ch[u.x][u.y]<='3')||ch[u.x][u.y]=='@')
				
					node v=u;
					if (ch[u.x][u.y]!='@')v.f=ch[u.x][u.y]-'0';
					v.x+=ways[v.f][0],v.y+=ways[v.f][1];
					if (1<=v.x&&v.x<=n&&1<=v.y&&v.y<=m&&ch[v.x][v.y]!='#')
						
							if (mp[v.x][v.y].first!=0)
								
									pii tmp=mp[v.x][v.y];
									v.x=tmp.first,v.y=tmp.second;
								
							if (v.p<=p&&dp[v.x][v.y][v.p][v.f]>dp[u.x][u.y][u.p][u.f]+1)
								
									dp[v.x][v.y][v.p][v.f]=v.d=dp[u.x][u.y][u.p][u.f]+1;
									q.push(v);
								
						
				
		
	cout<<"NO"<<endl;
	return 0;

C-论AE自动化的重要性

思路：

裸拓扑，反向建边即可

#include <bits/stdc++.h>
using namespace std;
#define ll     long long
#define int ll
const int N = 2e5 + 10;
const int mod=1e9+7;

ll a[N],in[N];
struct node

	int next,to,w;
 edge[N<<1];
int head[N],num;

void add(int u,int v,ll w)

	edge[++num].next=head[u];
	edge[num].to=v,edge[num].w=w;
	head[u]=num;


int32_t main()

	int n,m,k;
	cin>>n>>m>>k;
	int x,y,c;
	for (int i=1; i<=k; ++i)
		
			cin>>x>>y;
			a[x]+=y;
		
	for (int i=1; i<=m; ++i)cin>>x>>y>>c,add(y,x,c),in[x]++;
	queue<int>q;
	ll ans=0;
	for (int i=1; i<=n; ++i)if (!in[i])q.push(i);
	while (!q.empty())
		
			int u=q.front();
			q.pop();
			ans=(ans+a[u])%mod;
			for (int i=head[u]; i; i=edge[i].next)
				
					int v=edge[i].to,w=edge[i].w;
					a[v]=(a[v]+a[u]*w)%mod;
					if (--in[v]==0)q.push(v);
				
		
	cout<<ans<<endl;
	return 0;

G-Clannad

思路：

目标是取n+1个不相同的数，使得这些数存在有两个数差是n倍数。因为n+1>n，所以如果这n个数mod n。必然有两个余数相同，那么他们的差绝对值就是n了
所以问题转化为如果x>=n+1(使得可以取n+1个不同的数），那就是组合数，在x个数选n+1个数。所以预处理组合数即可

#include <bits/stdc++.h>
using namespace std;
#define ll     long long
#define endl             "\\n"
const int N = 5e3 + 10;
const int mod=1e9+7;

ll c[N][N];
void init()

	c[0][0]=1;
	for (int i=1; i<=5e3; ++i)
		
			c[i][0]=1;
			for (int j=1; j<=i; ++j)c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
		


int main()

	std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int t,n,x;
	cin>>t;
	init();
	while (t--)
		
			cin>>n>>x;
			if (n+1>x)
				
					cout<<-1<<endl;
					continue;
				
			else
				
					cout<<c[x][n+1]<<endl;
				
		
	return 0;

H-性格差劲的久美子

思路：

首先如果a的数字b里面没有，显然这个数字排在哪里都可以。
而对应x,y同时属于a与b数组，那么我们假设x在b中出现范围是L[x]~R[x],y范围是L[y]~R[y]，那么我们需要满足x,y在a的子串出现范围是R[y]<=L[x]
所以我们可以先处理b中每个数在b的出现范围
然后顺序遍历a。设t[i]表示在i位置之后出现了多少个位置
1. 如果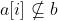,那么显然答案子串可以直接无视顺序加它。
2. 如果属于，那么a[i]可以匹配b中所有在a[i]最后一次出现后的数字+1（t记录的数字都是在a数组中在a[i]出现前的，我们这样加（表示他们都是在b中顺序是在a之后出现的）。然后再对a[i]第一次出现及其之前的位置更新t[i],表示这些区间可以出现a[i]
因为维护区间数个数，每次都是单点修改，所以树状数组功能足够了

#include <bits/stdc++.h>
using namespace std;
#define ll     long long
#define endl             "\\n"
typedef pair<int, int> pii;
const int N = 2e5 + 10;
int t[N],a[N],b[N];
unordered_map<int,pii>mp;
void add(int x,int w)

	for (int i=x; i; i-=i&-i)t[i]=max(t[i],w);

int ask(int x)

	int ans=0;
	for (int i=x; i<=N; i+=i&-i)ans=max(ans,t[i]);
	return ans;


int main()

	int n,m;
	cin>>n;
	for (int i=1; i<=n; ++i)cin>>a[i];
	cin>>m;
	for (int i=1; i<=m; ++i)
		
			cin>>b[i];
			if (!mp[b[i]].first)mp[b[i]]= i,i;//更新每个在b中出现的数的出现区间
			else mp[b[i]].second=i;
		
	int ans=0,sum=0;
	for (int i=1; i<=n; ++i)
		
			if (!mp[a[i]].first)sum++;//b中没出现直接加
			else
				
					int tmp=ask(mp[a[i]].second)+1;//找符合条件的最长子串，寻找在b数组顺序在a[i]之后出现的数（这些数在a数组中是在a之前出现，先出现才能被加到t数组里面）
					ans=max(ans,tmp);
					add(mp[a[i]].first,tmp);//更新t数组中出现的数字的区间
				
		
	cout<<ans+sum<<endl;
	return 0;

K-因子模仿

思路：

注意到[l,r]胜利与否结果就是r是1还是0，所以我们在区间操作中维护每个数被修改次数即可，奇数次转变奇偶性，偶数次等价没修改。所以其实是树状数组裸题

#include <bits/stdc++.h>
using namespace std;
#define ll     long long
#define endl             "\\n"
const int N = 1e6 + 10;
int t[N];
int n,q,x,op,l,r;
void add(int x,int w)

	for (int i=x; i<=n; i+=i&-i)t[i]+=w;

int ask(int x)

	int ans=0;
	for (int i=x; i; i-=i&-i)ans+=t[i];
	return ans;

int main()

	std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin>>n>>q>>x>>x>>x>>x;
	char c;
	for (int i=1; i<=n; ++i)
		
			cin>>c;
			if (c=='1')add(i,1),add(i+1,-1);
		
	while (q--)
		
			cin>>op>>l>>r;
			if (op==1)
				
					add(l,1),add(r+1,-1);//区间修改
				
			else
				
					if (ask(r)&1)//单点查询
						
							cout<<"Magical Splash Flare"<<endl;
						
					else
						
							cout<<"HoloPsychon"<<endl;
						
				
		
	return 0;

第十七届全国大学生智能车竞赛分赛区比赛线上赛流程规范（草案）

(正式稿件在竞赛网站公布) smartcar.cdstm.cn

§01 线上比赛流程

1.1 背景介绍

在2022年暑期举办的 第十七届全国大学生智能车竞赛 将会在 七、八两个月内分别在八个分（省）赛区 举行。根据 6月初召开的暑期比赛准备会议 上的讨论，为了适应防疫要求，部分分（省）赛区（东北、华北、西部、安徽、山东）将会采用线上比赛的形式。根据往年 线上比赛流程规范 以及今年部分省赛线上比赛的经验，制定第十七届全国大学生智能车竞赛线上比赛规范，用于指导线上比赛分赛区、省赛区组织比赛。

1.1.1 线上竞赛优点

在最大满足今年防疫要求的基础上，采用线上比赛的形式，可以：

节省参赛队伍旅行和住宿的费用；
可以更加充分完成赛场的适应和准备；也可以允许每支队伍参加多场的比赛；、
通过云端直播，加大了相互观摩和交流的机会，并提高竞赛的公平、公开、公正；

1.1.2 线上竞赛需避免问题

采用线上比赛，需要关注并采取措施避免可能出现的竞赛问题，包括：

提高比赛结果的可比性；尽量规范比赛赛道标准，采用多次比赛平均的方法，避免比赛结果与环境、地点、时间相关联性；
提高比赛公平、公正、公开，避免局部弄虚作假；要求多个学校组成线上比赛赛点进行比赛；
设计比赛赛道，尽量能够满足各个参赛队伍搭建的需求，避免参赛学校在时间、经费、人力等方面的费用；
在举行云比赛之前，需要对所有担任云比赛裁判进行培训、认证，避免现场裁判不标准造成评分混乱。
在每场比赛之前进行裁判和参赛队伍流程演练，所有参赛队伍尽可能在统一天举行比赛；
建议现场裁判与远程裁判共同给出成绩有效认证确认，车模检查确认，避免比赛内卷。

1.1.3 线上比赛原则

组委会远程视频监督：竞赛组委会通过腾讯会议（或者其他网络会议平台）对线上比赛进行全程监督；
视频直播公开：通过视频公开直播比赛过程，可以体现比赛的公平、公正、公开，鼓励参赛同学观摩交流，提高竞赛观赏性和影响力。比赛现场的搭建、队伍对比赛场地适应调试不在视频公开直播强制要求之内。
流程标准化：分散在不同时间、不同地点的线上比赛，为了提高比赛公平性、比赛成绩可比性、比赛过程严谨，需要对比赛流程制定标准化流程。包括：
（1）比赛内容标准（比赛环境、赛道、比赛任务）
（2）比赛组织标准（现场比赛组织、裁判、仲裁）
（3）比赛流程标准（车模技术检查与公示、比赛顺序和时间安排）。
（4）比赛信息标准（参赛队伍信息认证、比赛现场视频场景、比赛计时、车模技术文档）。
多所学校组合：通过多所学校（2~10所学校）组合形成线上比赛赛点，可以有以下优点：
（1）在满足常态化防疫要求情况下，可以增加比赛队伍之间相关观摩和交流；
（2）对于比赛环境所需要的竞赛物资（赛道、比赛系统等、环境布置）费用可以相互均摊；
（3）可以有足够人员来组成比赛标准化流程所需要的比赛人员（组织人员、裁判员、仲裁人员等）；
（4）各学校可以相互监督，共同维护比赛公平。
专家入校比赛：对于条件允许的赛区，也可以采用组委会专家入校完成比赛的方式。

1.2 赛前工作

1.2.1 分赛区组委会

（1）公布比赛群和联系方式

在6月底，分赛区组委会完成以下工作：

公布通过竞赛网站公布分赛区比赛带队教师和学生交流群，用于和参赛队伍带队教师和参赛学生交流沟通，发布比赛实时信息等；
公布接收参赛信息邮箱和联系人信息，用于接收参赛队伍报名信息、车模技术报告、比赛过程记录信息等；
从竞赛网站下载报名队伍信息，并通过电话逐一确认参赛信息；公布参赛队伍统计信息；可以要求所有参赛队伍将最终的队伍参赛信息（包括学校队伍名称、参赛组别、学生和指导教师信息等）在比赛前两周时间通过电子邮件发送到组委会；
公布线上比赛流程：包括线上比赛开幕式安排（根据需要设置开幕式环节）、线上比赛演练时间、线上正式比赛时间以及结果公示时间等。

（2）公布线上赛点信息

接收参赛队伍提交的参赛信息，包括参赛车模就初始检查信息、赛道高校组合信息等。详细要求，参见后面队伍提交信息中的内容。在比赛前一周的时间，根据参赛队伍提交的比赛信息，公布比赛各个赛点信息，其中包括包括：

赛点学校与队伍信息；赛道竞赛组织者信息等；
赛道环境信息和比赛时间流程信息；
比赛公开B站网络直播信息；

（3）赛前检查演练

在正式比赛之前，与每个赛点进行比赛演练。竞赛组委会通过腾讯会议与参赛队伍进行远程演练：

对赛点比赛流程、比赛环境、比赛赛道、裁判系统进行检查，要求符合比赛规范。具体要求参见《第十七届全国大学生智能车裁判员手册》；
确定比赛流程，包括比赛组别顺序、成绩认证过程、车模检查过程以及参赛队伍数据提交过程；
确定比赛现场B站直播条件、直播网络信息等；
参赛队伍对比赛过程进行熟悉，保证正式比赛进展顺利。

1.2.2 参赛学校和队伍

（1）与分赛区组委会联系

参加暑期分赛区智能车竞赛的队伍，在6月底之前在竞赛网站完成报名。并根据分赛区组委会公布的比赛群和联系方式完成：

指导教师与参赛领队分别进入各分赛区比赛联系群；
确认分赛区组委会发布的报名统计信息是否包含有参赛队伍的正确信息：包括学校队伍名称、参赛队员与指导教师信息、参赛组别信息等。在比赛之后这些信息都不允许进行修改；
根据分赛区要求，参赛队伍将报名的最终信息发送到组委会。

（2）完成赛点组合

根据线上比赛原则，参加竞赛的队伍根据所处赛区组委会要求，可以采用线上远程比赛模式、专家入校比赛模式两种之一。

对于采用专家入校比赛模式赛区，每个学校的参赛队伍可以自行确定比赛的地点，并在规定时间，在专家裁判在现场的情况下完成比赛，并确认竞赛成绩。比赛过程要求进行现场直播。

对于采用远程线上比赛模式的赛区，要求参赛学校队伍组成赛点完成线上比赛。这个过程分为三个阶段：

阶段1：赛点组合阶段
在采用线上比赛的赛区内，原则上参赛队伍以学校为单位，在同一赛区内，2~10所高校组成高校竞赛组合，在同一时间、同一地点组织比赛。组合在一起的队伍信息，按照统一要求在比赛前一周向分赛区组委会提交参赛队员、比赛组织人员、比赛直播流程等详细信息表格。
阶段2：比赛演练阶段
赛点组合根据分赛区组委会要求，在正式比赛时间之前进行完成比赛演练。组委会对赛点比赛场地、裁判系统、比赛流程进行确认，对于需要修改的问题进行调整。通过演练过程，参赛队员以及组委会裁判按照裁判员手册能够完成对比赛成绩的确认。
阶段3：线上比赛阶段
赛点在比赛时间段，根据统一比赛流程完成线上比赛并完成成绩确认。同期进行网络直播。

由于客观原因，无法组成多个高校赛点的参赛队伍，可以单独与分赛区组委会进行联系，确认参赛方式。原则上单独完成比赛的队伍不能进入全国总决赛。

（3）提交参赛队伍信息

参加竞赛的队伍，在比赛前一周，分赛区组委会提交以下信息：

赛点高校信息：每个赛点高校，统一向竞赛组委会提交一份《线上竞赛高线组合信息表格》，可以在7月5日之后在竞赛网站下载。
赛道比赛信息 ：包括有：
- 高校组合赛点比赛流程简介：包括比赛时间安排、比赛场地铺设规格、裁判系统、车模技术检查流程安排等；
- 比赛场地展示：通过图片，或者视频对于比赛铺设场地，环境进行展示；
- 比赛直播网站链接：比赛直播网站链接信息，建议通过B站进行比赛过程直播，也可以采用其他成熟稳定的视频直播平台；
车模技术报告 ：这是用于车模技术检查的技术报告，具体要求参见竞赛网站公布的参赛车模技术报告要求。每一支队伍根据最终参赛车模技术状态，单独形成一份技术报告提交给组委会。

1.3 比赛过程

在比赛当天，赛点按照确定的比赛时间以及前面演练的比赛流程进行比赛。下面给出比赛的主要关键环节。

1.3.1 比赛场地与流程确认

在比赛正式之前，竞赛组委会将会通过远程腾讯会议与赛点负责人对于比赛场地、计时方法、比赛流程以及车模检查方法进行确认。在比赛技术细节确认之后，赛点便可以进行正式比赛。

赛点可以根据参赛学校和队伍情况以及比赛流程安排确定是否举行简短的比赛开幕式、比赛的闭幕式。

1.3.2 正式比赛

按照赛道的比赛流程，按照一定组别顺序每个参赛队伍逐一进行比赛。

每个组别比赛的流程和成绩确定请参照《第十七届全国大学智能车竞赛裁判员手册》。现场比赛组办方和远程组委会承办人员需要详细了解智能车竞赛比赛规则以及裁判员手册内容。

1.3.3 比赛流程直播与解说

对于每一个组别比赛过程需要进行现场直播。要求有一名老师或者同学对于比赛流程进行解说，内容包括：

播报现在进行比赛的队伍信息，以及进入比赛现场之前车模初步检查情况；
播报每一次比赛比赛成绩以及相应的判罚标准；
播报比赛队伍比赛次数和现场比赛时间等；
对于现场出现的意外情况进行介绍；

每一个队伍在完成之后，需要在纸质的成绩确认单上进行签字。

成绩确认单可以由各赛点自行设计格式。最后的成绩确认当需要有赛点仲裁组负责人签字后，按照下面赛后工作要求提交给竞赛组委会。

1.3.4 车模技术检查

对于车模进行技术检查，可以安排在比赛之前，也可以安排在比赛之后。

各赛点对于车模技术检查可以采用如下两种模式：

集中检查模式：也就是在比赛完成之后，统一对于参赛车模进行集中技术检查。这要求每个队伍的车模在比赛完成之后，需要立即放置在统一的车模展示区，由现场技术组负责人组织老师和同学共同进行技术检查；
随赛即检模式：每个车模在完成成绩确认之后，立即到现场技术组进行技术车模检查；

技术组在完成车模检查之后出具一份车模检查汇总信息。对于每一支参赛队伍车模检查是否与他们提供的车模技术检查表相符进行判断，并对车模是否满足比赛组别技术要求作出总结，对于出现的特异情况进行说明。

对于车模检查过程可以通过B站直播，或者腾讯会议展示给竞赛组委会。

1.4 赛后工作

1.4.1 提交比赛资料

在完成线上比赛之后，高校组合赛点在比赛当天向竞赛组委会提供如下资料：

1. 现场全体队员合影；如果队员很多，也可以分组拍摄发送过来。合影可以在赛前拍摄，也可以在赛后拍摄；
2. 比赛工作人员合影；包括赛点各组别负责人、现场裁判人员等；
3. 队员签字以及裁判签字确认的成绩表格照片；车模检查表汇总信息；
4. 录有比赛成绩的比赛成绩表格（可以直接在高校组合信息excel 文件中队伍信息表格中最后一栏给出）；
5. 车模检查表电子文档。可以在竞赛网站下载第十七届全国大学生智能汽车竞赛车模技术检查表格与技术文件文件，每个队伍按照文件要求提交车模车模技术检查表格与技术文件；
6. 比赛直播录像下载地址。这个信息不必在比赛结束当天提供。