2021SC@SDUSC-SEAL全同态加密库
Posted Be a good thinker
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2021SC@SDUSC-SEAL全同态加密库相关的知识,希望对你有一定的参考价值。
SEAL全同态加密库(四)
一.加密Encrypt
首先是两个构造函数,分别是解密的两种带入方式
public Encryptor(SEALContext context, PublicKey publicKey, SecretKey secretKey = null)
if (null == context)
throw new ArgumentNullException(nameof(context));
if (!context.ParametersSet)
throw new ArgumentException("Encryption parameters are not set correctly");
if (!ValCheck.IsValidFor(publicKey, context))
throw new ArgumentException("Public key is not valid for encryption parameters");
if (null == secretKey)
NativeMethods.Encryptor_Create(
context.NativePtr, publicKey.NativePtr, IntPtr.Zero, out IntPtr ptr);
NativePtr = ptr;
else
if (!ValCheck.IsValidFor(secretKey, context))
throw new ArgumentException("Secret key is not valid for encryption parameters");
NativeMethods.Encryptor_Create(
context.NativePtr, publicKey.NativePtr, secretKey.NativePtr, out IntPtr ptr);
NativePtr = ptr;
public Encryptor(SEALContext context, SecretKey secretKey)
if (null == context)
throw new ArgumentNullException(nameof(context));
if (!context.ParametersSet)
throw new ArgumentException("Encryption parameters are not set correctly");
if (!ValCheck.IsValidFor(secretKey, context))
throw new ArgumentException("Secret key is not valid for encryption parameters");
NativeMethods.Encryptor_Create(context.NativePtr, IntPtr.Zero, secretKey.NativePtr, out IntPtr ptr);
NativePtr = ptr;
以下是解密的方法
public void Encrypt(
Plaintext plain, Ciphertext destination,
MemoryPoolHandle pool = null)
if (null == plain)
throw new ArgumentNullException(nameof(plain));
if (null == destination)
throw new ArgumentNullException(nameof(destination));
IntPtr poolHandle = pool?.NativePtr ?? IntPtr.Zero;
NativeMethods.Encryptor_Encrypt(
NativePtr, plain.NativePtr, destination.NativePtr, poolHandle);
public void EncryptZero(
ParmsId parmsId, Ciphertext destination,
MemoryPoolHandle pool = null)
if (null == parmsId)
throw new ArgumentNullException(nameof(parmsId));
if (null == destination)
throw new ArgumentNullException(nameof(destination));
IntPtr poolHandle = pool?.NativePtr ?? IntPtr.Zero;
NativeMethods.Encryptor_EncryptZero1(
NativePtr, parmsId.Block, destination.NativePtr, poolHandle);
public void EncryptZero(Ciphertext destination, MemoryPoolHandle pool = null)
if (null == destination)
throw new ArgumentNullException(nameof(destination));
IntPtr poolHandle = pool?.NativePtr ?? IntPtr.Zero;
NativeMethods.Encryptor_EncryptZero2(NativePtr, destination.NativePtr, poolHandle);
二.加密过程
加密过程看起来有点像公钥生成过程。
加密明文的过程是将一个系数模为t的多项式转换为一对系数模为q的多项式。本例中,我们将加密一个非常简单的多项式(称为消息) - m = 3 + 4x8 ≡ 3−3x8 – 只有两个不为零的系数。
加密还需要三个小的多项式。两个噪音多项式来自于相同的离散高斯分布(即和公钥中的噪音多项式的取法一样),另一个多项式我们称之为u,它的系数为-1、0或1,就像私钥一样。
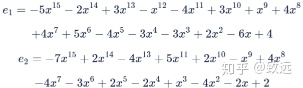
这些多项式只在加密过程中使用,然后丢弃。
密文是由两个多项式组成的,通过如下计算得到
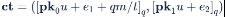
请注意消息中的值是在mod t的范围内,而在我们的示例中,它们被缩放为q/t (即128),使它们覆盖mod q的范围。这是消息被插入到密文时的唯一更改。这些值通过添加到第一项来掩盖,第一项的值是在mod q的范围内,与随机的噪音没有区别。u的随机性改变了每次加密中使用的掩码,从而确保相同的明文在每次加密时产生不同的密文。

同态加法和乘法之所以有效,是因为消息在密文中以比例来表示。其他项用于掩盖消息,而且可以证明它们是有效的,只有在您知道私钥的情况下才能删除它们。
使用上面给出的多项式显式地计算密文的第一个元素

代入公钥,我们可以看到密文的第一个元素展开为ct0 =[e1 + eu – aus + qm / t]q。在这个表达式中,前两项是“小”的,与噪音成比例,后两项是“大”的。第一个大项有效地掩盖了第二个大项,即消息。
密文的第二个元素是这样计算的:

代入公钥,我们看到密文的第二个元素展开为ct1 = [au + e2]q。这说明了解密是如何工作的——如果我们知道s,就可以计算出ct1s = [aus + e2s]q,它可以用来消除密文的第一个元素中的非消息大项。
综上所述,密文可以用公钥、私钥、掩码、噪音和消息表示为
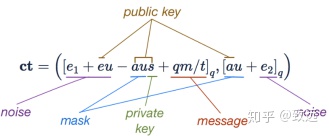
SEAL全同态加密开源库(十三) CKKS-源码浅析
2021SC@SDUSC
2021-12-26
前言
这是SEAL全同态加密开源库分析报告的第13篇,我们继续上一篇的CKKS源码分析。
代码分析
现在x3_encryption与x1_encryption处于不同的级别,这阻止我们将它们相乘来计算x3。
我们可以简单地将x1_encrypted切换到模数转换链中的下一个参数。然而,由于我们仍然需要将x3,乘以PI(plain_coeff3),所以我们先计算PI*x,然后将它与x2相乘,得到PI *x3。最后,我们计算PI *x 并将其从280缩放到接近2^40的值。
print_line(__LINE__);
cout << "Compute and rescale PI*x." << endl;
Ciphertext x1_encrypted_coeff3;
evaluator.multiply_plain(x1_encrypted, plain_coeff3, x1_encrypted_coeff3);
cout << " + Scale of PI*x before rescale: " << log2(x1_encrypted_coeff3.scale())
<< " bits" << endl;
evaluator.rescale_to_next_inplace(x1_encrypted_coeff3);
cout << " + Scale of PI*x after rescale: " << log2(x1_encrypted_coeff3.scale())
<< " bits" << endl;
因为x3_encrypted和x1_encrypted_coeff3具有相同的scale和使用相同的加密参数,所以我们可以将它们相乘。我们将结果写入x3_encrypted,relinearize和rescale。再次注意scale是接近2^40,但不完全是2的40次方due to yet another scaling by a prime。我们已经到了模切换链的最后一个level。
print_line(__LINE__);
cout << "Compute, relinearize, and rescale (PI*x)*x^2." << endl;
evaluator.multiply_inplace(x3_encrypted, x1_encrypted_coeff3);
evaluator.relinearize_inplace(x3_encrypted, relin_keys);
cout << " + Scale of PI*x^3 before rescale: " << log2(x3_encrypted.scale())
<< " bits" << endl;
evaluator.rescale_to_next_inplace(x3_encrypted);
cout << " + Scale of PI*x^3 after rescale: " << log2(x3_encrypted.scale())
<< " bits" << endl;
接下来计算1次项。所有这些都需要一个带有plain_coeff1的multiply_plain。我们使用结果覆盖x1_encryption。
print_line(__LINE__);
cout << "Compute and rescale 0.4*x." << endl;
evaluator.multiply_plain_inplace(x1_encrypted, plain_coeff1);
cout << " + Scale of 0.4*x before rescale: " << log2(x1_encrypted.scale())
<< " bits" << endl;
evaluator.rescale_to_next_inplace(x1_encrypted);
cout << " + Scale of 0.4*x after rescale: " << log2(x1_encrypted.scale())
<< " bits" << endl;
继续。
现在我们希望计算所有三项的和。但是,有一个严重的问题:这三个术语所使用的加密参数是不同的,这是由于模量从rescaling而来的。
加密的加法和减法要求输入的level相同,并且加密参数(parms_id)匹配。如果不匹配,Evaluate将抛出异常。
cout << endl;
print_line(__LINE__);
cout << "Parameters used by all three terms are different." << endl;
cout << " + Modulus chain index for x3_encrypted: "
<< context->get_context_data(x3_encrypted.parms_id())->chain_index() << endl;
cout << " + Modulus chain index for x1_encrypted: "
<< context->get_context_data(x1_encrypted.parms_id())->chain_index() << endl;
cout << " + Modulus chain index for plain_coeff0: "
<< context->get_context_data(plain_coeff0.parms_id())->chain_index() << endl;
cout << endl;
让我们仔细考虑一下在这一点上的scales是多少。我们把系数中的质数表示为P_0, P_1, P_2, P_3,按这个顺序。P_3作为特殊的模量,不涉及重调scaling。经过以上规模的计算,密文的scale为:
- Product x^2 has scale 2^80 and is at level 2;
- Product PI*x has scale 2^80 and is at level 2;
- We rescaled both down to scale 2^80/P_2 and level 1;
- Product PI*x^3 has scale (2^80/P_2)^2;
- We rescaled it down to scale (2^80/P_2)^2/P_1 and level 0;
- Product 0.4*x has scale 2^80;
- We rescaled it down to scale 2^80/P_2 and level 1;
- The contant term 1 has scale 2^40 and is at level 2.
虽然这三项的比例大约是2^40,但它们的确切值是不同的,因此不能相加。
print_line(__LINE__);
cout << "The exact scales of all three terms are different:" << endl;
ios old_fmt(nullptr);
old_fmt.copyfmt(cout);
cout << fixed << setprecision(10);
cout << " + Exact scale in PI*x^3: " << x3_encrypted.scale() << endl;
cout << " + Exact scale in 0.4*x: " << x1_encrypted.scale() << endl;
cout << " + Exact scale in 1: " << plain_coeff0.scale() << endl;
cout << endl;
cout.copyfmt(old_fmt);
print_line(__LINE__);
cout << "Normalize scales to 2^40." << endl;
x3_encrypted.scale() = pow(2.0, 40);
x1_encrypted.scale() = pow(2.0, 40);
我们还有一个加密参数不匹配的问题。这是很容易修复,使用传统的模切换(没有重新缩放)。CKKS支持模切换,就像BFV方案一样,允许我们在根本不需要时切换部分系数模量。
print_line(__LINE__);
cout << "Normalize encryption parameters to the lowest level." << endl;
parms_id_type last_parms_id = x3_encrypted.parms_id();
evaluator.mod_switch_to_inplace(x1_encrypted, last_parms_id);
evaluator.mod_switch_to_inplace(plain_coeff0, last_parms_id);
/*三个密文兼容,可加了
All three ciphertexts are now compatible and can be added.
*/
print_line(__LINE__);
cout << "Compute PI*x^3 + 0.4*x + 1." << endl;
Ciphertext encrypted_result;
evaluator.add(x3_encrypted, x1_encrypted, encrypted_result);
//计算结果存入 encrypted_result
evaluator.add_plain_inplace(encrypted_result, plain_coeff0);
/*
First print the true result.
*/
Plaintext plain_result; //明文结果
print_line(__LINE__);
cout << "Decrypt and decode PI*x^3 + 0.4x + 1." << endl;
cout << " + Expected result 希望打印出:" << endl;
vector<double> true_result;
for (size_t i = 0; i < input.size(); i++)
double x = input[i];
true_result.push_back((3.14159265 * x * x + 0.4)* x + 1);
print_vector(true_result, 3, 7);
/* 真正解密、解码、打印 看看如何
Decrypt, decode, and print the result.
*/
decryptor.decrypt(encrypted_result, plain_result); //解密
vector<double> result;
encoder.decode(plain_result, result); //解码
cout << " + Computed result ...... Correct." << endl;
print_vector(result, 3, 7);
虽然我们没有在这些例子中显示任何复数的计算,但是CKKSEncoder可以让我们很容易地做到这一点。复数的加法和乘法就像人们所期望的那样。
运行结果
Microsoft SEAL version: 3.7.1
+---------------------------------------------------------+
| The following examples should be executed while reading |
| comments in associated files in native/examples/. |
+---------------------------------------------------------+
| Examples | Source Files |
+----------------------------+----------------------------+
| 1. BFV Basics | 1_bfv_basics.cpp |
| 2. Encoders | 2_encoders.cpp |
| 3. Levels | 3_levels.cpp |
| 4. CKKS Basics | 4_ckks_basics.cpp |
| 5. Rotation | 5_rotation.cpp |
| 6. Serialization | 6_serialization.cpp |
| 7. Performance Test | 7_performance.cpp |
+----------------------------+----------------------------+
[ 0 MB] Total allocation from the memory pool
> Run example (1 ~ 7) or exit (0): 4
+--------------------------------------+
| Example: CKKS Basics |
+--------------------------------------+
/
| Encryption parameters :
| scheme: CKKS
| poly_modulus_degree: 8192
| coeff_modulus size: 200 (60 + 40 + 40 + 60) bits
\\
Number of slots: 4096
Input vector:
[ 0.0000000, 0.0002442, 0.0004884, ..., 0.9995116, 0.9997558, 1.0000000 ]
Evaluating polynomial PI*x^3 + 0.4x + 1 ...
Line 129 --> Encode input vectors.
Line 140 --> Compute x^2 and relinearize:
+ Scale of x^2 before rescale: 80 bits
Line 152 --> Rescale x^2.
+ Scale of x^2 after rescale: 40 bits
Line 165 --> Compute and rescale PI*x.
+ Scale of PI*x before rescale: 80 bits
+ Scale of PI*x after rescale: 40 bits
Line 180 --> Compute, relinearize, and rescale (PI*x)*x^2.
+ Scale of PI*x^3 before rescale: 80 bits
+ Scale of PI*x^3 after rescale: 40 bits
Line 192 --> Compute and rescale 0.4*x.
+ Scale of 0.4*x before rescale: 80 bits
+ Scale of 0.4*x after rescale: 40 bits
Line 209 --> Parameters used by all three terms are different.
+ Modulus chain index for x3_encrypted: 0
+ Modulus chain index for x1_encrypted: 1
+ Modulus chain index for plain_coeff0: 2
Line 237 --> The exact scales of all three terms are different:
+ Exact scale in PI*x^3: 1099512659965.7514648438
+ Exact scale in 0.4*x: 1099511775231.0197753906
+ Exact scale in 1: 1099511627776.0000000000
Line 262 --> Normalize scales to 2^40.
Line 273 --> Normalize encryption parameters to the lowest level.
Line 282 --> Compute PI*x^3 + 0.4*x + 1.
Line 292 --> Decrypt and decode PI*x^3 + 0.4x + 1.
+ Expected result:
[ 1.0000000, 1.0000977, 1.0001954, ..., 4.5367965, 4.5391940, 4.5415926 ]
+ Computed result ...... Correct.
[ 1.0000000, 1.0000977, 1.0001954, ..., 4.5367995, 4.5391970, 4.5415957 ]
+---------------------------------------------------------+
| The following examples should be executed while reading |
| comments in associated files in native/examples/. |
+---------------------------------------------------------+
| Examples | Source Files |
+----------------------------+----------------------------+
| 1. BFV Basics | 1_bfv_basics.cpp |
| 2. Encoders | 2_encoders.cpp |
| 3. Levels | 3_levels.cpp |
| 4. CKKS Basics | 4_ckks_basics.cpp |
| 5. Rotation | 5_rotation.cpp |
| 6. Serialization | 6_serialization.cpp |
| 7. Performance Test | 7_performance.cpp |
+----------------------------+----------------------------+
[ 51 MB] Total allocation from the memory pool
结语
有关CKKS的源码分析到此为止。后面的篇幅我会分析完5_rotation和6_serialization的代码,分析完后有时间我会专门开一两篇文章来做一些理论知识详解。完成这些工作后我们的SEAL库源码分析也接近尾声了。
以上是关于2021SC@SDUSC-SEAL全同态加密库的主要内容,如果未能解决你的问题,请参考以下文章