蓝桥杯正确的解题姿势

Posted 2023-04-05 兴奋的大公狗

在做算法题的过程中最忌讳的就是上来就一顿乱敲，一开始我就是这样，但随着不断的刷题和老师的指导，总结了自己的刷题方法

示例题目 三角回文数

问题描述
对于正整数 n, 如果存在正整数 k使得 n=1+2+3+...+k=k(k+1)/2 , 则 n 称为三角数。例如, 66066 是一个三角数, 因为 66066=1+2+3+...+363

如果一个整数从左到右读出所有数位上的数字, 与从右到左读出所有数位 上的数字是一样的, 则称这个数为回文数。例如, 66066 是一个回文数, 8778 也是一个回文数。

如果一个整数 nn 既是三角数又是回文数, 我们称它为三角回文数。例如 66066 是三角回文数。

请问, 第一个大于 20220514 的三角回文数是多少?

答案提交
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

运行限制
最大运行时间：1s
最大运行内存: 256M

1. 读题【不着急实现代码，先理清思路】

通过看题，我们能够大致抽象出应该会用到的方法，不管方法多简单，都尽量写一个函数，这样可读性好一些，不要直接在main函数里面实现某个方法，看着就乱。

这道题我们可以总结可能用到的方法如下：
        1.判断是不是回文数 【用双指针法判断】

        2. 从1到k的值 【优化初始值再暴力循环】

        3. 是否满足题中所给的公式 (k*(k+1)/2)=sum 【不需要算法】  

2. 搭架子

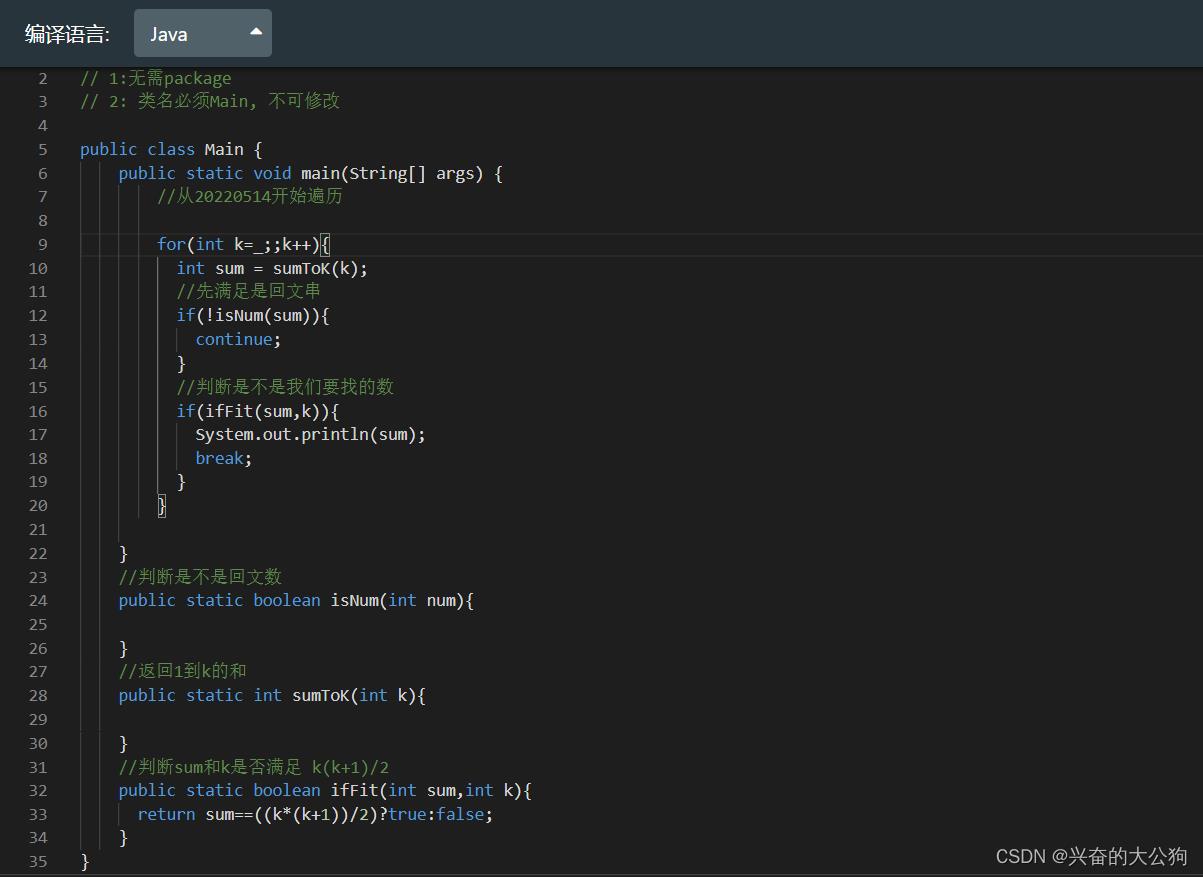
架子搭建好就理理逻辑，看看main函数中的代码逻辑走不走得通

 3. 实现代码

        3.1 双指针法判断回文数【两个指针一个 i 一个 j 两端往中间逼近，不需要考虑字符串是奇数长度还是偶数】

//判断是不是回文数
    public static boolean isNum(int num)
        String val = num+"";
        int i = 0;
        int j = val.length()-1;
        char[] check = val.toCharArray();
        while(i<j)
          if(check[i] != check[j])
            return false;
          
          i++;
          j--;
        
        return true;
    

        3.2 从1加到k优化

public static int sumToK(int k)
      
      for(int i=1;i<=k;i++)
        res += i;
      
      return res;
    

先运行一遍求sumToK(k)比题中给的20220514大的值所对应的k是多少【因为并没有一个sumToK(k) = 202220514】，得到6359，sumToK（6359）=20221620

优化：我们设置初始值为 20221620，这样每次循环就不需要从1加到k了，极大降低时间消耗

public static int sumToK(int k)
      int res = 20221620;
      for(int i=6360;i<=k;i++)
        res += i;
      
      return res;
    

 main函数优化: 我们应该先判断 sumToK(k) 是不是回文串而不是先判断是否满足那个公式，因为这样直接可以过滤一大批不合格的数

完整代码

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main 
    public static void main(String[] args) 
        //从20220514开始遍历
        
        for(int k=6359;;k++)
          int sum = sumToK(k);
          //先满足是回文串
          if(!isNum(sum))
            continue;
          
          //判断是不是我们要找的数
          if(ifFit(sum,k))
            System.out.println(sum);
            break;
          
        

    
    //判断是不是回文数
    public static boolean isNum(int num)
        String val = num+"";
        int i = 0;
        int j = val.length()-1;
        char[] check = val.toCharArray();
        while(i<j)
          if(check[i] != check[j])
            return false;
          
          i++;
          j--;
        
        return true;
    
    //返回1到k的和
    public static int sumToK(int k)
      int res = 20221620;
      for(int i=6360;i<=k;i++)
        res += i;
      
      return res;
    
    //判断sum和k是否满足 k(k+1)/2
    public static boolean ifFit(int sum,int k)
      return sum==((k*(k+1))/2)?true:false;
    

解题报告 之 2015蓝桥杯 垒骰子

解题报告 之 2015蓝桥杯 垒骰子

赌圣 atm 晚年迷恋上了垒骰子，就是把骰子一个垒在还有一个上边。不能歪歪扭扭，要垒成方柱体。

经过长期观察，atm 发现了稳定骰子的奥秘：有些数字的面贴着会互相排斥！
我们先来规范一下骰子：1 的对面是 4。2 的对面是 5，3 的对面是 6。

如果有 m 组相互排斥现象，每组中的那两个数字的面紧贴在一起，骰子就不能稳定的垒起来。

atm 想计算一下有多少种不同的可能的垒骰子方式。

两种垒骰子方式同样，当且仅当这两种方式中相应高度的骰子的相应数字的朝向都同样。
因为方案数可能过多，请输出模 10^9 + 7 的结果。

不要小看了 atm 的骰子数量哦～

「输入格式」
第一行两个整数 n m
n 表示骰子数目
接下来 m 行，每行两个整数 a b。表示 a 和 b 数字不能紧贴在一起。

「输出格式」
一行一个数，表示答案模 10^9 + 7 的结果。

「例子输入」
2 1
1 2

「例子输出」
544

「数据范围」
对于 30% 的数据：n <= 5
对于 60% 的数据：n <= 100
对于 100% 的数据：0 < n <= 10^9, m <= 36

题目大意：略

分析：想当年真是小白啊，，如此简单的题竟然一个字没写。。

太悲慘了。。

依据相关文章一的启示。想把这道题拿出来炒炒陈饭。矩阵高速幂，用一连接矩阵表示各面朝上时能够连接的情况，然后有多少个骰子直接矩阵幂就能够了。

最后注意側面的数字能够转4个情况。则最后再乘一个4^n。注意都要用高速幂来取模。

上代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;
typedef long long ll;
const int MAXN = 8;
const ll MOD = 1e9 + 7;

int n, m;

struct matrix
{
	ll con[MAXN][MAXN];
	matrix()
	{
		for(int i = 0; i < MAXN; i++)
			for(int j = 0; j < MAXN; j++)
				con[i][j] = 0;
	}
};

matrix mul( matrix& a, matrix& b )
{
	matrix ans;
	for(int i = 1; i <= 6; i++)
		for(int j = 1; j <= 6; j++)
			if(a.con[i][j])
				for(int k = 1; k <= 6; k++)
					ans.con[i][k] += a.con[i][j] * b.con[j][k];
	return ans;
}

matrix m_pow( matrix a, int b )
{
	matrix ans;
	for(int i = 1; i <= 6; i++)
		ans.con[i][i] = 1;
	while(b)
	{
		if(b & 1)
			ans = mul( ans, a );
		a = mul( a, a );
		b /= 2;
	}
	return ans;
}

ll q_pow( ll a, ll b, ll c )
{
	ll ans = 1;
	while(b)
	{
		if(b & 1)
		{
			ans = (ans * a) % c;
		}
		b /= 2;
		a = (a*a) % c;
	}
	return ans;
}

int main()
{
//没有找到judge，感觉应该没问题。请各位不吝赐教，多谢！
	matrix ini;
	for(int i = 1; i <= 6; i++)
		ini.con[1][i] = 1;
	matrix con;
	for(int i = 1; i <= 6; i++)
		for(int j = 1; j <= 6; j++)
			con.con[i][j] = 1;

	while(scanf( "%d%d", &n, &m ) == 2)
	{
		int a, b;
		for(int i = 1; i <= m; i++)
		{
			scanf( "%d%d", &a, &b );
			con.con[a][b] = con.con[b][a] = 0;
		}

		ini = mul( ini, m_pow( con, n - 1 ) );
		long long ans = 0;
		for(int i = 1; i <= 6; i++)
		{
			ans += ini.con[1][i];
		}
		ll times = q_pow( 4, n, MOD );
		ans = (ans*times) % MOD;
		printf( "%lld\n", ans );
	}

	return 0;
}