卷积：计算机的眼睛

Posted 2023-04-05 repinkply

现在刷脸支付的场景越来越多，相信人脸识别你一定不陌生，你有没有想过，在计算机识
别人脸之前，我们人类是如何判断一个人是谁的呢？

我们眼睛看到人脸的时候，会先将人脸的一些粗粒度特征提取出来，例如人脸的轮廓、头发的颜色、头发长短等。然后这些信息会一层一层地传入到某一些神经元当中，每经过一层神经元就相当于特征提取。我们大脑最终会将最后的特征进行汇总，类似汇总成一张具体的人脸，用这张人脸去大脑的某一个地方与存好的人名进行匹配。

那落实到我们计算机呢？其实这个过程是一样的，在计算机中进行特征提取的功能，就离不开我们今天要讲的卷积。

可以说，没有卷积的话，深度学习在图像领域不可能取得今天的成就。 那么，就让我们来看看什么是卷积，还有它在 PyTorch 中的实现吧。

卷积

在使用卷积之前，人们尝试了很多人工神经网络来处理图像问题，但是人工神经网络的参数量非常大，从而导致非常难训练，所以计算机视觉的研究一直停滞不前，难以突破。

直到卷积神经网络的出现，它的两个优秀特点：稀疏连接与平移不变性，这让计算机视觉的研究取得了长足的进步。什么是稀疏连接与平移不变性呢？简单来说，就是稀疏连接可以让学习的参数变得很少，而平移不变性则不关心物体出现在图像中什么位置。

稀疏连接与平移不变性是卷积的两个重要特点，如果你想从事计算机视觉相关的工作，这两个特点必须该清楚，但不是这篇文章的重点，这里就不展开了，有兴趣你可以自己去了解。

下面我们直接来看看卷积是如何计算的。

最简单的情况

我们先看最简单的情况，输入是一个 4x4 的特征图，卷积核的大小为 2x2。

卷积核是什么呢？其实就是我们卷积层要学习到的参数，就像下图中红色的示例，下图中的卷积核是最简单的情况，只有一个通道。

 输入特征与卷积核计算时，计算方式是卷积核与输入特征按位做乘积运算然后再求和，其结果为输出特征图的一个元素，下图为计算输出特征图第一个元素的计算方式：

 

完成了第一个元素的计算，我们接着往下看，按以从左向右，从上至下的顺序进行滑动卷积核，分别与输入的特征图进行计算，请看下图，下图为上图计算完毕之后，向右侧滑动一个单元的计算方式：

 第一行第三个单元的计算以此类推。说完了同一行的移动，我们再看看，第一行计算完毕，向下滑动的计算方式是什么样的。

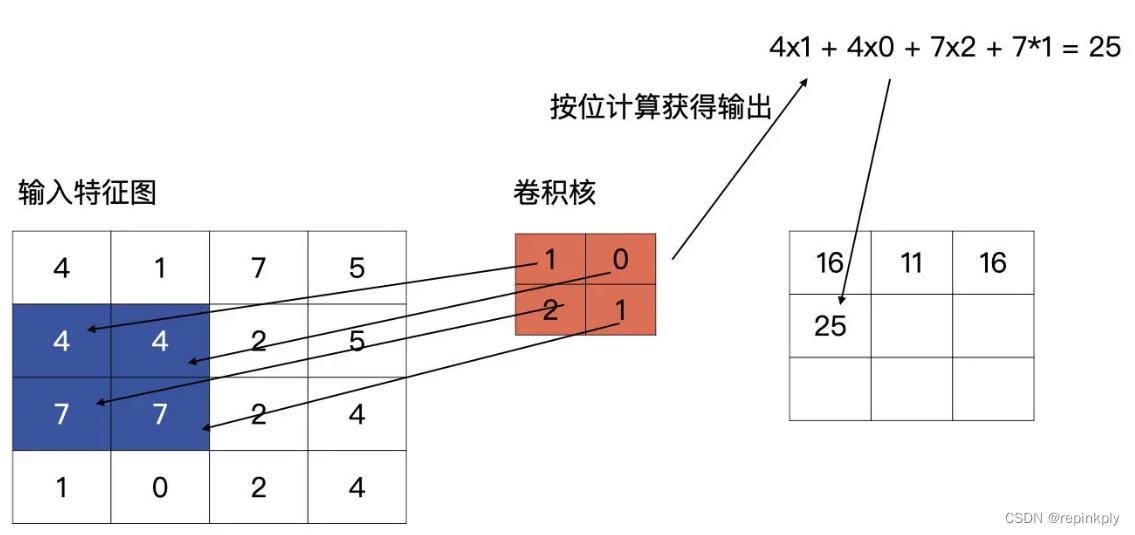
 第一行计算完毕之后，卷积核会回到行首，然后向下滑动一个单元，再重复以上从左至右的滑动计算。

这里我再给你补充一个知识点，什么是步长？

卷积上下左右滑动的长度，我们称为步长，用 stride 表示。上述例子中的步长就是 1，根据问题的不同，会取不同的步长，但通常来说步长为 1 或 2。不管是刚才说的最简单的卷积计算，还是我们后面要讲的标准卷积，都要用到这个参数。

标准的卷积

好啦，前面只是最简单的情况，现在我们将最简单的卷积计算方式延伸到标准的卷积计算方式。

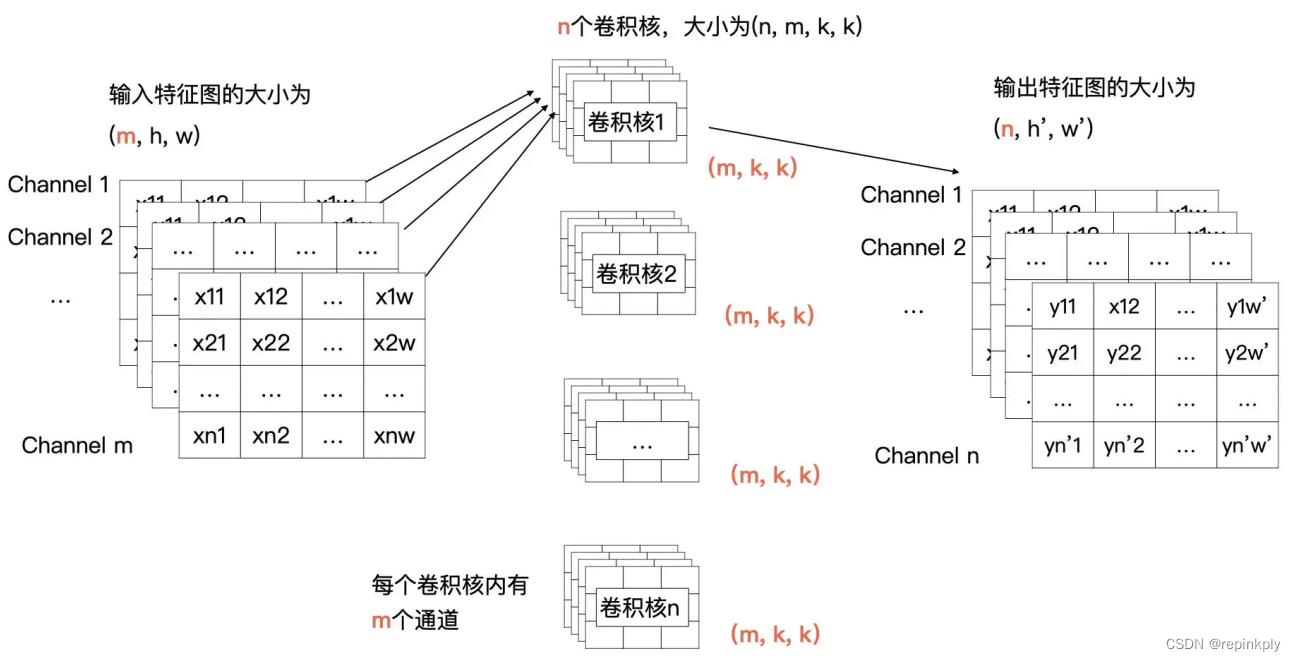
我们先将上面的例子描述为更加通用的形式，输入的特征有 m 个通道，宽为 w，高为 h；输出有 n 个特征图，宽为 w ‘ ，高为 h ’ ；卷积核的大小为 kxk。

在刚才的例子中 m、n、k、w、h、 w ‘ 、 h ’ 的值分别为 1、1、2、4、4、3、3。而现在，我们需要把一个输入为 (m，h，w) 的输入特征图经过卷积计算，生成一个输出为 (n, h ‘ ,w ’ ) 的特征图。

那我们来看看可以获得这个操作的卷积是什么样子的。输出特征图的通道数由卷积核的个数决定的，所以说卷积核的个数为 n。根据卷积计算的定义，输入特征图有 m 个通道，所以每个卷积核里要也要有 m 个通道。所以，我们的需要 n 个卷积核，每个卷积核的大小为(m, k, k)。

为了帮你更好地理解刚才所讲的内容，我画了示意图，你可以对照一下：

 

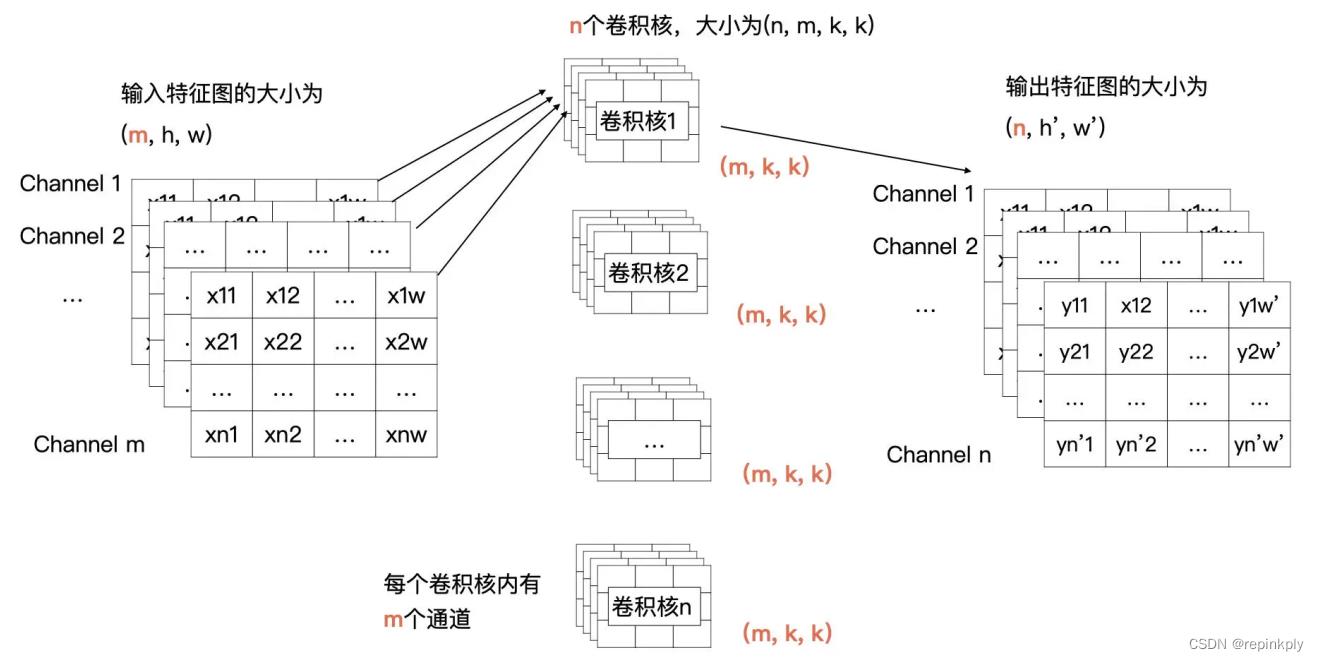
结合上面的图解可以看到，卷积核 1 与全部输入特征进行卷积计算，就获得了输出特征图中第 1 个通道的数据，卷积核 2 与全部输入特征图进行计算获得输出特征图中第 2 个通道的数据。以此类推，最终就能计算 n 个输出特征图。

在开篇的例子中，输入只有 1 个通道，现在有多个通道了，那我们该如何计算呢？其实计算方式类似，输入特征的每一个通道与卷积核中对应通道的数据按我们之前讲过的方式进行卷积计算，也就是输入特征图中第 i 个特征图与卷积核中的第 i 个通道的数据进行卷积。这样计算后会生成 m 个特征图，然后将这 m 个特征图按对应位置求和即可，求和后 m 个特征图合并为输出特征中一个通道的特征图。

我们可以用后面的公式表示当输入有多个通道时，每个卷积核是如何与输入进行计算的。

Output i 表示计算第 i 个输出特征图，i 的取值为 1 到 n；

kernel k 表示 1 个卷积核里的第 k 个通道的数据；

input k 表示输入特征图中的第 k 个通道的数据；

bias k 为偏移项，我们在训练时一般都会默认加上；

⋆ 为卷积计算；

Output i = ∑ kernel k ⋆ input k + bias i ,
i = 1, 2, … , n

我来解释一下为什么要加 bias。就跟回归方程一样，如果不加 bias 的话，回归方程为y=wx 不管 w 如何变化，回归方程都必须经过原点。如果加上 bias 的话，回归方程变为y=wx+b，这样就不是必须经过原点，可以变化的更加多样。

好啦，卷积计算方式的讲解到这里就告一段落了。下面我们看看在卷积层中有关卷积计算
的另外一个重要参数。

Padding

让我们回到开头的例子，可以发现，输入的尺寸是 4x4，输出的尺寸是 3x3。你有没有发现，输出的特征图变小了？没错，在有多层卷积层的神经网络中，特征图会越来越小。

但是，有的时候我们为了让特征图变得不是那么小，可以对特征图进行补零操作。这样做主要有两个目的：

1. 有的时候需要输入与输出的特征图保持一样的大小；
2. 让输入的特征保留更多的信息。

这里我举个例子，带你看看，一般什么情况下会希望特征图变得不那么小。

通过刚才的讲解我们知道，如果不补零且步长（stride）为 1 的情况下，当有多层卷积层时，特征图会一点点变小。如果我们希望有更多层卷积层来提取更加丰富的信息时，就可以让特征图变小的速度稍微慢一些，这个时候就可以考虑补零。

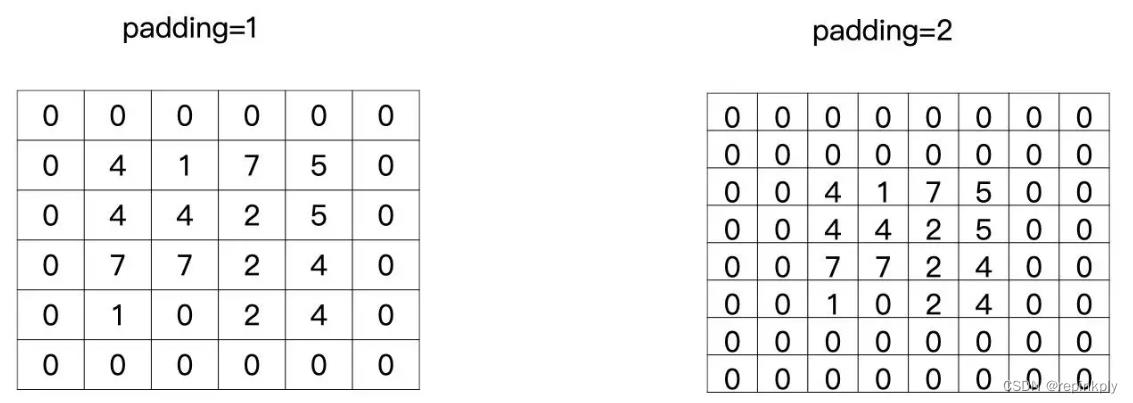
这个补零的操作就叫做 padding，padding 等于 1 就是补一圈的零，等于 2 就是补两圈的零，如下图所示：

 

在 Pytorch 中，padding 这个参数可以是字符串、int 和 tuple。

我们分别来看看不同参数类型怎么使用：当为字符串时只能取’valid’与’same’。当给定整型时，则是说要在特征图外边补多少圈 0。如果是 tuple 的时候，则是表示在特征图的行与列分别指定补多少零。

我们重点看一下字符串的形式，相比于直接给定补多少零来说，我认为字符串更加常用。其中，'valid’就是没有 padding 操作，就像开头的例子那样。'same’则是让输出的特征图与输入的特征图获得相同的大小。

那当 padding 为 same 时，到底是怎么计算的呢？我们继续用开篇的例子说明，现在padding 为’same’了。

 

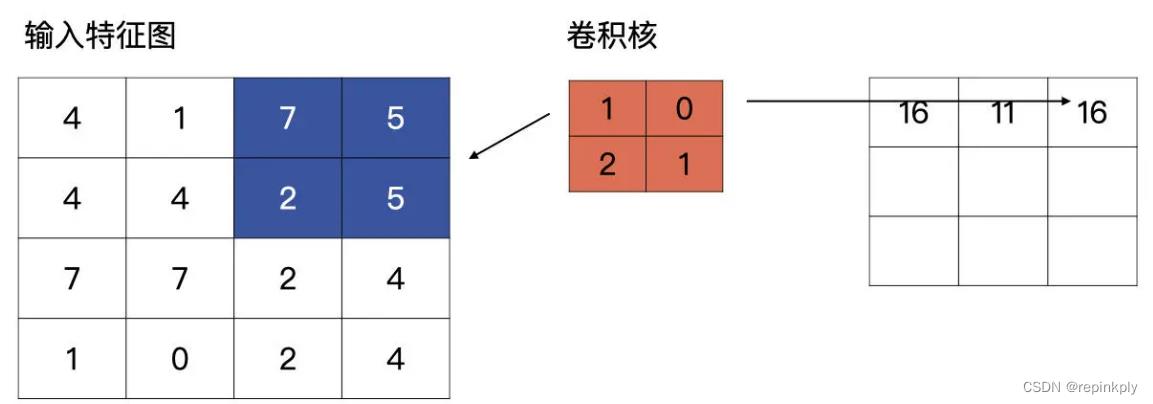
当滑动到特征图最右侧时，发现输出的特征图的宽与输入的特征图的宽不一致，它会自动补零，直到输出特征图的宽与输入特征图的宽一致为止。如下图所示：

 

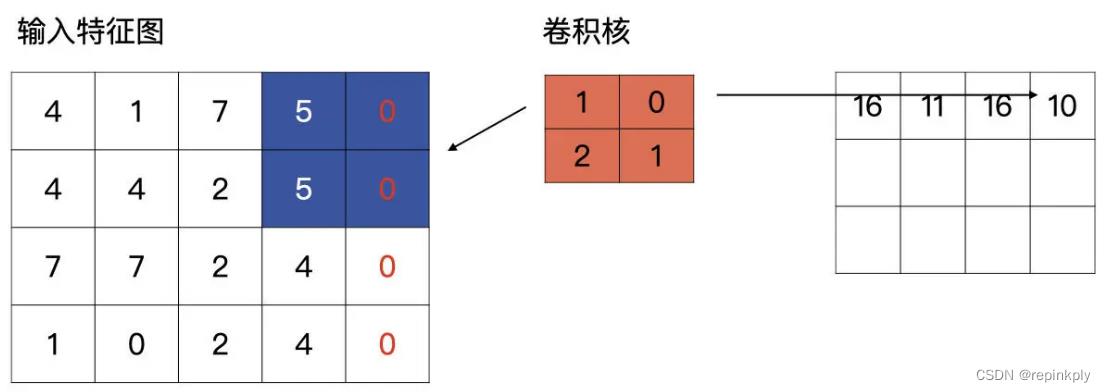
高的计算和宽的计算同理，当计算到特征图的底部时，发现输出特征图的高与输入特征图的高不一致时，它同样会自动补零，直到输入和输出一致为止，如下图所示。

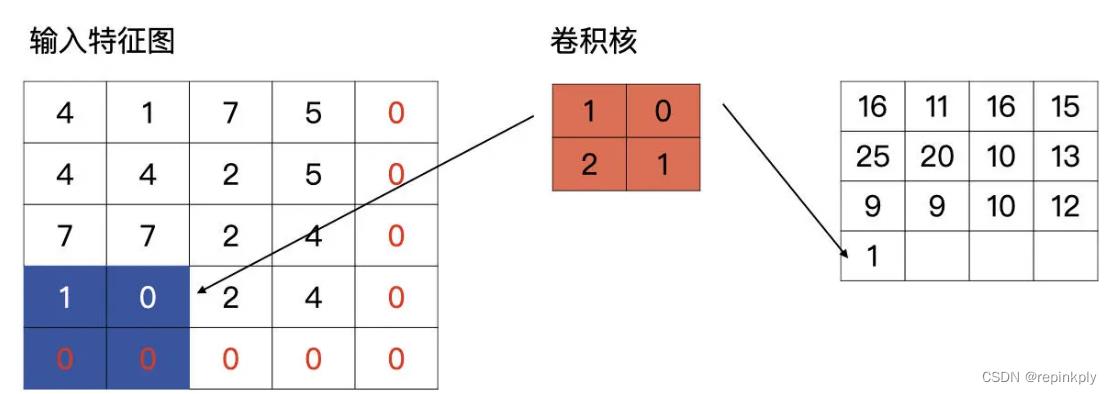
 完成上述操作，我们就可以获得与输入特征图有相同高、宽的输出特征图了。理论讲完了，我们还是要学以致用，在实践中深入体会。在下面的练习中，我们会实际考察一下当padding 为 same 时，是否像我们说的这样计算。

PyTorch 中的卷积

卷积操作定义在 torch.nn 模块中，torch.nn 模块为我们提供了很多构建网络的基础层与方法。

在 torch.nn 模块中，关于今天介绍的卷积操作有 nn.Conv1d、nn.Conv2d 与nn.Conv3d 三个类。

请注意，我们上述的例子都是按照 nn.Conv2d 来介绍的，nn.Conv2d 也是用的最多的，而 nn.Conv1d 与 nn.Conv3d 只是输入特征图的维度有所不一样而已，很少会被用到。

让我们先看看创建一个 nn.Conv2d 需要哪些必须的参数：

# Conv2d类
class torch.nn.Conv2d(in_channels,
     out_channels,
     kernel_size,
     stride=1,
     padding=0,
     dilation=1,
     groups=1,
     bias=True,
     padding_mode='zeros',
     device=None,
     dtype=None)

我们挨个说说这些参数。首先是跟通道相关的两个参数：in_channels 是指输入特征图的通道数，数据类型为 int，在标准卷积的讲解中 in_channels 为 m；out_channels 是输出特征图的通道数，数据类型为 int，在标准卷积的讲解中 out_channels 为 n。

kernel_size 是卷积核的大小，数据类型为 int 或 tuple，需要注意的是只给定卷积核的高与宽即可，在标准卷积的讲解中 kernel_size 为 k。

stride 为滑动的步长，数据类型为 int 或 tuple，默认是 1，在前面的例子中步长都为 1。

padding 为补零的方式，注意当 padding 为’valid’或’same’时，stride 必须为1。

对于 kernel_size、stride、padding 都可以是 tuple 类型，当为 tuple 类型时，第一个维度用于 height 的信息，第二个维度时用于 width 的信息。

bias 是否使用偏移项。

还有两个参数：dilation 与 groups，具体内容下面我们继续展开讲解，你先有个印象就行。

验证 same 方式

接下来，我们做一个练习，验证 padding 为 same 时，计算方式是否像我们所说的那样。过程并不复杂，一共三步，分别是创建输入特征图、设置卷积以及输出结果。

先来看第一步，我们创建好例子中的（4，4，1）大小的输入特征图，代码如下：

import torch
import torch.nn as nn
input_feat = torch.tensor([[4, 1, 7, 5], [4, 4, 2, 5], [7, 7, 2, 4], [1, 0, 2,1]])
print(input_feat)
print(input_feat.shape)

# 输出：
tensor([[4., 1., 7., 5.],
[4., 4., 2., 5.],
[7., 7., 2., 4.],
[1., 0., 2., 4.]])

torch.Size([4, 4])

第二步，创建一个 2x2 的卷积，根据刚才的介绍，输入的通道数为 1，输出的通道数为1，padding 为’same’，所以卷积定义为：

conv2d = nn.Conv2d(1, 1, (2, 2), stride=1, padding='same', bias=True)
# 默认情况随机初始化参数
print(conv2d.weight)
print(conv2d.bias)
# 输出：
Parameter containing:
tensor([[[[ 0.3235, -0.1593],
[ 0.2548, -0.1363]]]], requires_grad=True)
Parameter containing:
tensor([0.4890], requires_grad=True)

需要注意的是，默认情况下是随机初始化的。一般情况下，我们不会人工强行干预卷积核的初始化，但是为了验证今天的例子，我们对卷积核的参数进行干预。请注意下面代码中卷积核的注释，代码如下：

conv2d = nn.Conv2d(1, 1, (2, 2), stride=1, padding='same', bias=False)
# 卷积核要有四个维度(输入通道数，输出通道数，高，宽)
kernels = torch.tensor([[[[1, 0], [2, 1]]]], dtype=torch.float32)
conv2d.weight = nn.Parameter(kernels, requires_grad=False)
print(conv2d.weight)
print(conv2d.bias)
# 输出：
Parameter containing:
tensor([[[[1., 0.],
[2., 1.]]]])
None

完成之后就进入了第三步，现在我们已经准备好例子中的输入数据与卷积数据了，下面只需要计算一下，然后输出就可以了，代码如下：

output = conv2d(input_feat)
2 ---------------------------------------------------------------------------
3 RuntimeError
Traceback (most recent call last)
4 /var/folders/pz/z8t8232j1v17y01bkhyrl01w0000gn/T/ipykernel_29592/2273564149.py
5 ----> 1 output = conv2d(input_feat)
6 ~/Library/Python/3.8/lib/python/site-packages/torch/nn/modules/module.py in _c
7 1049
8 1050
9 -> 1051
if not (self._backward_hooks or self._forward_hooks or self._f
or _global_forward_hooks or _global_forward_pre_hooks)
return forward_call(*input, **kwargs)
10 1052 # Do not call functions when jit is used
11 1053 full_backward_hooks, non_full_backward_hooks = [], []
12 ~/Library/Python/3.8/lib/python/site-packages/torch/nn/modules/conv.py in forw
13 441
14 442
15 --> 443
def forward(self, input: Tensor) -> Tensor:
return self._conv_forward(input, self.weight, self.bias)
16 444
17 445 class Conv3d(_ConvNd):
18 ~/Library/Python/3.8/lib/python/site-packages/torch/nn/modules/conv.py in _con
19 437
20 438
21 --> 439
22 440
23 441
weight, bias, self.stride,
_pair(0), self.dilation, self.groups)
return F.conv2d(input, weight, bias, self.stride,
self.padding, self.dilation, self.groups)

结合上面代码，你会发现这里报错了，提示信息是输入的特征图需要是一个 4 维的，而我们的输入特征图是一个 4x4 的 2 维特征图。这是为什么呢？

请你记住，Pytorch 输入 tensor 的维度信息是 (batch_size, 通道数，高，宽)，但是在我们的例子中只给定了高与宽，没有给定 batch_size（在训练时，不会将所有数据一次性加载进来训练，而是以多个批次进行读取的，每次读取的量成为 batch_size）与通道数。所以，我们要回到第一步将输入的 tensor 改为 (1,1,4,4) 的形式。

你还记得我在之前的讲解中提到过怎么对数组添加维度吗？

在 Pytorch 中 unsqueeze() 对 tensor 的维度进行修改。代码如下：

input_feat = torch.tensor([[4, 1, 7, 5], [4, 4, 2, 5], [7, 7, 2, 4], [1,
0, 2,4])
print(input_feat)
print(input_feat.shape)
# 输出：
tensor([[[[4., 1., 7., 5.],
[4., 4., 2., 5.],
[7., 7., 2., 4.],
[1., 0., 2., 4.]]]])
torch.Size([1, 1, 4, 4])

这里，unsqueeze() 中的参数是指在哪个位置添加维度。

好，做完了修改，我们再次执行代码。

output = conv2d(input_feat)
tensor([[[[16., 11., 16., 15.],
[25., 20., 10., 13.],
[ 9.,, 10., 12.],
[ 1.,0.,2.,4.]]]])

你可以看看，跟我们在例子中推导的结果一不一样？

小结

今天所讲的卷积非常重要，它是各种计算机视觉应用的基础，例如图像分类、目标检测、图像分割等。

卷积的计算方式是你需要关注的重点。具体过程如下图所示，输出特征图的通道数由卷积核的个数决定的，下图中因为有 n 个卷积核，所以输出特征图的通道数为 n。输入特征图有 m 个通道，所以每个卷积核里要也要有 m 个通道。

 其实卷积背后的理论比较复杂，但在 PyTorch 中实现却很简单。在卷积计算中涉及的几大要素：输入通道数、输出通道数、步长、padding、卷积核的大小，分别对应的就是PyTorch 中 nn.Conv2d 的关键参数。所以，就像前面讲的那样，我们要熟练用好nn.Conv2d()。

你的计算机也可以看懂世界——十分钟跑起卷积神经网络（Windows+CPU）

写这篇文章，我的希望是能让非计算机专业的同学能够基于Caffe这个框架运行起来一个神经网络

众所周知，如果你想研究Deep Learning，那么比较常用的配置是Linux+GPU，不过现在很多非计算机专业的同学有时也会想采用Deep Learning方法来完成一些工作，那么Linux+GPU的环境就有可能会给他们带来一定困扰，我写这篇文章就是为了让这些同学可以不用去装Linux系统，不用去涉及GPU，就可以基于Caffe框架跑出一个简单的神经网络。

 

CNN基础知识：https://zhuanlan.zhihu.com/p/22038289?refer=intelligentunit（没基础的还应该另外了解一些神经网络算法的基础知识，例如前馈传递，BP算法等，有基础的也推荐再通过这个链接巩固一番，以下的文章会假设你对于CNN有比较全面和扎实的理解）

所需系统环境：windows7 sp1及以上系统，win7 sp1以下的会不会有什么错误我不知道，对了，是64位系统哦~

其他环境：Visual Studio 2013，cygwin 2.871（其他版本应该也可以，主要是用来在windows系统上模拟一个非常简易的linux环境，因为应用上只会用到一些很基础的命令，所以早一点的版本也无所谓）

Windows版Caffe框架：https://github.com/Microsoft/caffe

首先，需要将windows版本的Caffe框架下载到本地，随便下到哪都行，然后随便解压缩到哪都行，我解压完之后，Caffe框架的根目录就是H:\\caffe-master\\caffe-master。解压完之后，我们可以很明显地发现，这个框架还是一块未编译的“生肉”，是不能直接使用的，所以我们需要利用VS2013对其进行编译，但是在此之前，还有一个步骤，因为我们是小穷逼，我们没有动辄上万的GPU，但是贾大神所在的土豪实验室有用不完的GPU，所以这里默认的还是GPU模式的框架，我们需要对这一点进行修改，具体方式就是修改根目录中windows文件夹中的CommonSettings.props.example文件，具体修改方式是：

一、将该文件重命名为CommonSettings.props；

二、将该文件中的

<CpuOnlyBuild>false</CpuOnlyBuild>
<UseCuDNN>true</UseCuDNN>

改为

<CpuOnlyBuild>true</CpuOnlyBuild>
<UseCuDNN>false</UseCuDNN>

至于这里面的CuDNN是什么，之后会提到，现在先不用了解~

三、保存该文件。

在将框架改为CPU模式之后，就可以双击打开windows文件夹中的Caffe.sln文件，然后在VS2013中点击最上方的生成->重新生成解决方案即可，需要注意的是，进行这一步之前最好将Debug模式改成Release，就像这样。

经过一段时间的编译，在VS2013下端的显示台上会显示生成成功的信息，这时候这个框架就编译完成了，而生成的可执行文件caffe.exe的位置在根目录中的Build\\x64\\Release之中，同时还会生成一大堆的依赖包和各类库，这里各位先不用在意，今天的任务主要会和caffe.exe发生接触。

编译好了框架之后，可以说是万事俱备，只欠数据集和网络模型了，在第一次的尝试中，CSDN的卜居大神所推崇的使用Yann LeCun大神（我习惯于说成杨乐村大神）提出的LeNet-5网络模型来进行对MNIST数据集的学习是非常适合的。

MNIST数据集是一个手写数字的数据库，所以可想而知，这次训练的目的是让你的计算机学会“看懂数字”。

MNIST数据集在哪里获取呢？Caffe框架已经为你想到了这一点，所以在H:\\caffe-master\\caffe-master\\data\\mnist中的get_mnist.sh脚本就是用来帮你下载这个数据集的，理论上，这个脚本的运行需要Linux的环境支持，但是我们现在用的是windows环境，怎么办呢？很简单，还记得之前所说的cygwin吗？没错，就用它！有关cygwin的安装和配置可以看看这个http://www.cygwin.cn/site/install/。

现在，你已经安装好了cygwin，并已经将其双击打开，只需要在这个黑框框里如下输入，然后回车，就会为你自动下载MNIST数据集（注意，如果不FQ是没有办法下载的，推荐一下我一直用的Psiphon3，这个名字一搜就能搜到，你们懂的）。

 

（忽略我的电脑名字是Celia，用的实验室的机器，懒得改了。。。）

这时候，你会发现在data\\mnist文件夹中出现了

 

，也就是说，MNIST数据集已经成功地下载下来了。

那么这个数据集是不是可以直接用了呢？答案是不能。为什么呢？因为到这一步为止，我们的数据集还只是二进制文件，需要转换为lmdb文件才可以被Caffe框架识别，所以这其中还有一个转换的过程，对于windows用户来说，这个转换是比较烦的，以至于我自己也没有试过，但是由于我之前一直在Ubuntu系统中使用这个框架，所以我们可以采用如下的两种方法：

一、在Ubuntu系统中，首先cd进Caffe框架的根目录，之后只需通过简单的一行命令：

./examples/mnist/create_mnist.sh

即可完成数据的转换工作，那么因为这里我们不希望去使用Ubuntu，所以我比较推荐第二种方法。

二、去网上找资源。。。MNIST数据集的lmdb文件在网上是容易找到的，这里我也用我的网盘分享了一份，http://pan.baidu.com/s/1o86O7Xo。

假设你是从我的网盘下载的，那么现在只需要把这个下载下来的文件解压，然后把解压出来的mnist_train_lmdb以及mnist_test_lmdb文件夹放到examples/mnist中即可。

至于我们使用的LeNet-5模型，眼尖的同学应该已经发现了，早就已经存在于examples/mnist文件夹中了。

现在，我们有了框架，有了数据集，有了模型，那么就快要大功告成了。接下来，只需要在windows自带的cmd命令行界面中如下输入：

 

之后按下回车，就大功告成啦，只需在黑框框中不断跳文字的过程中静静地等待即可。。。这个训练时间主要和你的计算机的配置有关，训练完成时的状态是这样的：

 

可以看到，最终的正确率达到了惊人的99.09%，而损失也降到了0.026495。通过训练之后生成的权重也保存在了mnist文件夹中的lenet_iter_10000.caffemodel之中。这时候，我们可以通过训练好的模型来对测试集进行测试。测试所需代码如下：

 

最后，我们可以发现这个模型在测试集上的正确率达到了非常惊人的程度。

 

这样，我们就可以说，你的计算机上成功地诞生了神经网络，而你的计算机同时也成功学会了“认识数字”。

 

备注：本人非常乐意分享我的文章，转载请注明我的博客地址：http://www.cnblogs.com/matthewli/与原文地址：http://www.cnblogs.com/matthewli/p/6048907.html，谢谢！