蓝桥杯DFS正确入门方式 | DFS + 递归与递推习题课(上) | 一节课教你爆搜!——学习笔记
Posted 小卢先冲
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了蓝桥杯DFS正确入门方式 | DFS + 递归与递推习题课(上) | 一节课教你爆搜!——学习笔记相关的知识,希望对你有一定的参考价值。
目录
同系列文章——传送门
【蓝桥杯】DFS深度优先练习题——基础入门模板(1)_小卢先冲的博客-CSDN博客第一题:递归实现指数型枚举、第二题:全排列问题、第三题:组合的输出
https://blog.csdn.net/weixin_61082895/article/details/129874100?spm=1001.2014.3001.5501
【蓝桥杯】DFS正确入门方式 | DFS + 递归与递推习题课(下) | 一节课教你爆搜!——学习笔记_小卢先冲的博客-CSDN博客第一题:入门迷宫问题、第二题:[USACO10OCT]Lake Counting S洪水灌溉问题、第三题:棋盘问题、第四题:[NOIP2001 提高组] 数的划分
https://blog.csdn.net/weixin_61082895/article/details/129912846
DFS正确入门方式 | DFS + 递归与递推习题课(上) | 一节课教你爆搜!_哔哩哔哩_bilibili
大佬的教学视频非常细!
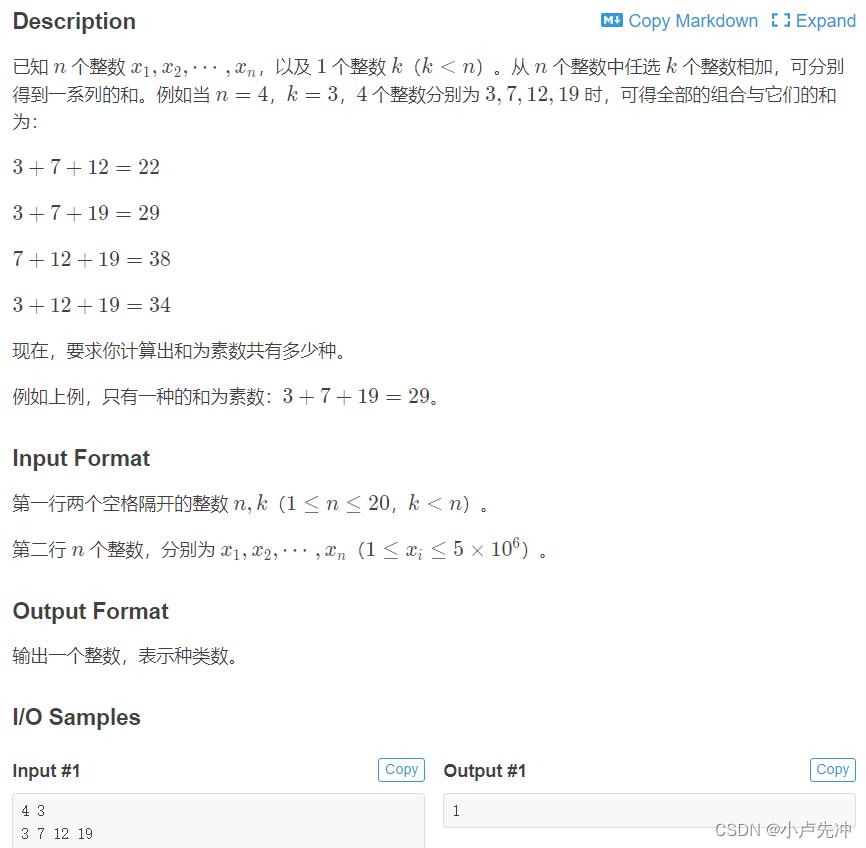
第一题:[NOIP2002 普及组] 选数
题目描述
题目分析
dfs模板题 (组合型模板3)——枚举的每一个数之间相互影响即选了3,后一个位置就不能再选3了
思路:依次枚举每个位置放哪个数
优化代码(剪枝)
题目代码
import java.util.Scanner; public class 选数_dfs static int n, k; static int arr[];//存数据 static int st[];//存答案 static int res;//存种类数 public static void main(String[] args) st = new int[25]; arr = new int[25]; Scanner sca = new Scanner(System.in); n = sca.nextInt(); k = sca.nextInt(); for (int i = 1; i <= n; i++) arr[i] = sca.nextInt(); dfs(1, 1); System.out.println(res); static void dfs(int x, int start) //x:枚举到第几个位置 start:枚举到这个位置从几开始 if((x-1)+(n-start+1)<k)//剪枝,填不满k个数的时候直接剪支(优化代码) return; if (x > k) int sum = 0; for (int i = 1; i <= k; i++) sum += st[i]; if (isprime(sum)) //如果是素数种类数+1 res++; for (int i = start; i <= n; i++) st[x] = arr[i]; dfs(x + 1, i + 1);//继续向下,深度优先 st[x] = 0;//恢复现场 static Boolean isprime(int sum) //判断素数 if (sum < 2) return false; for (int i = 2; i <= sum / i; i++) //i*i可能会溢出int 所以在数值很大的时候写成 if (sum % i == 0) return false; return true;用java写的代码不能通过所有案列
第二题: 烤鸡
题目背景
猪猪 Hanke 得到了一只鸡。
题目描述
猪猪 Hanke 特别喜欢吃烤鸡(本是同畜牲,相煎何太急!)Hanke 吃鸡很特别,为什么特别呢?因为他有 10 种配料(芥末、孜然等),每种配料可以放 1 到 3 克,任意烤鸡的美味程度为所有配料质量之和。
现在, Hanke 想要知道,如果给你一个美味程度 n ,请输出这 10 种配料的所有搭配方案。
输入格式
一个正整数 n,表示美味程度。
输出格式
第一行,方案总数。
第二行至结束,10 个数,表示每种配料所放的质量,按字典序排列。
如果没有符合要求的方法,就只要在第一行输出一个 0。
输入输出样例
输入
11输出
10 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1说明/提示
对于 100% 的数据n≤5000。
题目分析
依次枚举每种调料可以放几克 (指数级枚举模板1)——枚举的每一种调料相互不影响
题目代码
import java.util.Scanner; public class 烤鸡 static int n, res; static int[] arr;//存答案 static int mem[][];//存所有方案 public static void main(String[] args) Scanner sca = new Scanner(System.in); n = sca.nextInt(); arr = new int[20];//开辟空间的时候一般都多一点 mem = new int[59055][20];//总共有3^10种方案,你不清楚你最后有几种可行方案所以要开辟最大的空间 dfs(1, 0); System.out.println(res); for (int i = 1; i <=res ; i++) for (int j = 1; j <=10 ; j++) System.out.print(mem[i][j]); System.out.println(); static void dfs(int x, int sum) if (sum > n) //超过目标质量——剪枝 return; if (x > 10) //说明前10个位置都选好了 if (sum == n) res++;//种类+1 for (int i = 1; i <= 10; i++) //为每一种方案赋值 mem[res][i] = arr[i]; return; for (int i = 1; i <= 3; i++) //3种质量选法 1/2/3 arr[x] = i; // sum += i;//调料质量 不能这么写,因为每当一次枚举完返回到上一个位置枚举的时候sum应该是上一次的不能改变 dfs(x + 1, sum + i); arr[x] = 0;//恢复现场
第三题:[NOIP2004 普及组] 火星人
题目描述
人类终于登上了火星的土地并且见到了神秘的火星人。人类和火星人都无法理解对方的语言,但是我们的科学家发明了一种用数字交流的方法。这种交流方法是这样的,首先,火星人把一个非常大的数字告诉人类科学家,科学家破解这个数字的含义后,再把一个很小的数字加到这个大数上面,把结果告诉火星人,作为人类的回答。
火星人用一种非常简单的方式来表示数字――掰手指。火星人只有一只手,但这只手上有成千上万的手指,这些手指排成一列,分别编号为 1,2,3,⋯。火星人的任意两根手指都能随意交换位置,他们就是通过这方法计数的。
一个火星人用一个人类的手演示了如何用手指计数。如果把五根手指――拇指、食指、中指、无名指和小指分别编号为 1,2,3,4和 5,当它们按正常顺序排列时,形成了 5 位数 12345,当你交换无名指和小指的位置时,会形成 55 位数 1235412354,当你把五个手指的顺序完全颠倒时,会形成 54321,在所有能够形成的 120 个 5 位数中,12345 最小,它表示 1;12354 第二小,它表示 2;54321 最大,它表示 120。下表展示了只有 3 根手指时能够形成的 6 个 3 位数和它们代表的数字:
三进制数 代表的数字 123 1 132 2 213 3 231 4 312 5 321 6 现在你有幸成为了第一个和火星人交流的地球人。一个火星人会让你看他的手指,科学家会告诉你要加上去的很小的数。你的任务是,把火星人用手指表示的数与科学家告诉你的数相加,并根据相加的结果改变火星人手指的排列顺序。输入数据保证这个结果不会超出火星人手指能表示的范围。
输入格式
共三行。
第一行一个正整数 N,表示火星人手指的数目(1≤N≤10000)。
第二行是一个正整数 M,表示要加上去的小整数(1≤M≤100)。
下一行是 1 到 N 这 N 个整数的一个排列,用空格隔开,表示火星人手指的排列顺序。输出格式
N 个整数,表示改变后的火星人手指的排列顺序。每两个相邻的数中间用一个空格分开,不能有多余的空格。
输入输出样例
输入
5 3 1 2 3 4 5输出
1 2 4 5 3说明/提示
对于 30%的数据,N≤15。
对于 60% 的数据,N≤50。
对于 100% 的数据,N≤10000。
noip2004 普及组第 4 题
题目分析
dfs模板题 (全排列型模板2)——枚举的每一个数之间相互影响即选了3,后一个位置就不能再选3了
思路:依次枚举每个位置放哪个数
注意当找到答案时就返回 不然数据太大会超时
题目代码
import java.util.Scanner; public class 火星人_dfs static int n, m, res; static Boolean st[];//false表示没有选这个数,true表示选了这个数 static int arr[];//存答案 static int mars[]; static Boolean log = false; public static void main(String[] args) st = new Boolean[10005]; arr = new int[10005]; mars = new int[10005]; Scanner sca = new Scanner(System.in); //输入 n = sca.nextInt(); m = sca.nextInt(); for (int i = 1; i <= n; i++) mars[i] = sca.nextInt(); st[i] = false; dfs(1); static void dfs(int x) if (x > n) res++;//种类+1 if (res == m + 1) for (int i = 1; i <= n; i++) System.out.print(arr[i] + " "); log = true; return; for (int i = 1; i <= n; i++) if (log) return;//找到答案就不用继续搜索了,数据太大的话会超时 if (res == 0) i = mars[x];//从火星人给的数据开始枚举 if (!st[i]) //这个数没有被选 st[i] = true; arr[x] = i; dfs(x + 1); arr[x] = 0;//恢复现场 st[i] = false;
第四题: [NOIP2008 提高组] 火柴棒等式
题目描述
给你 n 根火柴棍,你可以拼出多少个形如A+B=C 的等式?等式中的 A、B、C 是用火柴棍拼出的整数(若该数非零,则最高位不能是 0)。用火柴棍拼数字0∼9 的拼法如图所示:
注意:
加号与等号各自需要两根火柴棍;
如果 A=B,则A+B=C 与B+A=C 视为不同的等式(A,B,C≥0);
n 根火柴棍必须全部用上。
输入格式
一个整数 (1≤n≤24)。
输出格式
一个整数,能拼成的不同等式的数目。
输入输出样例
输入
14输出
2输入
18输出
9说明/提示
【输入输出样例 1 解释】
2 个等式为 0+1=1 和 1+0=1
【输入输出样例 2 解释】
9 个等式为
0+4=4、0+11=11、1+10=11、2+2=4、2+7=9、4+0=4、7+2=9、10+1=11、11+0=11。
题目分析
dfs模板题 (组合型模板3)
注意:本题每个数是可以重复取的
思路:依次枚举每个位置放哪个数
满足俩个条件:A+B=C、A+B+C的火柴棍=n-4
题目代码
import java.util.Scanner; public class 火柴棒等式_dfs static int n, res; static int arr[];//存答案 static int nums[] = 6, 2, 5, 5, 4, 5, 6, 3, 7, 6;//每一个数字需要火柴棍的数量 public static void main(String[] args) arr = new int[10000]; Scanner sca = new Scanner(System.in); n = sca.nextInt(); n = n - 4;//减去符号需要的4个火柴棍 dfs(1, 0); System.out.println(res); static void dfs(int x, int sum) if (sum > n) return;//剪枝 if (x > 3) if ((arr[1] + arr[2] == arr[3]) && sum == n) res++;//种类数加1 return; for (int i = 0; i <= 1000; i++) //从0开始选数 arr[x] = i; dfs(x + 1, sum+col(i)); arr[x] = 0;//恢复现场 static int col(int n) //计算每一个数需要的火柴棍数量 int sumFire = 0; if (n==0) sumFire += nums[0]; while (n != 0) sumFire += nums[n % 10]; n /= 10; return sumFire;
第五题:PERKET
题目描述
Perket 是一种流行的美食。为了做好 Perket,厨师必须谨慎选择食材,以在保持传统风味的同时尽可能获得最全面的味道。你有 n 种可支配的配料。对于每一种配料,我们知道它们各自的酸度 s 和苦度 b。当我们添加配料时,总的酸度为每一种配料的酸度总乘积;总的苦度为每一种配料的苦度的总和。
众所周知,美食应该做到口感适中,所以我们希望选取配料,以使得酸度和苦度的绝对差最小。
另外,我们必须添加至少一种配料,因为没有任何食物以水为配料的。
输入格式
第一行一个整数 n,表示可供选用的食材种类数。
接下来 n 行,每行 2 个整数 si 和 bi,表示第 i 种食材的酸度和苦度。
输出格式
一行一个整数,表示可能的总酸度和总苦度的最小绝对差。
输入输出样例
输入 #1复制
1 3 10输出 #1复制
7输入 #2复制
2 3 8 5 8输出 #2复制
1输入 #3复制
4 1 7 2 6 3 8 4 9输出 #3复制
1说明/提示
数据规模与约定
对于 100%的数据,有 1≤n≤10,且将所有可用食材全部使用产生的总酸度和总苦度小于 1×10^9,酸度和苦度不同时为 1 和 0。
题目分析
dfs模板题 (指数枚举型模板1)
思路:依次枚举每种调料选与不选
本题需要注意的是:必须添加至少一种配料
题目代码
import java.util.Scanner; public class PERKET_dfs static int n; static int[] acid; static int[] bitter; static int st[];//0表示还没有考虑到,1表示选了这个数,2表示没有选这个数 static int res = Integer.MAX_VALUE;//存答案 public static void main(String[] args) Scanner sca = new Scanner(System.in); n = sca.nextInt(); st = new int[15]; acid = new int[15]; bitter = new int[15]; for (int i = 1; i <= n; i++) acid[i] = sca.nextInt(); bitter[i] = sca.nextInt(); dfs(1); System.out.println(res); static void dfs(int x) if (x > n) Boolean log = false;//表示一种调料没选 int sum_acid = 1;//酸度之积 int sum_bitter = 0;//苦度之和 for (int i = 1; i <= n; i++) if (st[i] == 1) log = true; sum_acid *= acid[i]; sum_bitter += bitter[i]; if (log) res = Math.min(res, Math.abs(sum_acid - sum_bitter)); return; st[x] = 1;//选 dfs(x + 1); st[x] = 0;//恢复现场 st[x] = 2;//不选 dfs(x + 1); st[x] = 0;
第六题 :奇怪的电梯
题目分析
dfs模板题 (指数枚举型模板1)
思路:依次枚举每层楼是上还是下
优化方案:没层楼最多走一次的方案比某层楼走过两次以上的方案要好(用到了全排列的思想)+剪枝
题目代码
import javax.print.DocFlavor; import java.util.Scanner; public class 奇怪的电梯_dfs static int n, A, B; static int k[]; static Boolean st[];//存每层罗走没走过 static int res = 10000; public static void main(String[] args) k = new int[250]; st = new Boolean[250]; Scanner sca = new Scanner(System.in); n = sca.nextInt(); A = sca.nextInt(); B = sca.nextInt(); for (int i = 1; i <= n; i++) k[i] = sca.nextInt(); st[i] = false; dfs(A, 0); if (res == 10000) System.out.println(-1); else System.out.println(res); //注意点:每当一次搜索,count按电梯数是叠加的,所以返回条件要注意什么时候才返回到上一次搜索 static void dfs(int x, int count) if (count >= res) return;//剪枝 if (x > n || x < 0) return; if (x == B) res = Math.min(res, count); return; if (x + k[x] <= n && !st[x + k[x]]) st[x + k[x]] = true; dfs(x + k[x], ++count);//上 st[x + k[x]] = false;//恢复现场 if (x - k[x] > 0 && !st[x - k[x]]) st[x - k[x]] = true; dfs(x - k[x], ++count);//下 st[x - k[x]] = false;有3个测试点没过
蓝桥杯DFS深度优先练习题——基础入门模板
目录
一个系列的文章——传送门
【蓝桥杯】DFS深度优先搜索练习题——提高篇(3)_小卢先冲的博客-CSDN博客第一题:入门迷宫问题、第二题:[USACO10OCT]Lake Counting S洪水灌溉问题、第三题:棋盘问题、第四题:[NOIP2001 提高组] 数的划分
https://blog.csdn.net/weixin_61082895/article/details/129912846?spm=1001.2014.3001.5501
【蓝桥杯】DFS深度优先练习题——基础入门(2)_小卢先冲的博客-CSDN博客第一题:[NOIP2002 普及组] 选数 、第二题:烤鸡 、 第三题:[NOIP2004 普及组] 火星人第四题:[NOIP2008 提高组] 火柴棒等式、第五题:PERKET、第六题:奇怪的电梯
https://blog.csdn.net/weixin_61082895/article/details/129895135?spm=1001.2014.3001.5501
第一题:递归实现指数型枚举
题目描述
从 1∼n 这 n 个整数中随机选取任意多个,输出所有可能的选择方案。
输入格式
输入一个整数 n。
输出格式
每行输出一种方案。
同一行内的数必须升序排列,相邻两个数用恰好 11 个空格隔开。
对于没有选任何数的方案,输出空行。
本题有自定义校验器(SPJ),各行(不同方案)之间的顺序任意。
数据范围
1≤n≤151≤n≤15
输入样例:
3输出样例:
3 2 2 3 1 1 3 1 2 1 2 3
模板一:递归实现指数型枚举
题目分析
n个数,每一个数都有俩种可能(选和不选)
可采用dfs对所有的可能进行搜索
题目代码
import java.util.Scanner; public class Main static int n; static int N = 20; static int st[]; //记录每一个数的状态,0表示还没考虑,1表示选这个数,2表示不选这个数。 public static void main(String[] args) st = new int[N]; Scanner sca = new Scanner(System.in); n = sca.nextInt(); dfs(1); static void dfs(int x) //x表示当前枚举到了哪个位置 if (x > 3) //结束这一次的循环,并且输出 for (int i = 1; i <= n; i++) if (st[i] == 1) System.out.print(i + " "); System.out.println(); return; //选 st[x] = 1; dfs(x + 1);//下一个位置 st[x] = 0;//每当上一个数的循环结束,都要恢复现场,因为每个数都有俩种选择选和不选 //不选 st[x] = 2; dfs(x + 1); st[x] = 0;//恢复现场
第二题:全排列问题
题目描述
按照字典序输出自然数 1 到 n 所有不重复的排列,即 n 的全排列,要求所产生的任一数字序列中不允许出现重复的数字。
输入格式
一个整数 n。
输出格式
由 1∼n 组成的所有不重复的数字序列,每行一个序列。
每个数字保留 5 个场宽。
输入输出样例
输入
3
输出1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1说明/提示
1≤n≤9。
模板二:全排列问题
题目分析
依次枚举每个位置放哪个数
题目代码
import java.util.Scanner; public class 全排列问题 static int N = 10; static int n; static Boolean st[];//false表示没有选这个数,true表示选了这个数 static int arr[];//用来存答案。也就是123/132/321 public static void main(String[] args) st = new Boolean[N]; for (int i = 0; i < st.length; i++) //初始化st为false,都没选 st[i] = false; arr = new int[N]; Scanner sca = new Scanner(System.in); n = sca.nextInt(); dfs(1); static void dfs(int x) //x表示当前枚举到了哪个位置 if (x > n) for (int i = 1; i <= n; i++) System.out.printf("%5d",arr[i]); System.out.println(); return; for (int i = 1; i <= n; i++) if (!st[i]) st[i] = true; arr[x] = i; dfs(x + 1);//下一个位置 st[i] = false;//恢复现场 arr[x] = 0;
第三题:组合的输出
题目描述
排列与组合是常用的数学方法,其中组合就是从 n 个元素中抽出 r 个元素(不分顺序且 r≤n),我们可以简单地将 n 个元素理解为自然数 1,2,…,n,从中任取 rr 个数。
现要求你输出所有组合。
例如 n=5,r=3,所有组合为:
123,124,125,134,135,145,234,235,245,345
输入格式
一行两个自然数 (1<n<21,0≤r≤n)。
输出格式
所有的组合,每一个组合占一行且其中的元素按由小到大的顺序排列,每个元素占三个字符的位置,所有的组合也按字典顺序。
注意哦!输出时,每个数字需要 33 个场宽。以 C++ 为例,你可以使用下列代码:
cout << setw(3) << x;输出占 33 个场宽的数 xx。注意你需要头文件
iomanip。输入输出样例
输入
5 3输出
1 2 3 1 2 4 1 2 5 1 3 4 1 3 5 1 4 5 2 3 4 2 3 5 2 4 5 3 4 5
模板三:组合型问题
题目分析
依次枚举每个位置放哪个数
题目代码
import javax.xml.stream.FactoryConfigurationError; import java.util.Scanner; public class 组合的输出 static int n, r; static int arr[];//记录都选了那些数 public static void main(String[] args) arr = new int[25]; Scanner sca = new Scanner(System.in); n = sca.nextInt(); r = sca.nextInt(); dfs(1, 1); //x记录当前枚举到了哪个位置,start记录当前位置从几开始枚举 static void dfs(int x, int start) if (x > r) for (int i = 1; i <= r; i++) System.out.printf("%3d", arr[i]); System.out.println(); return; for (int i = start; i <= n; i++) arr[x] = i; dfs(x + 1, i+ 1); arr[x] = 0;//恢复现场
以上是关于蓝桥杯DFS正确入门方式 | DFS + 递归与递推习题课(上) | 一节课教你爆搜!——学习笔记的主要内容,如果未能解决你的问题,请参考以下文章