算法模板：基础算法做题积累

Posted 2023-04-04 zhezhidashi

算法模板（1）：基础算法（3）做题积累

一、C++语法问题

编译优化

• 开启 O1 优化：#pragma GCC optimize(1)

• 开启 O2 优化：#pragma GCC optimize(2)

• 开启 O3 优化：#pragma GCC optimize(3)

stringstream && getline

• 用的时候带上"``iostream", "sstream", "string`"三个头文件。
• getline(cin, line)。其中line是一个string类对象。geiline结束读入标志是回车。但是一开始就遇到换行符的话还是会读入。
• stringstream ss(line)，其中line是一个string类对象。
• int x; while(ss >> x)，这样来把line中的数字挨个读入到 int 型变量里面。

二进制转化为格雷码方法：

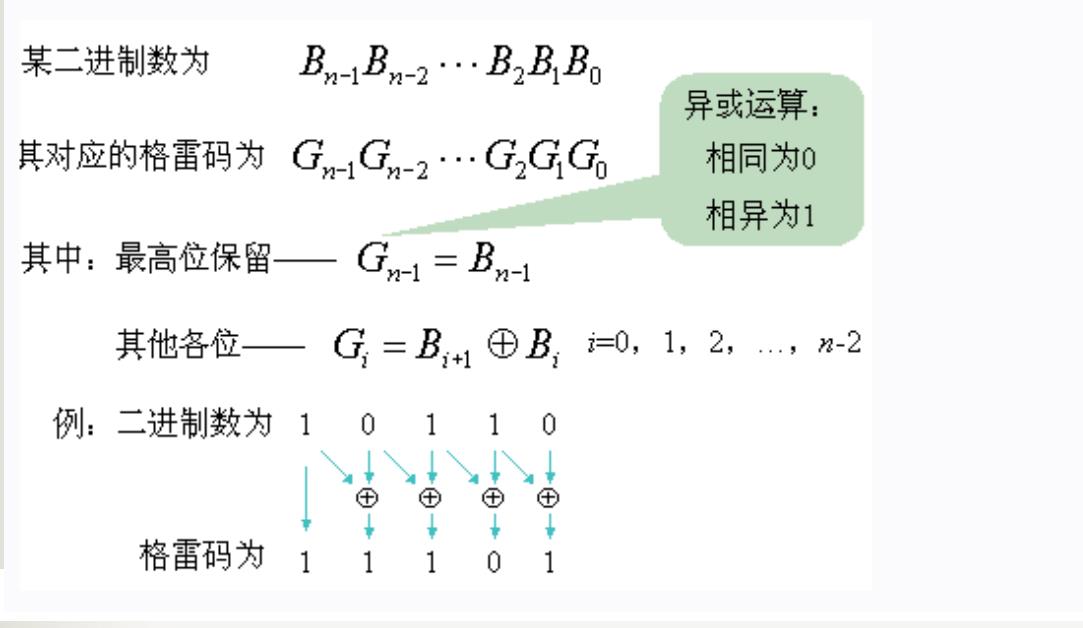
unordered_map 键用 pair 类型。

struct pair_hash

    template<class T1, class T2>
    std::size_t operator() (const std::pair<T1, T2>& p) const
    
        auto h1 = std::hash<T1>(p.first);
        auto h2 = std::hash<T2>(p.second);
        return h1 ^ h2;
    
;
unordered_map<pair<int, bool>, int, pair_hash> Map;

lower_bound && upper_bound

• lower_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

• upper_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

提高 cin, cout 速度

ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);

大质数

• 二进制下57位大质数：4179 34045 41998 20289LL

//求 x * y % mod, ll是long long, llf 是 long double
ll mul(ll x, ll y)

    ll tmp = x * y - ll(llf(x) * llf(y) / llf(mod)) * mod;
    return tmp < 0 ? tmp + mod : (tmp < mod ? tmp : tmp - mod);

随机数

mt19937 rnd(0);
int x = rnd();

二、排序

1. 122. 糖果传递

• 环形均分纸牌问题

• 有 $n$ 个小朋友坐成一圈，每人有 $a[i]$ 个糖果。每人只能给左右两人传递糖果。

  每人每次传递一个糖果代价为 1。

  求使所有人获得均等糖果的最小代价。

• 设第 $i$ 个人给第 $i-1$ 个人的糖果数为 $X_i$, 设所有人糖果的平均数是 $A$，那么第 i 个人的糖果数量是 $a_i-X_i+X_{i+1}$.

• 记 $f$ 为 $a$ 的前缀和，记 $c[i]$ 为 $f[i-1]-(i-1)\ast a$，mid 为 c 的中位数

对于第1个小朋友，A1-X1+X2=ave -> X2=ave-A1+X1 = X1-C1 (假设C1=A1-ave，下面类似）
对于第2个小朋友，A2-X2+X3=ave -> X3=ave-A2+X2=2ave-A1-A2+X1=X1-C2 即 C2=A1+A2-2ave=A2+C1-ave 以此类推
对于第3个小朋友，A3-X3+X4=ave -> X4=ave-A3+X3=3ave-A1-A2-A3+X1=X1-C3
我们的Ci的通式为 Ci=Ai+C[i-1]-ave!!!
……
对于第n个小朋友，An-Xn+X1=ave。
我们希望Xi的绝对值之和尽量小，即|X1| + |X1-C1| + |X1-C2| + ……+ |X1-Cn-1|要尽量小。注意到|X1-Ci|的几何意义是数轴上的点X1到Ci的距离

• 其实就是列几个方程就推出来了，在纸上写一写就出来了

• 答案就是 $|c_1-mid|+|c_2-mid|+...+|c_n-mid|.$

int main() 
	int N;
	scanf("%d", &N);
	for (int i = 1; i <= N; i++) 
		scanf("%lld", &a[i]);
		a[i] += a[i - 1];
	
	ll A = a[N] / N;
	for (int i = 1; i <= N; i++) 
		c[i] = a[i - 1] - (i - 1) * A;
	
	ll ans = 0;
	sort(c + 1, c + N + 1);
	ll mid = c[(N + 1) / 2];
	for (int i = 1; i <= N; i++) 
		ans += abs(c[i] - mid);
	
	printf("%lld\\n", ans);
	return 0;

2. 105. 七夕祭

• 一个 $N\ast M$ 的方格，其中若干方格点上面放了一个糖果。让每一行和每一列的糖果数量相等，求最小操作数。一次操作就是把相邻的两个元素交换，并且每行每列都可以看作一个环，就是第一个元素和最后一个元素相连。就转化为二维的环形均分纸牌问题。

首先输出一个字符串。

如果能满足 Vani 的全部两个要求，输出 both；

如果通过调整只能使得各行中 cl 感兴趣的摊点数一样多，输出 row；

如果只能使各列中 cl 感兴趣的摊点数一样多，输出 column；

如果均不能满足，输出 impossible。

如果输出的字符串不是 impossible， 接下来输出最小交换次数，与字符串之间用一个空格隔开。

• 行和列是独立的. 因为对行操作影响的是列, 对列操作影响的是行. 因此我们只需要求一下每行每列的和，这样就完全转化为一维的环形均分纸牌问题.

3. 106. 动态中位数

• 这道题也可以用平衡树来做，不过用堆更简单。
• 我们只关注中位数是多少，而前后是不用排序的。 所以，可以用一个小根堆和一个大根堆维护。
• 需要满足两个性质：小根堆的所有元素大于等于大根堆所有元素；大根堆的元素个数至多比小根堆多一个。那么，中位数就是大根堆堆顶元素。
• 第一个性质很好满足，对于一个新来的数x，如果大于小根堆堆顶元素，就放到小根堆里面，否则放到大根堆里面。
• 一定要万分小心，que.size() 返回值是size_t，而无符号整数与有符号整数直接判断的话，会强制转化为无符号整数，因此会出现 -2 > 1 的情况。

三、二分

102. 最佳牛围栏

• 题意：把选出一个连续子序列，该子序列至少有 $F$ 元素. 问每个子序列的平均值可能的最大值是多少 $(n\le 10^5).$

• 思路很简单，就是二分出答案。然后我们根据当前二分，把所有的数字都减去这个二分的结果。这样我们的目标就是找到一个连续子序列，使得平均值不小于0. 不需要写二重循环，打一个前缀和。固定右端点 $r$，寻找左端点 $l$，其实就是找到 1 ~ $l$ 的前缀和最小值 $minv$，则固定右端点为 $r$ 时能取到的最大值为 $s[r]-minv$.

• ans 在 $[l,r]$ 范围里，$l<=ans<=r$，因为向下取整，所以应该取输出时应取r.

• 这道题循环次数过多的话会出现精度问题，感觉不太对劲儿.

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 100010;
double a[maxn], s[maxn];
int N, F;
bool C(double x) 
	for (int i = 1; i <= N; i++) s[i] = a[i] - x + s[i - 1];
	double mins = 0, res = -1e9;
	for (int i = F; i <= N; i++) 
		mins = min(mins, s[i - F]);
		res = max(res, s[i] - mins);
	
	return res >= 0;

int main() 
	scanf("%d%d", &N, &F);
	for (int i = 1; i <= N; i++) scanf("%lf", &a[i]);
	double lb = 0, ub = 2000;
	while(ub - lb > 1e-5) 
		double mid = (lb + ub) / 2;
		if (C(mid)) lb = mid;
		else ub = mid;
	
	int ans = (int)(ub * 1000);
	printf("%d\\n", ans);
	return 0;

113. 特殊排序

• 看一看交互题是怎么写的. 给 $n$ 个点的图，有 $\frac{n(n-1)}{2}$ 条有向边，求一种排序方案. 该关系满足自反性，但不满足传递性.
• 二分找到一个 $res[l]\le i\le res[r]$ 的位置. 然后把 $i$ 插入 $res[l]$ 和 $res[r]$ 之间.

// Forward declaration of compare API.
// bool compare(int a, int b);
// return bool means whether a is less than b.

class Solution 
public:
    vector<int> specialSort(int N) 
        vector<int> res;
        res.push_back(1);
        for(int i = 2; i <= N; i++)
            int l = 0, r = res.size();
            while(r - l > 1)
                int mid = (l + r) / 2;
                if(compare(res[mid], i)) l = mid;
                else r = mid;
            
            res.push_back(i);
            for(int j = res.size() - 2; j >= r; j--) swap(res[j], res[j + 1]);
            //下面这个情况只可能是 l = 0 时. 否则一定会有一个 res[mid] < i 的情况使得 l = mid。
            if(compare(i, res[l])) swap(res[l], res[l + 1]);
        
        return res;
    
;

四、差分

100. 增减序列

• 题意：给定一个长度为 n 的数列 $a_1,a_2,\dots ,a_n$，每次可以选择一个区间 $[l,r]$，使下标在这个区间内的数都加 1 或者都减 1 . 求至少需要多少次操作才能使数列中的所有数都一样，以及得到数组的种类数量。
• 你会发现，求出来差分数组b，让第二项及以后数字全变成0。这样，整个数组的值只和第一项有关系。
• 而改变b中间两项的值，算作一次操作。因此求出b的正数和p以及负数和的绝对值q，操作数就是 m i n (

  《寒假算法集训》（专题十）前缀和

  文章目录

  • 一、算法概述
  • 二、博客教程
  • 三、视频教程
  • 四、模板地址
  • 五、必做题集
  • 六、选做题集

  一、算法概述

    「 前缀和 」 一般配合 「 差分算法 」，同时衍生出来的还有 「 前缀积 」、 「 前缀异或和 」 等等。
    以下博客教程，在寒假集训过程中均会 开启试读模式，无需购买 。

  二、博客教程

  以上是关于算法模板：基础算法做题积累的主要内容，如果未能解决你的问题，请参考以下文章

  《寒假算法集训》（专题十八）字典树

  《寒假算法集训》（专题十九）广度优先搜索

  《寒假算法集训》（专题十五）二叉树

  公钥、私钥、哈希、加密算法基础概念

  基础普及（15）：一分钟搞懂哈希以及哈希算法！

  模板 - 算法基础 - 输入输出