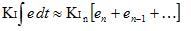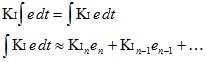Arduino PID库简介

Posted 2023-04-04 蔚蓝慕

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Arduino PID库简介相关的知识，希望对你有一定的参考价值。

Arduino PID库 – 简介

时间久远，可以参考
原文地址

随着新的Arduino PID库的发布，我决定发布这一系列的文章。最后一个库虽然很可靠，但并没有真正附带任何代码解释。这一次的计划是详细解释为什么代码是这样的。我希望这对两种人有用：

对Arduino PID库内部发生的事情直接感兴趣的人将获得详细的解释。
任何编写自己的PID算法的人都可以看看我是如何做事的，并借用他们喜欢的任何东西。

这将是一个艰难的过程，但我想我找到了一种不太痛苦的方式来解释我的代码。我将从我所谓的“初学者的PID”开始。然后，我将逐步改进它，直到我们得到一个高效、健壮的 pid 算法。

初学者的PID

这是每个人第一次学习的PID方程：

这导致几乎每个人都编写以下PID控制器：

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastErr;
double kp, ki, kd;
void Compute()

   /*How long since we last calculated*/
   unsigned long now = millis();
   double timeChange = (double)(now - lastTime);
  
   /*Compute all the working error variables*/
   double error = Setpoint - Input;
   errSum += (error * timeChange);
   double dErr = (error - lastErr) / timeChange;
  
   /*Compute PID Output*/
   Output = kp * error + ki * errSum + kd * dErr;
  
   /*Remember some variables for next time*/
   lastErr = error;
   lastTime = now;

  
void SetTunings(double Kp, double Ki, double Kd)

   kp = Kp;
   ki = Ki;
   kd = Kd;

Compute（）被定期或不定期调用，它运行良好。不过，这个系列并不是关于“效果很好”。如果我们要把这段代码变成与工业PID控制器相提并论的东西，我们必须解决一些问题：

**sample time采样时间 –**PID 算法如果定期评估，则功能最佳。如果算法知道这个区间，我们还可以简化一些内部数学。
**Derivative Kick –**这不是最大的问题，很容易摆脱，所以我们要这样做。
**On-The-Fly Tuning Changes即时调谐更改 –**一个好的PID算法是可以在不干扰内部工作的情况下更改调谐参数的算法。
**Reset Windup Mitigation重置清盘缓解 –**我们将介绍什么是重置清盘，并实施具有副作用的解决方案
**on/off(Auto/Manual开/关（自动/手动）–**在大多数应用中，有时希望关闭PID控制器并手动调整输出，而不会干扰控制器
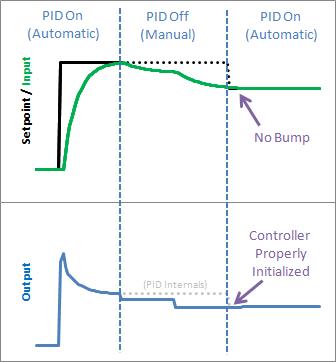
**Initialization初始化–**当控制器首次打开时，我们想要“无颠簸传输”。也就是说，我们不希望输出突然猛地跳动到某个新值。
**Controller Direction控制器方向 –**最后一个并不是健壮性名称本身的更改。它旨在确保用户输入具有正确符号的优化参数。
**NEW: Proportional on Measurement新：测量比例 –**添加此功能可以更轻松地控制某些类型的进程

一旦我们解决了所有这些问题，我们将拥有一个可靠的PID算法。我们还将拥有在最新版本的Arduino PID库中使用的代码。因此，无论您是尝试编写自己的算法，还是尝试了解PID库中发生的事情，我都希望对您有所帮助。让我们开始吧。
下一>>

更新：在所有代码示例中，我都使用双精度。在Arduino上，双精度与浮点数相同（单精度）。真正的双精度对于PID来说是矫枉过正的。如果您使用的语言确实是双精度，我建议将所有双精度更改为浮点数。

提高初学者的 PID – 采样时间

（这是关于编写固定 PID 算法的更大系列中的修改 #1）

问题所在

初学者的PID被设计为不规则地调用。这会导致 2 个问题：

您不会从 PID 获得一致的行为，因为有时它经常被调用，有时则不然。
你需要做额外的数学计算导数和积分，因为它们都依赖于时间的变化。

解决方案

确保定期调用 PID。我决定这样做的方法是指定每个周期调用计算函数。根据预先确定的采样时间，PID 决定是否应立即计算或返回。

一旦我们知道PID正在以恒定的间隔进行评估，也可以简化导数和积分计算。

《代码》

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastErr;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
void Compute()

   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      errSum += error;
      double dErr = (error - lastErr);
 
      /*Compute PID Output*/
      Output = kp * error + ki * errSum + kd * dErr;
 
      /*Remember some variables for next time*/
      lastErr = error;
      lastTime = now;
   

 
void SetTunings(double Kp, double Ki, double Kd)

  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;

 
void SetSampleTime(int NewSampleTime)

   if (NewSampleTime > 0)
   
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;

在第 10 行和第 11 行，算法现在自行决定是否需要计算。此外，因为我们现在知道样本之间的时间是相同的，所以我们不需要不断地乘以时间变化。我们只能适当地调整 Ki 和 Kd（第 31 和 32 行），结果在数学上是等价的，但效率更高。

不过，这样做有点问题。如果用户决定在操作过程中更改采样时间，则需要重新调整Ki和Kd以反映此新更改。这就是第 39-42 行的全部内容。

另请注意，我将第 29 行的采样时间转换为秒。严格来说，这不是必需的，但允许用户以 1/秒为单位输入 Ki 和 Kd，而不是 1/mS。

结果

上述更改为我们做了 3 件事

无论调用 Compute（）的频率如何，PID 算法都将定期评估 [第 11 行]
由于时间减法 [第 10 行]，当 millis（）返回 0 时不会有问题。这每 55 天才会发生一次，但我们要防止还记得吗？
我们不再需要乘以时间变化。由于它是一个常量，我们可以将其从计算代码 [第 15+16 行] 中移出，并将其与调优常量 [第 31+32 行] 混为一谈。从数学上讲，它的工作原理相同，但是每次计算PID时都会节省乘法和除法

关于中断的旁注

如果这个PID进入微控制器，则可以为使用中断提出一个很好的论据。SetSampleTime 设置中断频率，然后在需要时调用 Compute。在这种情况下，不需要第 9-12、23 和 24 行。如果您打算用PID影响来做到这一点，那就去做吧！不过，请继续阅读本系列。希望您仍然可以从随后的修改中获得一些好处。
我没有使用中断有三个原因

就本系列而言，并不是每个人都能使用中断。
如果您希望它同时实现许多PID控制器，事情会变得棘手。
老实说，我没有想到。吉米·罗杰斯（Jimmie Rodgers）在为我校对该系列时提出了这个建议。我可能决定在PID库的未来版本中使用中断。

提高初学者的 PID – Derivative Kick

（这是关于编写可靠 PID 算法的更大系列中的修改 #2）

问题所在

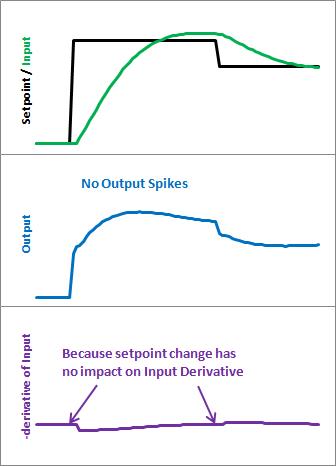
此修改将稍微调整derivative term。目标是消除一种称为“Derivative Kick”的现象。

上图说明了问题。由于error=Setpoint-Input，因此Setpoint的任何更改都会导致误差的瞬时变化。这种变化的导数是无穷大（在实践中，由于 dt 不是 0，它最终只是一个非常大的数字。该数字被馈入pid方程，从而导致输出中出现不希望的尖峰。幸运的是，有一种简单的方法可以摆脱这种情况。

解决方案

事实证明，误差的导数等于输入的负导数，除非设定值发生变化。这最终是一个完美的解决方案。我们不是加（Kd * 误差的导数），而是减去（输入的 Kd * 导数）。这称为使用“测量导数”

《代码》

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
void Compute()

   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      errSum += error;
      double dInput = (Input - lastInput);
 
      /*Compute PID Output*/
      Output = kp * error + ki * errSum - kd * dInput;
 
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   

 
void SetTunings(double Kp, double Ki, double Kd)

  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;

 
void SetSampleTime(int NewSampleTime)

   if (NewSampleTime > 0)
   
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;

这里的修改非常简单。我们将 +dError 替换为 -dInput。我们现在不再记住最后一个错误，而是记住最后一个输入

结果

以下是这些修改给我们带来的结果。请注意，输入看起来仍然大致相同。因此，我们获得了相同的性能，但我们不会在每次设定值更改时都发出巨大的输出峰值。

这可能是也可能不是什么大问题。这完全取决于您的应用程序对输出峰值的敏感程度。不过，在我看来，不突变就不需要做更多的工作，所以为什么不把事情做好呢？
下一>>

改进初学者的 PID：调整更改

（这是关于编写固体 PID 算法的更大系列中的修改 #3）

问题所在

在系统运行时更改调谐参数的能力对于任何PID算法都是必须的。

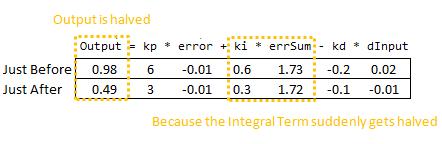
初学者的PID在运行时尝试整定，表现得有点疯狂。让我们看看为什么。以下是上述参数更改前后初学者的PID状态：

因此，我们可以立即将这种颠簸归咎于积分项（或“I 项”）。这是参数更改时唯一发生巨大变化的东西。为什么会这样？这与初学者对积分的解释有关：

在 Ki 更改之前，这种解释效果很好。然后，突然之间，您将这个新 Ki 乘以您累积的整个误差总和。那不是我们想要的！我们只想影响事情的发展！

解决方案

我知道有几种方法可以解决这个问题。我在上一个库中使用的方法是重新缩放 errSum。Ki加倍了？将errSum减半。这样可以防止 I 项发生碰撞，并且它有效。不过有点笨拙，我想出了更优雅的东西。（我不可能是第一个想到这一点的人，但我确实自己想到了。

解决方案需要一点基本的代数（或者是微积分？

我们不是让 Ki 生活在积分之外，而是把它带入内部。看起来我们什么都没做，但我们会看到在实践中这有很大的不同。

现在，我们取error并将其乘以当时的 Ki。然后我们存储 THAT 的总和。当 Ki 发生变化时，不会有颠簸，因为可以这么说，所有旧的 Ki 都已经“在银行里”。我们无需额外的数学运算即可顺利转移。

《代码》

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
void Compute()

   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      ITerm += (ki * error);
      double dInput = (Input - lastInput);
 
      /*Compute PID Output*/
      Output = kp * error + ITerm - kd * dInput;
 
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   

 
void SetTunings(double Kp, double Ki, double Kd)

  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;

 
void SetSampleTime(int NewSampleTime)

   if (NewSampleTime > 0)
   
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;

因此，我们将 errSum 变量替换为复合 ITerm 变量 [第 4 行]。它对 Ki*error 求和，而不仅仅是error [第 15 行]。此外，由于 Ki 现在包含在 ITerm 中，因此它已从主 PID 计算 [第 19 行] 中删除。

结果

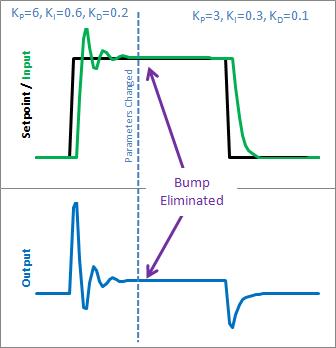
那么这如何解决问题。在更改 ki 之前，它会重新缩放整个error的总和;我们看到的每一个error值。使用此代码，以前的错误保持不变，新的 ki 只会影响将来的事情，这正是我们想要的。

改善初学者的 PID：Reset Windup

（这是关于编写可靠PID算法的更大系列中的修改#4）

问题所在

Reset Windup是一个陷阱，可能比其他任何陷阱都需要更多的初学者。当 PID 认为它可以做一些它不能做的事情时，就会发生这种情况。例如，Arduino上的PWM输出接受0-255之间的值。默认情况下，PID 不知道这一点。如果它认为 300-400-500 会起作用，它会尝试这些值，期望得到它需要的东西。由于实际上该值被固定在 255，因此它只会继续尝试越来越高的数字而无处可去。

问题以奇怪的滞后形式显现出来。上面我们可以看到输出“卷绕”在外部限制以上。当设定值下降时，输出必须在低于255线之前逐渐减少。

解决方案 – 步骤 1

有几种方法可以减轻windup，但我选择的方法如下：告诉PID输出限制是什么。在下面的代码中，您将看到现在有一个 SetOuputLimits 函数。一旦达到任一限制，pid 将停止求和（积分）。它知道没有什么可做的;由于输出不会结束，因此当Setpoint下降到我们可以做某事的范围内时，我们会立即得到响应。

解决方案 – 步骤 2

请注意，在上图中，虽然我们摆脱了windup滞后，但我们并没有一路走来。pid 认为它正在发送的内容和正在发送的内容之间仍然存在差异。为什么？比例项和（在较小程度上）微分项。

即使积分项已被安全控制，P和D仍然加两点，产生高于输出限值的结果。在我看来，这是不可接受的。如果用户调用一个名为“SetOutputLimits”的函数，他们必须假设这意味着“输出将保持在这些值内”。因此，对于第 2 步，我们将其作为有效的假设。除了限制 I 项外，我们还限定输出值，使其保持在我们预期的位置。

（注意：你可能会问为什么我们需要同时限定两者。如果我们无论如何都要做输出，为什么要单独限定积分？如果我们所做的只是限定输出，积分项将逐步增长。虽然输出在升压期间看起来不错，但我们会看到降阶时明显滞后。

《代码》

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
void Compute()

   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      ITerm += (ki * error);
      if(ITerm> outMax) ITerm= outMax;
      else if(ITerm< outMin) ITerm= outMin;
      double dInput = (Input - lastInput);

      /*Compute PID Output*/
      Output = kp * error + ITerm- kd * dInput;
      if(Output > outMax) Output = outMax;
      else if(Output < outMin) Output = outMin;

      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   


void SetTunings(double Kp, double Ki, double Kd)

  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;


void SetSampleTime(int NewSampleTime)

   if (NewSampleTime > 0)
   
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   


void SetOutputLimits(double Min, double Max)

   if(Min > Max) return;
   outMin = Min;
   outMax = Max;
   
   if(Output > outMax) Output = outMax;
   else if(Output < outMin) Output = outMin;

   if(ITerm> outMax) ITerm= outMax;
   else if(ITerm< outMin) ITerm= outMin;

添加了一个新函数，允许用户指定输出限制 [第 52-63 行]。这些限值用于限定I项[17-18]和输出[23-24]

结果

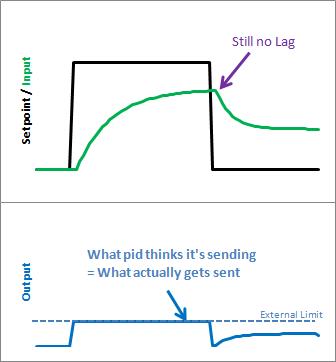
正如我们所看到的，windup被消除了。此外，输出保留在我们想要的位置。这意味着无需对输出进行外部限制。如果您希望它的范围从 23 到 167，则可以将其设置为输出限制。
下一>>

提高初学者的PID：开/关

（这是关于编写可靠PID算法的更大系列中的修改#5）

问题所在

尽管拥有一个PID控制器很好，但有时你并不关心它要说什么。

假设在程序中的某个时刻，您希望将输出强制为某个值（例如 0），您当然可以在调用例程中执行此操作：

void loop()

Compute();
Output=0;

这样，无论 PID 说什么，您都只需覆盖其值。然而，这在实践中是一个糟糕的想法。PID会变得非常困惑：“我一直在移动输出，什么也没发生！给什么？！让我再动一下。因此，当您停止覆盖输出并切换回 PID 时，您可能会立即获得输出值的巨大变化。

解决方案

这个问题的解决方案是有一种关闭和打开PID的方法。这些状态的常用术语是“手动”（我将手动调整值）和“自动”（PID 将自动调整输出）。让我们看看这是如何在代码中完成的：

《代码》

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
bool inAuto = false;
 
#define MANUAL 0
#define AUTOMATIC 1
 
void Compute()

   if(!inAuto) return;
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      ITerm+= (ki * error);
      if(ITerm> outMax) ITerm= outMax;
      else if(ITerm< outMin) ITerm= outMin;
      double dInput = (Input - lastInput);
 
      /*Compute PID Output*/
      Output = kp * error + ITerm- kd * dInput;
      if(Output > outMax) Output = outMax;
      else if(Output < outMin) Output = outMin;
 
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   

 
void SetTunings(double Kp, double Ki, double Kd)

  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;

 
void SetSampleTime(int NewSampleTime)

   if (NewSampleTime > 0)
   
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   

 
void SetOutputLimits(double Min, double Max)

   if(Min > Max) return;
   outMin = Min;
   outMax = Max;
    
   if(Output > outMax) Output = outMax;
   else if(Output < outMin) Output = outMin;
 
   if(ITerm> outMax) ITerm= outMax;
   else if(ITerm< outMin) ITerm= outMin;

 
void SetMode(int Mode)

  inAuto = (Mode == AUTOMATIC);

一个相当简单的解决方案。如果未处于自动模式，请立即离开计算函数，而不调整输出或任何内部变量。

结果

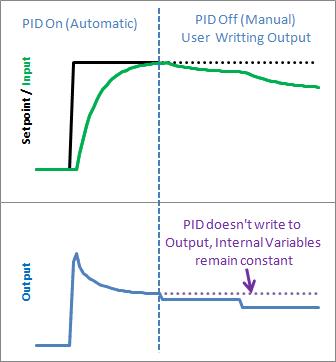
确实，您可以通过不从调用例程调用 Compute 来实现类似的效果，但此解决方案保留了 PID 的工作原理，这正是我们所需要的。通过将事情保持在内部，我们可以跟踪处于哪种模式，更重要的是，当我们更改模式时，它可以让我们知道。这就引出了下一个问题…
下一>>

改进初学者的 PID：初始化

（这是关于编写可靠PID算法的更大系列中的修改#6）

问题所在

在上一节中，我们实现了关闭和打开PID的功能。我们关闭了它，但现在让我们看看当我们重新打开它时会发生什么：

哎呀！PID 跳回到它发送的最后一个输出值，然后从那里开始调整。这会导致我们不希望有的输入凸起。

解决方案

这个很容易修复。由于我们现在知道何时打开（从手动到自动），我们只需要初始化即可平稳过渡。这意味着massaging2个存储的工作变量（ITerm和lastInput）以防止输出跳转。

《代码》

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
bool inAuto = false;
 
#define MANUAL 0
#define AUTOMATIC 1
 
void Compute()

   if(!inAuto) return;
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      ITerm+= (ki * error);
      if(ITerm> outMax) ITerm= outMax;
      else if(ITerm< outMin) ITerm= outMin;
      double dInput = (Input - lastInput);
 
      /*Compute PID Output*/
      Output = kp * error + ITerm- kd * dInput;
      if(Output> outMax) Output = outMax;
      else if(Output < outMin) Output = outMin;
 
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   

 
void SetTunings(double Kp, double Ki, double Kd)

  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;

 
void SetSampleTime(int NewSampleTime)

   if (NewSampleTime > 0)
   
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   

 
void SetOutputLimits(double Min, double Max)

   if(Min > Max) return;
   outMin = Min;
   outMax = Max;
    
   if(Output > outMax) Output = outMax;
   else if(Output < outMin) Output = outMin;
 
   if(ITerm> outMax) ITerm= outMax;
   else if(ITerm< outMin) ITerm= outMin;

 
void SetMode(int Mode)

    bool newAuto = (Mode == AUTOMATIC);
    if(newAuto && !inAuto)
      /*we just went from manual to auto*/
        Initialize();
    
    inAuto = newAuto;

 
void Initialize()

   lastInput = Input;
   ITerm = Output;
   if(ITerm> outMax) ITerm= outMax;
   else if(ITerm< outMin) ITerm= outMin;

我们修改了 SetMode（...） 以检测从手动到自动的转换，并添加了初始化函数。它设置 ITerm=Output 来处理积分项，lastInput = Input以防止导数出现峰值。比例项不依赖于过去的任何信息，因此不需要任何初始化。

结果

我们从上图中看到，正确的初始化会导致从手动到自动的无颠簸转移：这正是我们所追求的。
下一>>

更新：为什么不是 ITerm=0？

我最近收到很多问题，问为什么我不在初始化时设置 ITerm=0。作为答案，我要求您考虑以下场景：pid 是手动的，用户已将输出设置为 50。一段时间后，该过程稳定到输入 75.2。用户设定值为 75.2 并打开 pid。应该怎么做？

我认为切换到自动后，输出值应保持在 50。由于 P 和 D 项将为零，因此发生这种情况的唯一方法是将 ITerm 初始化为输出值。

如果您处于需要输出初始化为零的情况，则无需更改上面的代码。只需在调用例程中设置 Output=0，然后将 PID 从手动转换为自动。

提高初学者的PID：方向

（这是关于编写固体PID算法的更大系列中的最后一次修改）

问题所在

PID连接的过程分为两组：直接作用和反向作用。到目前为止，我展示的所有例子都是直接行动。也就是说，输出的增加会导致输入的增加。对于反向作用过程，情况正好相反。例如，在冰箱中，冷却的增加会导致温度下降。为了使初学者 PID 使用反向过程，kp、ki 和 kd 的符号都必须为负数。

这本身不是问题，但用户必须选择正确的符号，并确保所有参数都具有相同的符号。

解决方案

为了使过程更简单一些，我要求 kp、ki 和 kd 都>=0。如果用户连接到反向进程，则使用SetControllerDirection 函数单独指定。这确保了所有参数都具有相同的符号，并希望使事情更加直观。

《代码》

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
bool inAuto = false;
 
#define MANUAL 0
#define AUTOMATIC 1
 
#define DIRECT 0
#define REVERSE 1
int controllerDirection = DIRECT;
 
void Compute()

   if(!inAuto) return;
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      ITerm+= (ki * error);
      if(ITerm > outMax) ITerm= outMax;
      else if(ITerm < outMin) ITerm= outMin;
      double dInput = (Input - lastInput);
 
      /*Compute PID Output*/
      Output = kp * error + ITerm- kd * dInput;
      if(Output > outMax) Output = outMax;
      else if(Output < outMin) Output = outMin;
 
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   

 
void SetTunings(double Kp, double Ki, double Kd)

   if (Kp<0 || Ki<0|| Kd<0) return;
 
  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;
 
  if(controllerDirection ==REVERSE)
   
      kp = (0 - kp);
      ki = (0 - ki);
      kd = (0 - kd);
   

 
void SetSampleTime(int NewSampleTime)

   if (NewSampleTime > 0)
   
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   

 
void SetOutputLimits(double Min, double Max)

   if(Min > Max) return;
   outMin = Min;
   outMax = Max;
 
   if(Output > outMax) Output = outMax;
   else if(Output < outMin) Output = outMin;
 
   if(ITerm > outMax) ITerm= outMax;
   else if(ITerm < outMin) ITerm= outMin;

 
void SetMode(int Mode)

    bool newAuto = (Mode == AUTOMATIC);
    if(newAuto == !inAuto)
      /*we just went from manual to auto*/
        Initialize();
    
    inAuto = newAuto;

 
void Initialize()

   lastInput = Input;
   ITerm = Output;
   if(ITerm > outMax) ITerm= outMax;
   else if(ITerm < outMin) ITerm= outMin;

 
void SetControllerDirection(int Direction)

   controllerDirection = Direction;

PID 完成

这就结束了。我们已经把“初学者的PID”变成了我目前知道如何制作的最强大的控制器。对于那些正在寻找PID库详细解释的读者，我希望你得到你想要的。对于那些编写自己的PID的人，我希望你们能够收集一些想法，从而节省一些周期。

最后两点：

如果本系列中的某些内容看起来有问题，请告诉我。我可能错过了一些东西，或者可能只需要在我的解释中更清楚。无论哪种方式，我都想知道。
这只是一个基本的PID。为了简单起见，我故意省略了许多其他问题。我的头顶：前馈，重置回扣，整数数学，不同的pid形式，使用速度而不是位置。如果有兴趣让我探索这些主题，请告诉我。

嵌入式STM32利用arm-dsp库进行PID调节控制

在工程实际中，应用最为广泛的调节器控制规律为比例、积分、微分控制，简称 PID 控制，又称 PID调节。其原理介绍教科书以及网上已经有大量资料，本文着重介绍在嵌入式设备中，如何快速上手进行PID控制，并通过简单的单片机外设进行验证。

一、实验简介

1.原理

我们知道，可以通过调节PWM的占空比来起到调节等效电压的效果。比如U=D*Ud，其中U为输出的等效电压，D为占空比，Ud为单极性PWM的峰值电压，这常用在电机控制中。
当要维持输出电压U为某一确定值Us时，往往要形成回路以准确得控制U的大小，这就要用到ADC来回采电压Us，利用某种控制手段使得输出的电压U与确定值Us误差维持在一定范围内。其中，这种控制方法最为常用的就是PID控制。
以经典反馈控制回路为例：
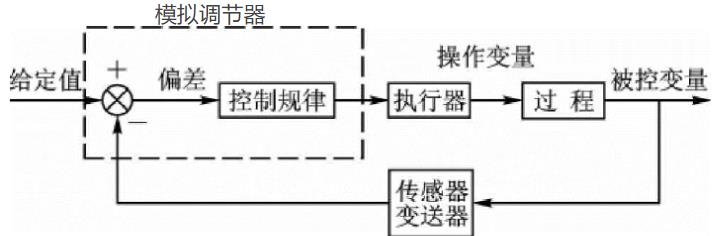
在这里插入图片描述
其中给定值即为Us；控制规律为PID；执行器即为占空比的调整；过程即为PWM输出；被控变量即为U；传感器即为ADC。本系统采用PID控制时，可作以下描述：PWM输出的电压值U被ADC采样后，回环送入调节器与给定值Us相比较，获得一个偏差送入PID调节器，通过PID来控制PWM占空比的大小从而起到调节电压U的效果，最终使得电压U与给定值Us之间的误差稳定在某个设定的范围阈值之内。

2.所用外设

我们利用一个单片机核心板即可进行上述的PID调节PWM的实验。
其中，PWM由定时器输出；通过片内ADC进行电压回采、处理；通过arm-dsp库进行PID调节。
综上，本实验用到以下外设：
1.定时器的PWM输出；
2.定时器触发的ADC采样；
3.ADC采样的DMA传输；

二、代码

依旧用到了STM32CubeMX来进行驱动代码的生成。
这里规定了几个重要的参数：
1.STM32F407，配置主频160MHz；
1.PWM载波50Hz；
2.ADC采样率4000Hz；

1.PWM输出配置

使用TIMER3来输出PWM，160MHz主频下，TIMER3的时钟为80MHz，将在这个基础上分频到50Hz；
首先配置TIM3的PWM输出通道：
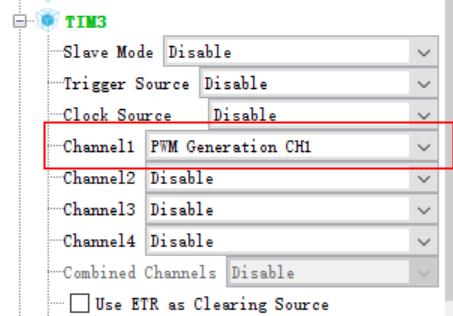
在这里插入图片描述
然后分频到50Hz，同时设置PWM极性高，Pulse随便设置即可，为了最大程度体现PID的效果，我们初始设置为0，在PWM极性高时，Pulse为0意味着PWM通道总是输出低，即PWM初始的等效电压为0.

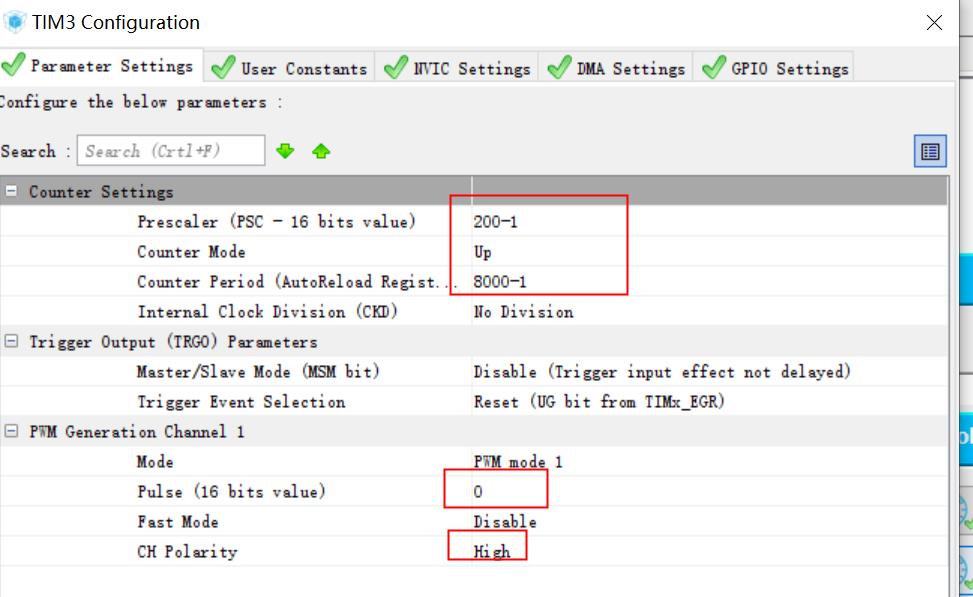
2.定时器触发的DMA传输的ADC

这个完全参考我之前的博客即可，【嵌入式】STM32F4的ADC采样——多通道、DMA、定时器触发，唯一的区别在于此处只用了一通道，更简单了。
生成代码后，硬件上将PWM通道直接怼到ADC1的0通道即可。

3.主体代码

#include "main.h"
#include "stm32f4xx_hal.h"
#include "adc.h"
#include "dma.h"
#include "tim.h"
#include "gpio.h"
#include "arm_math.h"
void SystemClock_Config(void);


#define BUF_LEN 			400			//采样数组长度
#define PWM_PERIOD_CCR1		8000		//PWM周期-计数值
#define DES_VOL				1.0			//目标电压
#define ERR_LIMIT			0.05		//误差限制


typedef struct{
    arm_pid_instance_f32  S;
    float                 out;
}PidCtrlTypedef;						//pidt调节结构体

volatile uint8_t dma_cpl_flag = 0;		//dma传输完成标志
uint16_t adc_raw[BUF_LEN] = {0};		//adc原始采样值
uint16_t adc_raw_copy[BUF_LEN] = {0};	//adc原始采样值备份
float cur_vol = 0;						//当前电压

PidCtrlTypedef pidCtrl;					//pid调节实例

/* ADC-DMA全传输完成回调 */
void HAL_ADC_ConvCpltCallback(ADC_HandleTypeDef *hadc)
{
	UNUSED(hadc);

	memcpy((void *)adc_raw_copy,(void *)adc_raw,sizeof(adc_raw));

	dma_cpl_flag = 1;
}

/* 根据原始采样值计算PWM等效电压值 */
float calVol()
{
	int i;
	float res;
	float sum = 0;
	float tempVal;
	for(i = 0;i < BUF_LEN; i++)
	{
		tempVal = adc_raw_copy[i] * 3.3 / 4095;
		sum += tempVal;
	}
	
	res = sum / BUF_LEN;

	cur_vol = res;

	return res;
} 

/* PID初始化 */
void pidInit()
{
    pidCtrl.S.Kp = 0.1;
    pidCtrl.S.Ki=0.1;
    pidCtrl.S.Kd = 0.1;
    arm_pid_init_f32(&pidCtrl.S,1);

    pidCtrl.out = 0;
}

/* PID执行 */
static void pidExecu(float vol)
{
    float pidErr;

    pidErr = DES_VOL - vol;	
	//误差不在允许范围内
	if(fabs(pidErr) > ERR_LIMIT)
    {
    	pidCtrl.out = arm_pid_f32(&pidCtrl.S,pidErr);
		//     vol			   pidCtrl.out
		//  ——————————   =    ————————————
		//	当前占空比			调节后占空比
		htim3.Instance->CCR1 = (uint32_t)(pidCtrl.out * (htim3.Instance->CCR1 + 1) / vol);
	}
}
/* USER CODE END 0 */

/**
  * @brief  The application entry point.
  *
  * @retval None
  */
int main(void)
{
	HAL_Init();

	SystemClock_Config();
	MX_GPIO_Init();
	MX_DMA_Init();
	MX_ADC1_Init();
	MX_TIM2_Init();
	MX_TIM3_Init();
	//pid初始化
	pidInit();
	//开启AD转换时钟
	HAL_TIM_Base_Start(&htim2);
	//开启PWM输出
	HAL_TIM_PWM_Start(&htim3, TIM_CHANNEL_1);
	//开启ADC-DMA传输
	HAL_ADC_Start_DMA(&hadc1, (uint32_t *)adc_raw, BUF_LEN);

	while (1)
	{
		if(dma_cpl_flag == 1)
		{
			dma_cpl_flag = 0;
			pidExecu(calVol());
		}
	}

}

以上代码即为主体逻辑代码。流程如下：
1.外设初始化；
2.PID初始化；
3.开启AD转换时钟；
4.开启PWM输出；
5.开启ADC-DMA采样；
6.每次DMA传输完成中断后，进行PWM有效值计算、PID控制、PWM占空比调节。
同时，程序中有几个关键点：
1.设置DMA的长度为400，即采样率4000Hz时、PWM载波50Hz时，采样100ms进一次DMA传输完成中断，共采了5周期的PWM，从而能直接对400个采样点取平均，得到PWM的有效值。即采样长度一定要为PWM载波的整数倍，且采样率要远大于PWM载波频率；
2.利用arm-dsp库进行PID控制要在工程中加入arm-dsp的lib库，具体方法请参考博客【嵌入式】利用arm-DSP库进行FFT计算，获得信号的频谱、幅值及相位(上)的二-1小节；
3.arm_pid_f32函数声明如下：

static __INLINE float32_t arm_pid_f32(
  arm_pid_instance_f32 * S,
  float32_t in)

其中S为arm_pid_instance_f32 实例指针，在arm_pid_init_f32函数中实例化。要注意的是变量in，这个in是给定值与反馈值的误差，其在arm_math.h中做了阐述：

The PID controller calculates an "error" value as the difference between
   * the measured output and the reference input.
   * The controller attempts to minimize the error by adjusting the process control inputs.
   * The proportional value determines the reaction to the current error,
   * the integral value determines the reaction based on the sum of recent errors,
   * and the derivative value determines the reaction based on the rate at which the error has been changing.

了解了这几点，再配合上边注释详细的程序，即可理解实验过程以及PID调节的使用方法。具体Kp、Ki、Kd参数的调节，还需要根据不同场景来进行耐心调节。

三、实验结果

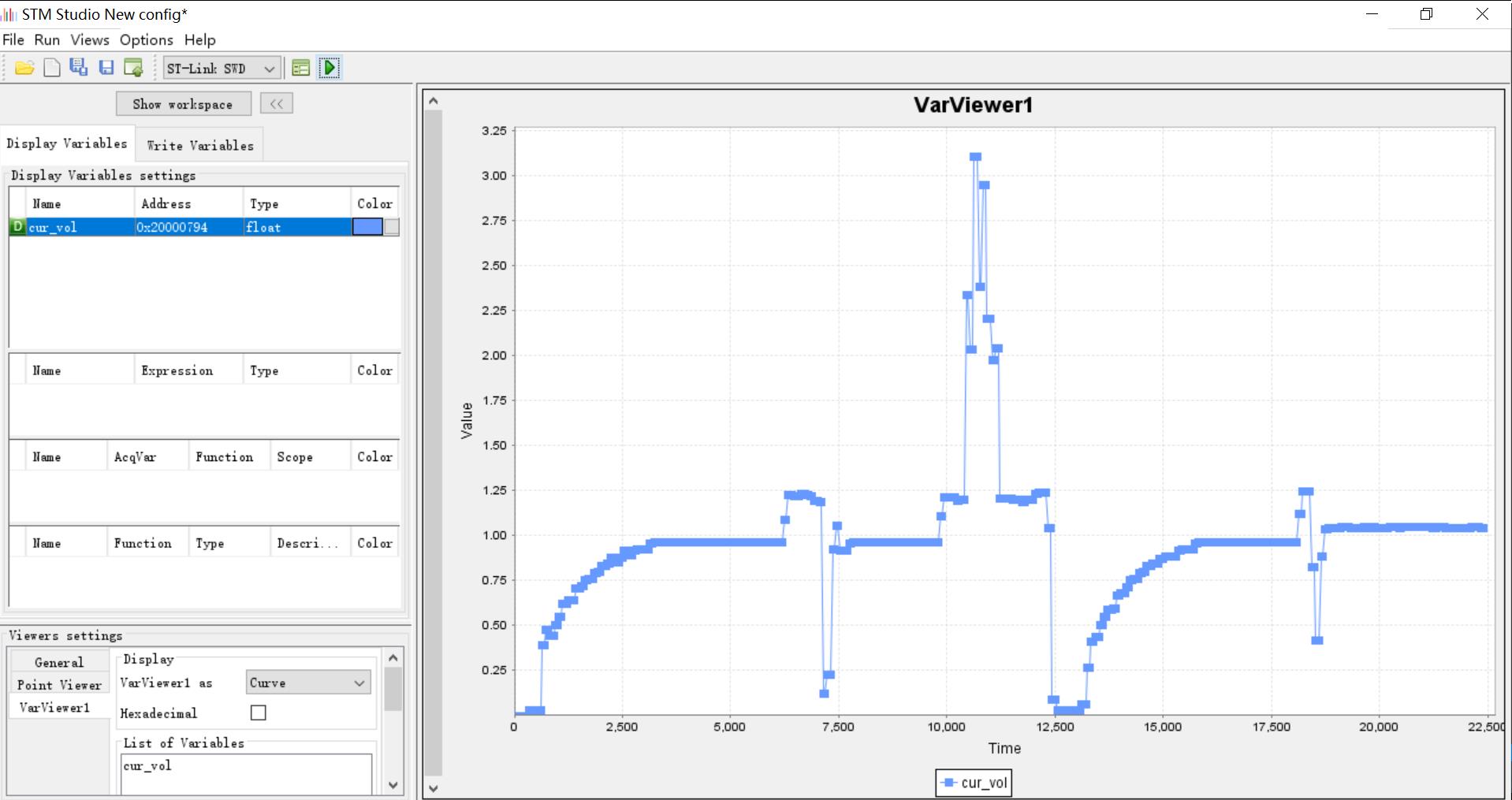
程序中定义了变量cur_vol以存储当前采到的PWM有效值，为了直观的体现PID对PWM的调节过程，使用STM32Studio进行变量实时调试，具体使用方法请自行百度。
可以看到，在设置期望值1V、初始PWM输出为0V、最大允许误差0.05V时，PID控制器可在2秒内平滑稳定得将输出值调节到误差0.05V之内。且人为地多次随机插拔采样通道使得采样值扰动、PWM失稳后，PID控制器总能再次平稳得将输出值再次调节到1V±0.05V之内。
这就体现了PID控制的实用价值所在，至于调节速度、震荡速度、允许误差等，可以通过实际工程需求进行整定、调整。
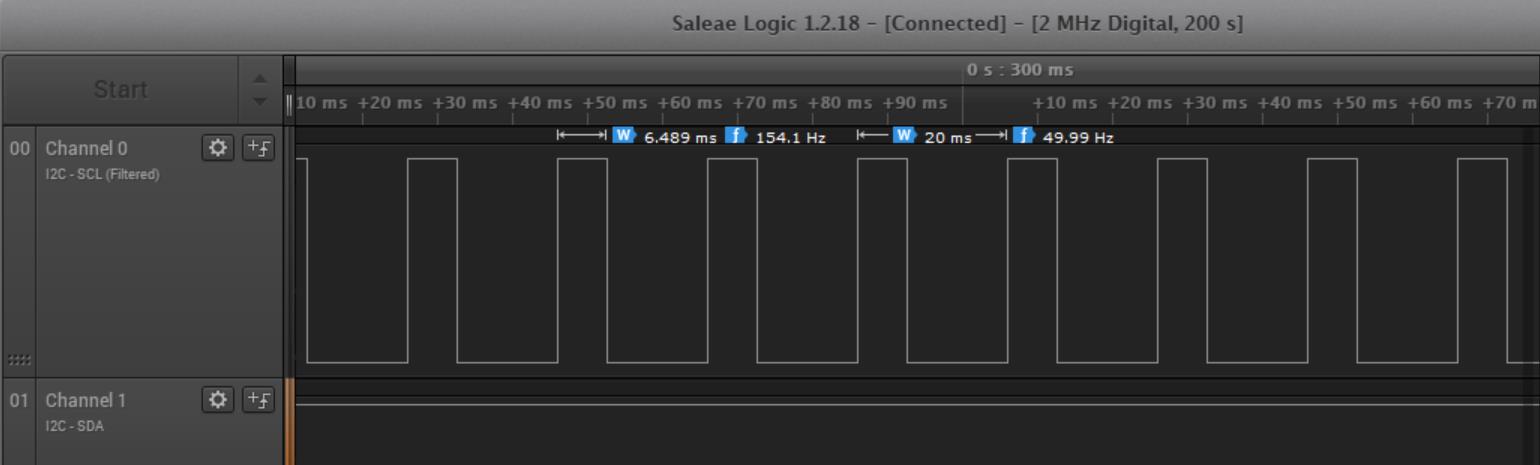
在这里插入图片描述
最后，贴一张调节稳定后的PWM实测波形，可以看到其占空比约为6.489/20 = 32.445%，以AD基准电压3.3V来算，其输出电压为3.3*0.32445 = 1.070685V，这个值由于逻辑分析仪的占空比采样误差、3.3V基准误差的存在，使得与1V有一定的偏差。同时程序里也规定了0.95~1.05V范围内是期望范围。
综上，PID调节起到了应有的作用。
在这里插入图片描述

以上是关于Arduino PID库简介的主要内容，如果未能解决你的问题，请参考以下文章

Arduino入门教程第一章｜C语言入门

arduino 开发用啥编程语言

用PID和Arduino,怎么让小车走直线,自动同步左右轮胎的速度?

wiringPi简介安装

C语言和ARDUINO语言一样吗

求教，关于arduino adc不准问题

Arduino PID库简介

Arduino PID库 – 简介

初学者的PID

提高初学者的 PID – 采样时间

问题所在

解决方案

《代码》

结果

关于中断的旁注

提高初学者的 PID – Derivative Kick

问题所在

解决方案

《代码》

结果

改进初学者的 PID：调整更改

问题所在

解决方案

《代码》

结果

改善初学者的 PID：Reset Windup

问题所在

解决方案 – 步骤 1

解决方案 – 步骤 2

《代码》

结果

提高初学者的PID：开/关

问题所在

解决方案

《代码》

结果

改进初学者的 PID：初始化

问题所在

解决方案

《代码》

结果

更新：为什么不是 ITerm=0？

提高初学者的PID：方向

问题所在

解决方案

《代码》

PID 完成

嵌入式STM32利用arm-dsp库进行PID调节控制

目录

一、实验简介

1.原理

2.所用外设

二、代码

1.PWM输出配置

2.定时器触发的DMA传输的ADC

3.主体代码

三、实验结果