字符串问题

Posted 2023-04-04

字符串问题
为什么这个函数实现不了将ss中所有下标为奇数位的字母换为大写

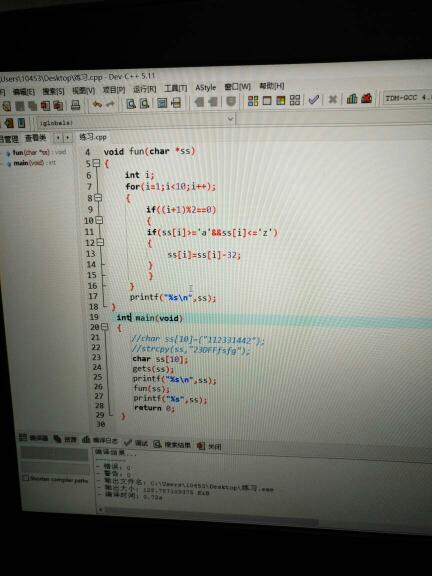
我把你的代码做了下简单修改，是可以实现将ss中所有下标为奇数位的字母换为大写的功能的；

代码如下：

#include <stdio.h>
void fun(char *ss)

int i;
for(i=1;i<10;i+=2)

if(ss[i]>=\'a\'&&ss[i]<=\'z\')
ss[i]=ss[i]-32;

printf("%s\\n",ss);

int main(void)

char ss[10];
gets(ss);
printf("%s\\n",ss);
fun(ss);
printf("%s\\n",ss);
return 0;

运行结果如下：

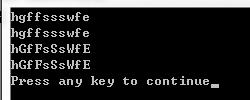
其中第一行是我输入的字符串，也就是gets(ss)一行所对应的功能；

第二行输出是main函数里第一个printf("%s\\n",ss);将所输入的字符串原封不动的再打印出来；

第三行输出是fun函数里的printf("%s\\n",ss);将替换后的字符串打印出来；

第四行输出是main函数里第二个printf("%s\\n",ss);将替换后的字符串打印出来，以验证在fun函数外部ss数组中的内容也已经改变了。

按道理来说，你的代码也是能完成替换功能的，至于为啥没替换成功，应该不是你所贴出来的这部分代码的问题。

参考技术A 有六个。
个数是总长度减去2，总长度是8，因为除了最后6个，其余每一个开始的三个字符都是一个长度为3的子串。

字符串距离问题

到目前为止，我团队赛打的很少，但有好几次团队赛都出现了字符串距离问题，作个整理。

经典的字符串距离问题，求两字符串之间的距离，两个字符串之间的距离指的是至少通过多少次操作使得这两个字符串相同。

有两个操作：

1 ：选其中一个字符串，在其任意位置插入一个任意字符；

2： 选其中一个字符串，删掉其中任意一个字符。

样例输入：

aabd

ad

样例输出 ：

2

 

做法一：正着求，用递推的方法推出，dp[i][j]表示A[1,2...i]和B[1,2...j]的距离

    for(int i = 1;i <= len_a;i++){
        for(int j = 1;j <= len_b;j++){
            if(a[i] == b[j]) {
                dp[i][j] = dp[i-1][j-1];
            }
            else dp[i][j] = min(dp[i-1][j],dp[i][j-1])+1;
        }
    }
    ans = dp[len_a][len_b];

 

做法二：先求出两个串的LCS(最长公共子串的长度),距离=两串长度和-2*LCS

    for(int i = 1;i <= len_a;i++){
        for(int j = 1;j <= len_b;j++){
            if(a[i] == b[j]) {
                lcs[i][j] = lcs[i-1][j-1]+1;
            }
            else lcs[i][j] = min(lcs[i-1][j],lcs[i][j-1]);
        }
    }
    ans = len_a+len_b-2*lcs[len_a][len_b];

我的第一次团队赛碰到了这样一题：

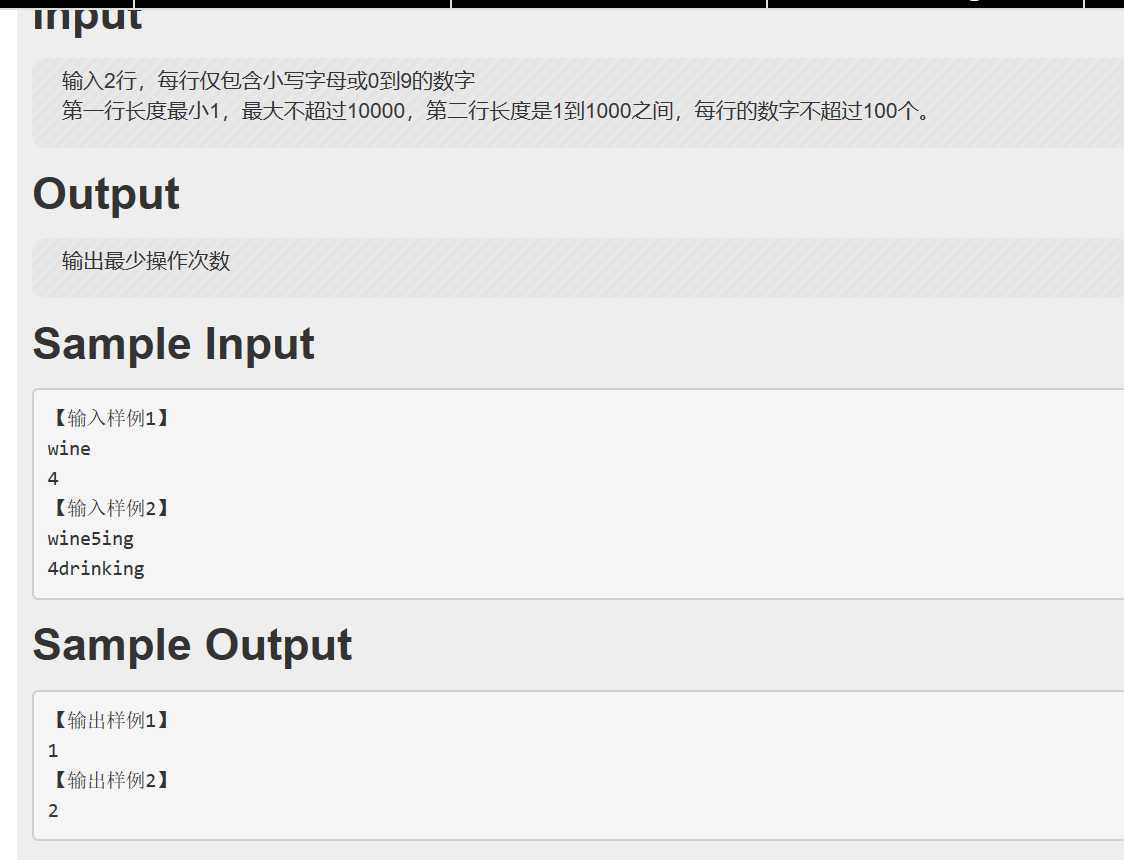
给两串字符串，含若干字母和数字,求使两个字符串相同且不含数字所需的最少操作数

操作一：任选一个字母插入到任意位置

操作二：任选一个字母删掉

操作三：把数字换成对应个数的任意字母

 

先把所有数字都展开成对应个数的‘#‘, ‘#‘可以和任意字母对应

这就转换成了求两串字符串的差距问题，正着求差距，或者先求最长公共字串都行

#include<iostream>
#include<algorithm>
using namespace std;
long long dp[12000][3000];
int main()
{
    long long res = 0;
    string a,b,s1,s2;
    s1 = "",s2="";
    cin>>a>>b;
    int lena = a.length();
    int lenb = b.length();
    for(int i = 0;i<lena;i++){
        if(a[i]<=‘9‘&&a[i]>=‘0‘){
            int x = a[i]-‘0‘;
            for(int j =1;j<=x;j++) s1+=‘#‘;
            res++;
        }
        else s1+=a[i];
    }
    for(int i = 0;i<lenb;i++){
        if(b[i]<=‘9‘&&b[i]>=‘0‘){
            int x = b[i]-‘0‘;
            for(int j =1;j<=x;j++) s2+=‘#‘;
            res++;
        }
        else s2+=b[i];
    }
    //cout<<s1<<endl<<s2<<endl;
    int len1 = s1.length();
    int len2 = s2.length(); 
    dp[0][0] = 0;
    for(int i =1;i<=len1;i++) dp[i][0] = i;
    for(int i = 1;i<=len2;i++) dp[0][i] = i;
    for(int i =1;i<=len1;i++){
        for(int j =1;j<=len2;j++){
            if(s1[i-1]==s2[j-1]||s1[i-1]==‘#‘||s2[j-1]==‘#‘) dp[i][j] = dp[i-1][j-1];
            else dp[i][j] = min(dp[i-1][j],dp[i][j-1])+1;
        }
    }
    cout<<dp[len1][len2]+res<<endl;
    return 0;
}

2020杭电多校第二场1012：

给两个串A和B，A长为n,B长为m,q次查询，每次查询给一个L,R区间，求A[L...R]和B[1...m]的距离

T组输入,T<=10,n<=1e5,m<=20,q<=1e5,1<=L<=R<=n。

看起来很难，关键抓住m很小，A[L,R]和B[1...m]的LCS<=m<=20,也就是LCS的取值范围很小,之前是用递推求出A[1...i]和B[1...j]的答案，然而这个答案的取值范围却这么小，我们可以用答案反推，其中一个串取[1...i],LCS=j时，另一个串至少要取到多少,这也是可以递推的。

L，R区间是多变的，每次查询，我们就递推一遍,f[ i ][ j ]的意义：B串取[1...i]，LCS = j时，A至少要从L取到f[ i ][ j ]。

为了能够递推，首先还要预处理一个东西：g[ i ][ j ] ：A[i...n]中字符 j 第一次出现的位置，若其一次都不出现就为INF

g数组可以从后往前递推得到

        for(int j = 0;j < 26;j++) g[n+1][j] = INF;
        for(int i = n;i ;i--){
            for(int j = 0;j < 26;j++){
                g[i][j] = g[i+1][j];
            }
            g[i][A[i]-‘a‘] = i;
        }

得到g数组后，f数组就可以递推了

f[ i ][ j ] = min(f[ i - 1 ][ j ],g[  f [ i - 1 ][ j - 1 ]+1 ][  B [ i ] -  ‘a‘ ] )

AC代码：wa了好多发才过qwq

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int MAXN = 1e5+7;
const int INF = 1e9+9;
int g[MAXN][26];
int f[21][21];
int main()
{
    int T,n,m,q,l,r;
    string A,B;
    cin>>T;
    while(T--){
        cin>>A>>B;
        n = A.length();
        m = B.length();
        A =" "+A;
        B =" "+B;
        for(int j = 0;j < 26;j++) g[n+1][j] = INF;
        for(int i = n;i ;i--){
            for(int j = 0;j < 26;j++){
                g[i][j] = g[i+1][j];
            }
            g[i][A[i]-‘a‘] = i;
        }
        cin>>q;
        while(q--){
            scanf("%d%d",&l,&r);
            f[0][0] = l-1;//起点 
            for(int i = 1;i <= m;i++){
                f[i][0] = l-1;//起点 
                for(int j = 1;j <= i && j <= n;j++){
                    if(j==i){
                        if(f[i-1][j-1]>= r) f[i][j] = INF;
                        else f[i][j] = g[f[i-1][j-1]+1][B[i]-‘a‘];
                    }
                    else {
                        if(f[i-1][j-1]>= r) f[i][j] = INF;
                        else f[i][j]=min(f[i-1][j],g[f[i-1][j-1]+1][B[i]-‘a‘]);
                    }
                }
            }
            int gg = 0;
            for(int j = 1;j <= m && j <= n;j++){
                if(f[m][j]<=r) gg = j;
                else break;
            }
            printf("%d
",r-l+1+m-2*gg);
        }
    }    
    return 0;
}