教你一文解决 js 数字精度丢失问题

Posted 2023-04-04 韩旭在努力

文章目录

• • 一、关于为什么要解决精度丢失
  • 二、怎么解决js的计算精度丢失问题？
  • 三、toPrecision 特定方法返回四舍五入长度字符串
  • 结语

一、关于为什么要解决精度丢失

可以看下例子，因为js失去精度问题也是常见的问题，正常我们可以四舍五入或者 toFixed保留小数这种去解决

现在遇到问题是我们明知道计算结果是等于0.01的但是最后的结果确实true，如果我们遇到运算问题，小数数值比对问题，那么我们就必须要去解决他，否则也就会出现上者情况，出现逻辑判断出错问题

二、怎么解决js的计算精度丢失问题？

正常来说如果是 小数点保留后2位、3位等等，我们可以使用常见的 * 百位数、千位数 实现整位结果后 将结果在除以对应的数位实现结果，如下

console.log(5.22 - 5.21);

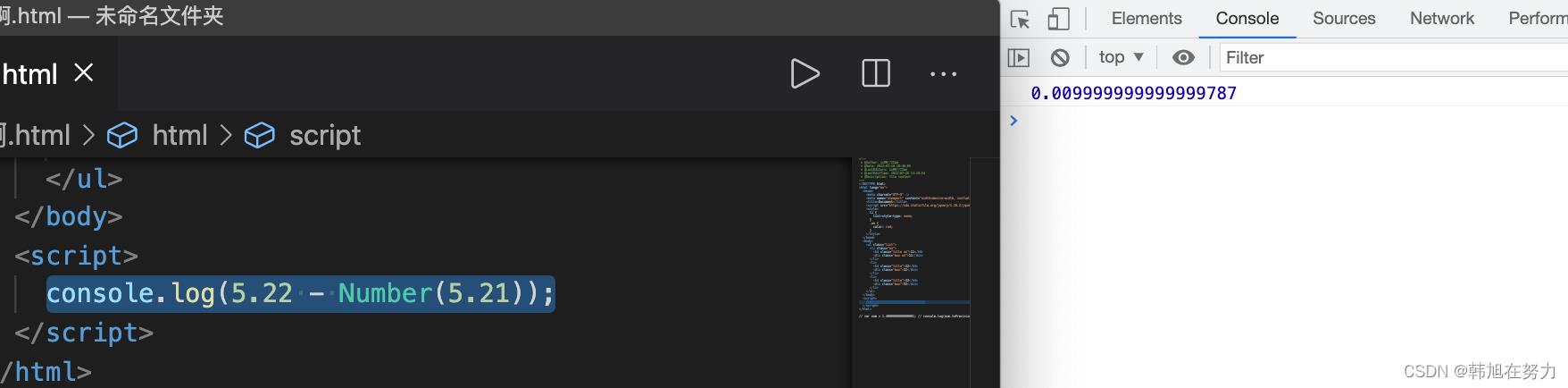
 console.log((5.22 * 100 - 5.21 * 100) / 100);

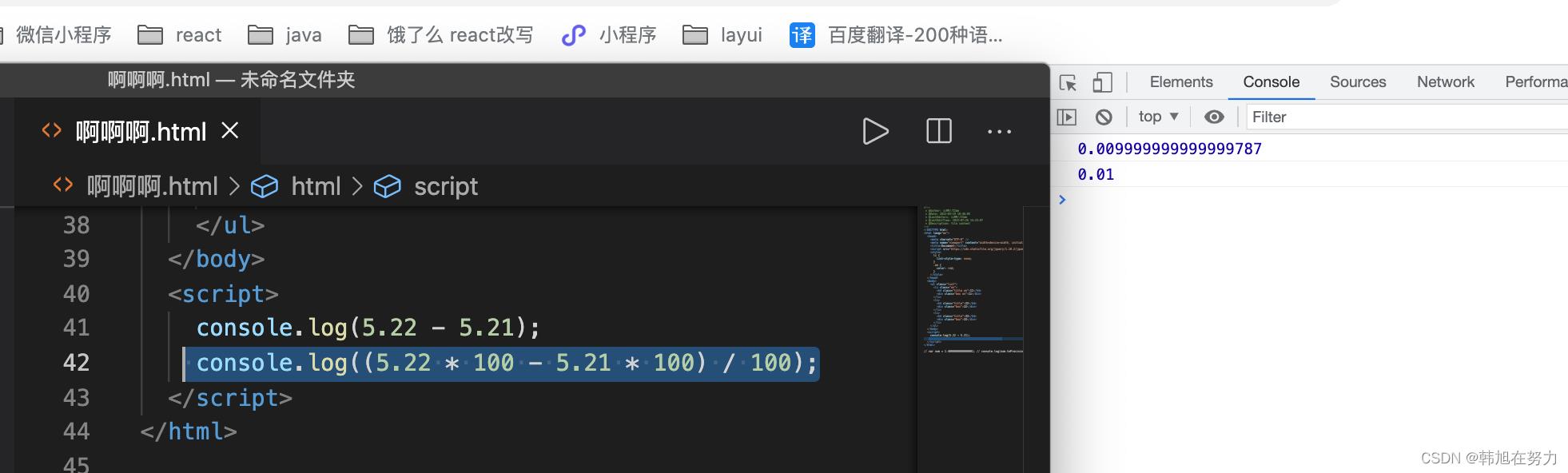
根据上方的描述我们再去着眼看我们最开始的例子

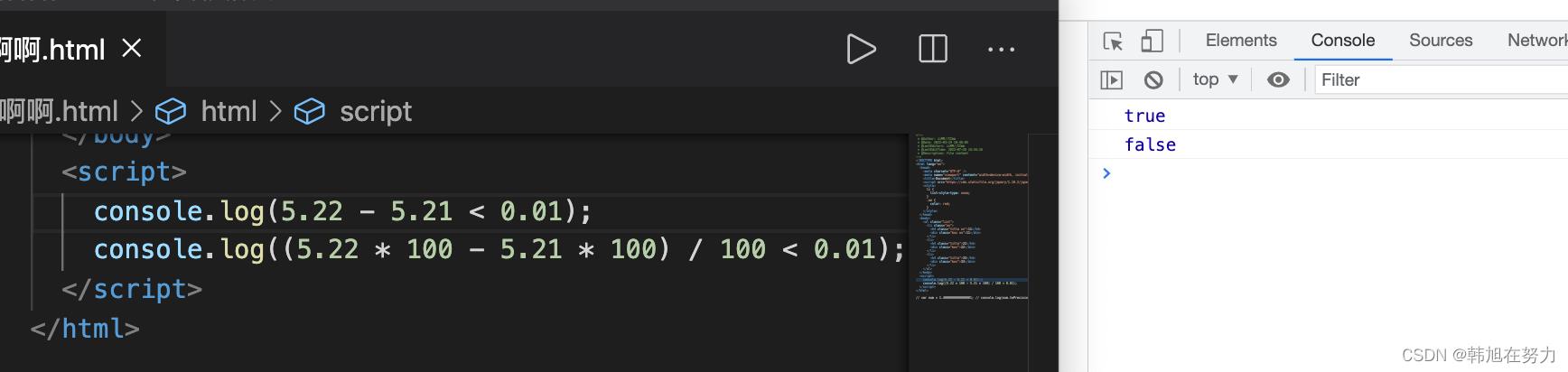
结果也就成了我们想要的结果

三、toPrecision 特定方法返回四舍五入长度字符串

当然toFixed也是可以实现对应的长度取舍效果的，因为各大浏览器针对toFixed的各类结果都是不同的有兴趣的同学可以参考下下面这篇文章
toFixed详解

在这里我们只介绍 toPrecision 参照方法详解

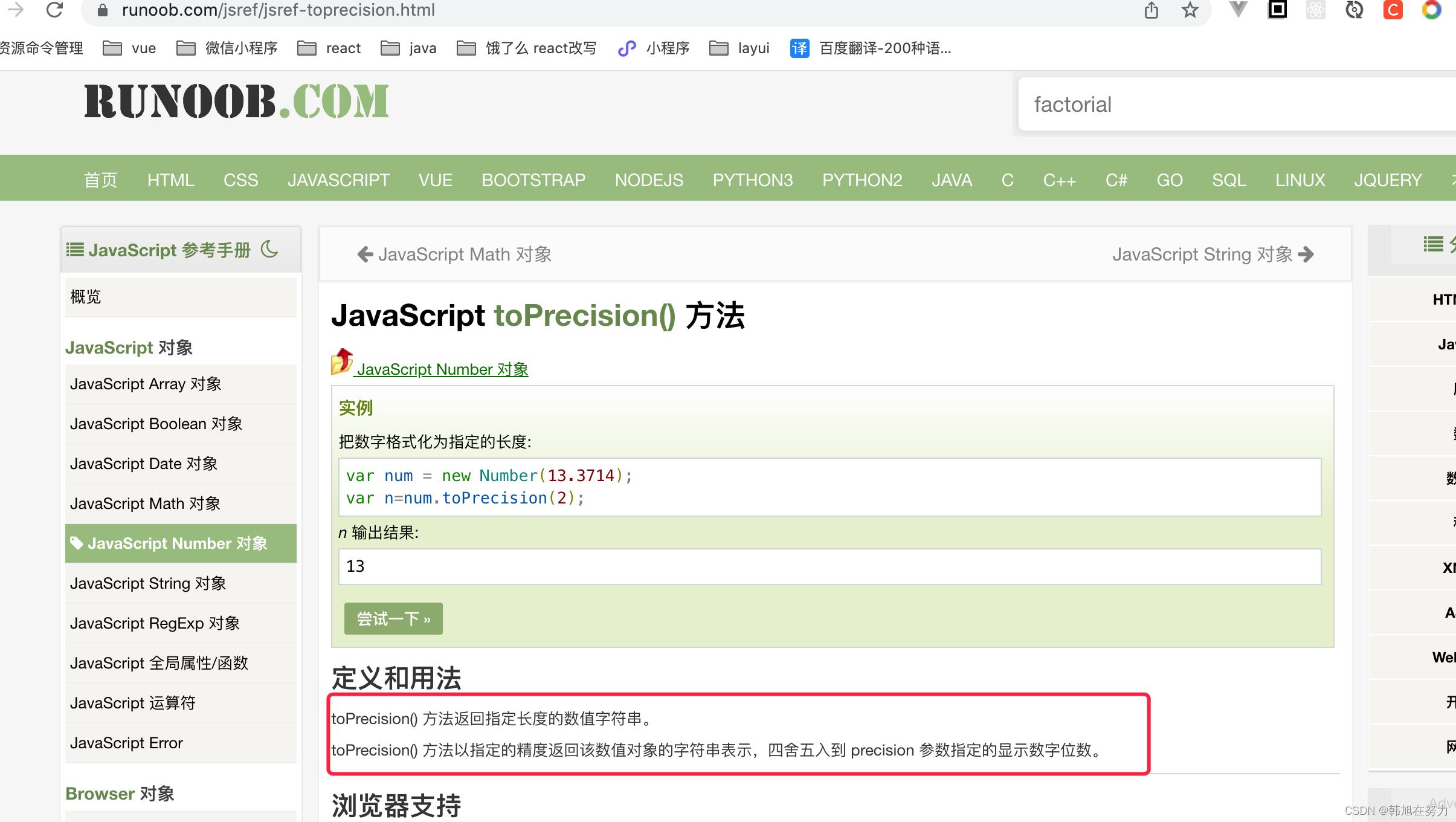
那么我们也就知道了此方法是用来干什么的
当然再有一点也就是从左到右 不为0的位置开始计算

上方举例 我们的结果是0.01

如果我们去使用toPrecision的话，那么要填写的参数则为1

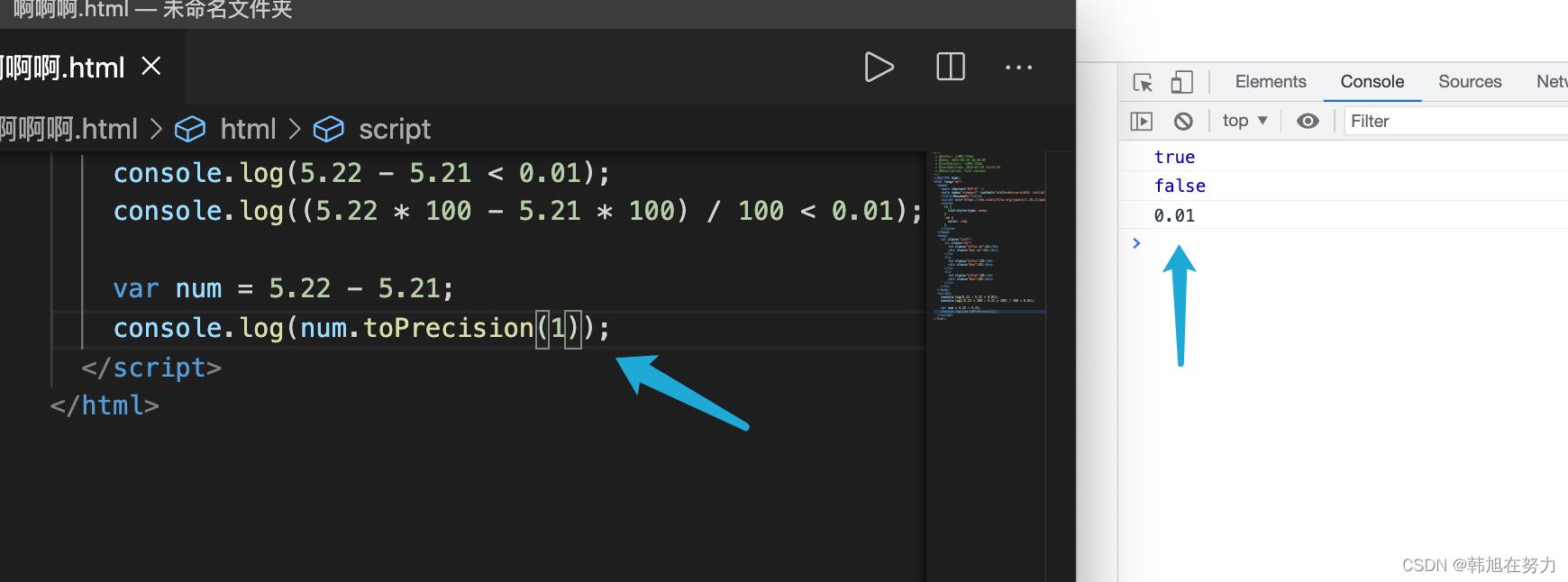
返还的结果也就是我们想要的 0.01

然后我们搭配 parseFloat 对字符串进行一个浮点数值转换后，然后对比得出最后结果

console.log(5.22 - 5.21 < 0.01);
console.log((5.22 * 100 - 5.21 * 100) / 100 < 0.01);
var num = 5.22 - 5.21;
console.log(parseFloat(num.toPrecision(1)) < 0.01);

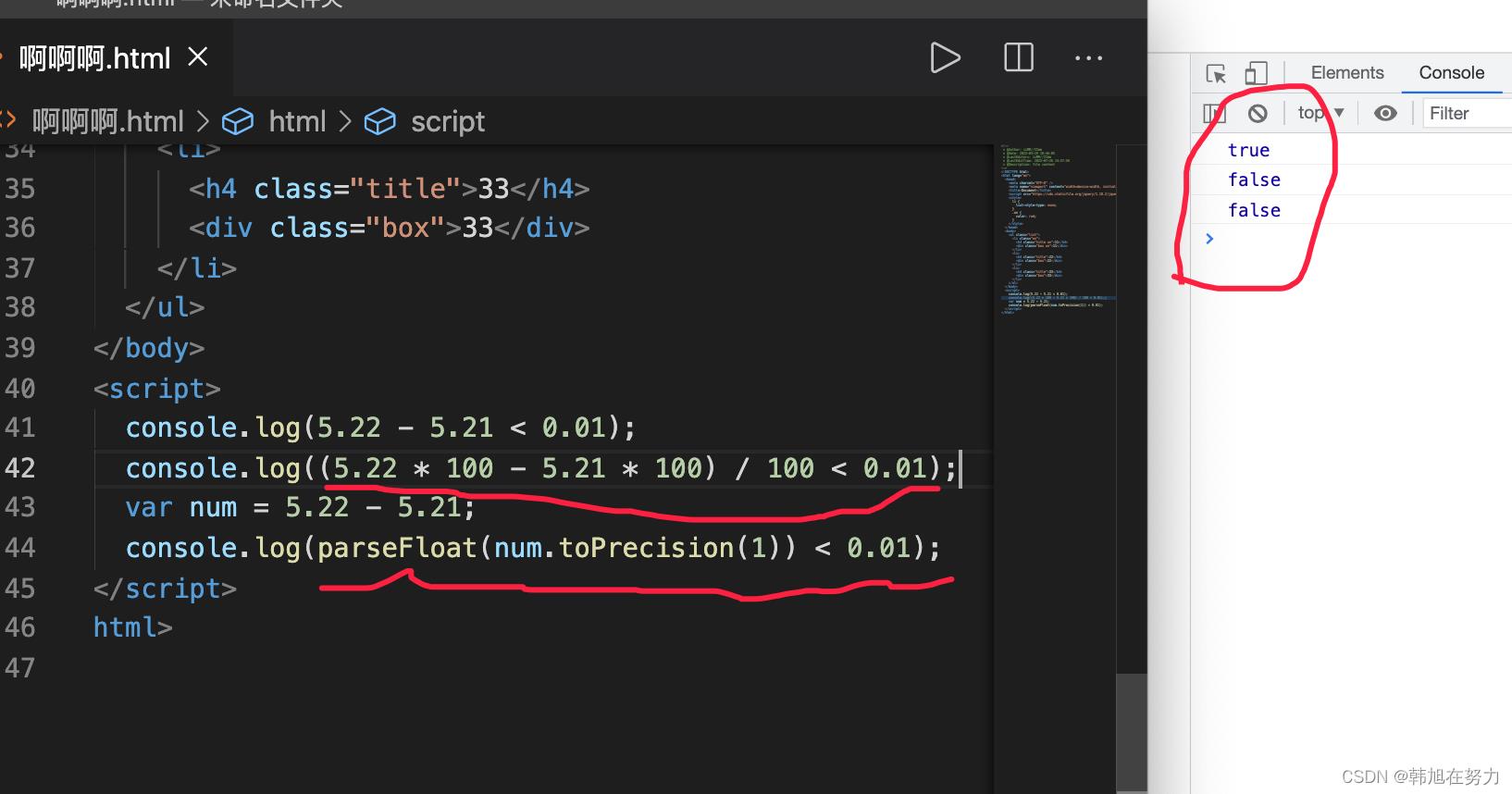
结语

✨ 每天创作一点点
✨ 开心快乐一整天
✨ 点赞关注加收藏
✨ 美好一天又一天

铁铁们 感谢支持 我需要你们的三连 👍👍👍

js数字位数太大导致参数精度丢失问题

 

 

最近遇到个比较奇怪的问题，js函数里传参，传一个位数比较大，打印arguments可以看到传过来的参数已经改变。

 

然后查了一下，发现确实是js精度丢失造成的。我的解决方法是将数字型改成字符型传输，这样就不会造成精度丢失了。如下图：

 

 

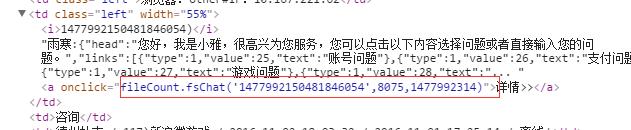
JS 数字丢失精度的原因

计算机的二进制实现和位数限制有些数无法有限表示。就像一些无理数不能有限表示，如 圆周率 3.1415926...，1.3333... 等。JS 遵循 IEEE 754 规范，采用双精度存储（double precision），占用 64 bit。如图

 

意义

• 1位用来表示符号位
• 11位用来表示指数
• 52位表示尾数

 

浮点数，比如

1 2	0.1 >> 0.0001 1001 1001 1001…（1001无限循环） 0.2 >> 0.0011 0011 0011 0011…（0011无限循环）

此时只能模仿十进制进行四舍五入了，但是二进制只有 0 和 1 两个，于是变为 0 舍 1 入。这即是计算机中部分浮点数运算时出现误差，丢失精度的根本原因。

 

大整数的精度丢失和浮点数本质上是一样的，尾数位最大是 52 位，因此 JS 中能精准表示的最大整数是 Math.pow(2, 53)，十进制即 9007199254740992。

大于 9007199254740992 的可能会丢失精度

1 2 3

9007199254740992     >> 10000000000000...000 // 共计 53 个 0 9007199254740992 + 1 >> 10000000000000...001 // 中间 52 个 0 9007199254740992 + 2 >> 10000000000000...010 // 中间 51 个 0

 

实际上

1 2 3 4

9007199254740992 + 1 // 丢失 9007199254740992 + 2 // 未丢失 9007199254740992 + 3 // 丢失 9007199254740992 + 4 // 未丢失

 

结果如图

 

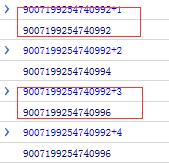
以上，可以知道看似有穷的数字, 在计算机的二进制表示里却是无穷的，由于存储位数限制因此存在“舍去”，精度丢失就发生了。

想了解更深入的分析可以看这篇论文（又长又臭）：What Every Computer Scientist Should Know About Floating-Point Arithmetic

 

三、解决方案

对于整数，前端出现问题的几率可能比较低，毕竟很少有业务需要需要用到超大整数，只要运算结果不超过 Math.pow(2, 53) 就不会丢失精度。

对于小数，前端出现问题的几率还是很多的，尤其在一些电商网站涉及到金额等数据。解决方式：把小数放到位整数（乘倍数），再缩小回原来倍数（除倍数）

1 2	// 0.1 + 0.2 (0.1*10 + 0.2*10) / 10 == 0.3 // true