基于MATLAB编程的蚁群算法格栅路径优化,基于蚁群算法的路径避障规划
Posted 神经网络机器学习智能算法画图绘图
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于MATLAB编程的蚁群算法格栅路径优化,基于蚁群算法的路径避障规划相关的知识,希望对你有一定的参考价值。
目录
背影
蚁群算法的原理及步骤
基本定义
编程思路
适应度函数
算法的规则
特点
主要参数
代码
结果分析
展望
背影
格栅路径优化运算量大,可能解多,求解难度高的,可行解多的特点,一般都无法用直接求解,本文用蚁群算法进行求解,蚁群算法拥有更好的全局寻优能力,
蚁群算法
基本定义
将蚁群算法应用于解决优化问题的基本思路为:用蚂蚁的行走路径表示待优化问题的可行解,整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多,随着时间的推进,较短的路径上累积的信息素浓度逐渐增高,选择该路径的蚂蚁个数也愈来愈多。最终,整个蚂蚁会在正反馈的作用下集中到最佳的路径上,此时对应的便是待优化问题的最优
编程思路
蚂蚁找到最短路径要归功于信息素和环境,假设有两条路可从蚁窝通向食物,开始时两条路上的蚂蚁数量差不多:当蚂蚁到达终点之后会立即返回,距离短的路上的蚂蚁往返一次时间短,重复频率快,在单位时间里往返蚂蚁的数目就多,留下的信息素也多,会吸引更多蚂蚁过来,会留下更多信息素。而距离长的路正相反,因此越来越多的蚂蚁聚集到最短路径上来。
蚂蚁具有的智能行为得益于其简单行为规则,该规则让其具有多样性和正反馈。在觅食时,多样性使蚂蚁不会走进死胡同而无限循环,是一种创新能力;正反馈使优良信息保存下来,是一种学习强化能力。两者的巧妙结合使智能
优化PID基于matlab混沌改进的蚁群算法求解船舶锅炉压力控制PID优化问题含Matlab源码 2303期
⛄一、获取代码方式
本文的优化算法设计思路为:将混沌优化算法应用到蚁群算法的初始环节中以此设置初始信息素值, 采取变尺度混沌局部再搜索机制和引入混沌扰动的信息素更新策略, 有效克服局部最优的缺点, 提高搜索效率。
基于改进混沌蚁群算法的设计步骤如下:
-
混沌优化算法初始化, 得到初始混沌路径。初始化蚁群规模数目为Na, 蚂蚁活动范围为[a, b], 引入随机函数以产生混沌映射的初始值x (0) 。通过Logistic映射迭代Na-1次产生混沌序列X c, 将混沌序列X c中变量分别进行载波映射得到新的混沌序列Xd, 上述过程如下:

式 (19) 中, a和b为蚁群搜索范围[a, b]的边界。最后, 将序列Xd中Na个新混沌变量利用全排列构造原理构造出Na!条不同的初始混沌路径。 -
获取初始信息素值。将通过步骤2) 产生的Na!条初始混沌路径代入步骤3) 中航路代价函数, 从中选择前Na个最小值并取倒数, 以此作为改进蚁群算法的信息素初值。
-
初始化迭代次数u=0, 最大迭代次数为Ncmax。
-
将Na只蚂蚁均置于起始点, 每只蚂蚁根据式 (11) 所示的启发函数ηij (t) 和信息素浓度函数τij (t) , 按照式 (10) 所示状态转移概率Pik, j (t) 选择下一节点, 直至所有蚂蚁均搜索到目标点, 则输出Na个航路。计算这Na个航路对应的航路代价值, 从中择优得出当前迭代次数u下的最优解。假设当前迭代次数u下的最优解为第t (t∈[1, Na]) 只蚂蚁寻找的路径, 记作Pbest (u, t) , 初始化为Pbest (u, t) 。当迭代次数u≥1时, 满足:
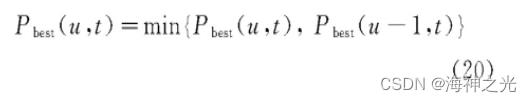
其中, Pbest (u-1, t) 为上一次迭代次数下最优解。 -
引入变尺度混沌局部再搜索机制, 进行局部再搜索。以上一步骤产生的Pbest (u, t) 为基础, 通过以下2个公式产生ε个在对应于最优解Pbest (u, t) 的搜索点附近具有混沌特性的搜索点集合W, 计算ε个搜索点的航路代价值, 并将它们与Pbest (u, t) 进行比较, 取两者的最小值替换Pbest (u, t) 。这些搜索点的计算公式如下:

-
引入混沌扰动的信息素更新策略, 对上述寻优得到的航路按下式进行全局信息素更新:

⛄二、部分源代码
clear
K=20;%迭代次数
N=10;%蚁群规模
Rho=0.95;%信息素蒸发系数,取值0~1之间,推荐取值0.7~0.95
Q=1;%信息素增加强度,大于0,推荐取值1左右
Lambda=0.2;%蚂蚁爬行速度,取值0~1之间,推荐取值0.1~0.5
LB=[2,0.5,0.8];
UB=[3,2,1.6];
Num=[1,2];
Den=[1,2,1];
Delay=0.5;
ts=0.01;
StepNum=1000;
SigType=1;
PIDLB=-10;
PIDUB=10;
%% 第二步:调用蚁群算法
[BESTX,BESTY,ALLX,ALLY]=ACOUCP(K,N,Rho,Q,Lambda,LB,UB,Num,Den,Delay,ts,StepNum,SigType,PIDLB,PIDUB);
%% 第三步:整理输出结果
bestx=BESTXK;
kp=bestx(1);
ki=bestx(2);
kd=bestx(3);
disp(‘最佳控制参数kp,ki,kd分别为’);
disp(bestx);
[J,u,yout,error]=PIDOBJ(kp,ki,kd,Num,Den,Delay,ts,StepNum,SigType,PIDLB,PIDUB);
time=ts*(1:StepNum);
if SigType1%阶跃信号
rin=ones(1,StepNum);
elseif SigType2%方波信号
rin=sign(sin(22pitime));
elseif SigType==3%正弦波信号
rin=0.5sin(22pi*time);
end
⛄三、运行结果
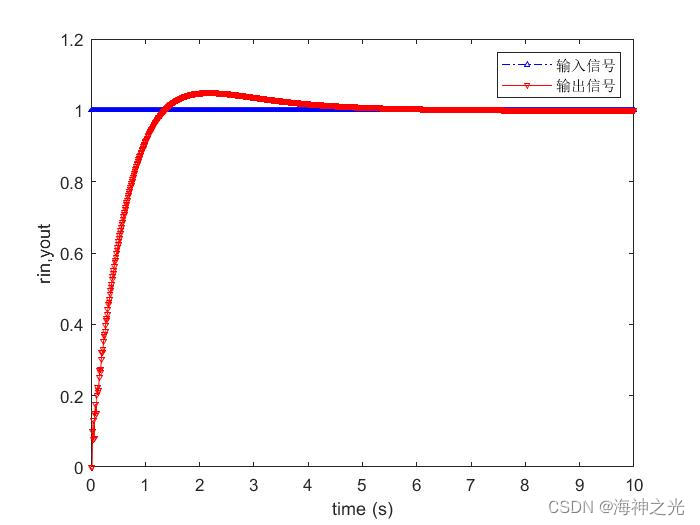


⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]刘蓉,杨帆,张衡.基于改进混沌蚁群算法的无人机航路规划[J].指挥信息系统与技术. 2018,9(06)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
以上是关于基于MATLAB编程的蚁群算法格栅路径优化,基于蚁群算法的路径避障规划的主要内容,如果未能解决你的问题,请参考以下文章