Python量化交易10——资产组合比例优化(CAMP,VAR,CVAR)
Posted 阡之尘埃
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python量化交易10——资产组合比例优化(CAMP,VAR,CVAR)相关的知识,希望对你有一定的参考价值。
案例背景
本科的金融或者投资学都会学到CAMP模型,资本资产定价模型,可是怎么用代码实现却一直没人教。
本期用Python代码案例配置一个资产组合,并且做CAMP模型,计算VAR和CVAR等指标。
(本期案例中涉及到的公司仅用于案例研究,不构成任何建议。)
数据获取
用证券宝获取gu票数据,先导入要用的包:
import baostock as bs
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.optimize as optimization
import scipy.stats as stats
plt.rcParams ['font.sans-serif'] ='SimHei' #显示中文
plt.rcParams ['axes.unicode_minus']=False #显示负号定义获取日K数据的函数:
def get_stocks_daily(stocks=['sh.601318'],start_date='2022-04-01',end_date='2023-03-29'):
lg = bs.login()
df_results=pd.DataFrame()
for stock in stocks:
rs_result = bs.query_history_k_data_plus(stock,fields="date,code,open,high,low,close,preclose,volume,amount,adjustflag,turn,tradestatus,pctChg,isST"\\
, start_date=start_date,end_date=end_date, frequency="d", adjustflag="3")
df_result = rs_result.get_data()
#df_result=df_result.set_index('date')
df_results=pd.concat([df_results,df_result],ignore_index=True)
print(f"stock获取完成")
bs.logout()
cols_to_convert = [col for col in df_results.columns if col != 'code' and col!='date']
df_results['date']=pd.to_datetime(df_results['date'])
df_results[cols_to_convert] = df_results[cols_to_convert].astype('float64')
return df_results定义获取gu票的代码列表:
stocks_lst=['sh.601318','sh.600519','sz.300750','sz.002714','sz.002603','sz.000681','sh.000300'] #中国平安,贵州茅台,宁德时代,牧原股份,以岭药业,视觉中国,最后的沪深300作为市场基础回报率。
为什么选这个几公司呢?因为他们有的是金融权重股,有的是消费白酒,还有这两年疫情炒得很热的医药,新能源,人工智能等等代表性的gu票。
获取:
data=get_stocks_daily(stocks=stocks_lst,start_date='2021-04-01',end_date='2023-03-29')
数据处理一下:
data=data[['code','date','close']].pivot(index='date',columns='code', values='close')[stocks_lst]\\
.set_axis(['中国平安','贵州茅台','宁德时代','牧原股份','以岭药业','视觉中国','沪深300'],axis='columns')
data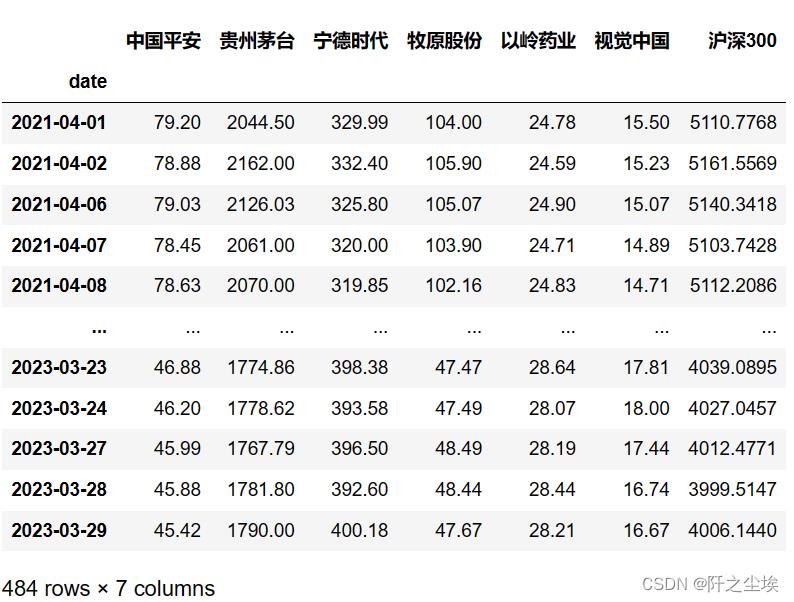
描述性统计
画出他们的价格走势:
colors=['c', 'b', 'g', 'tomato', 'm', 'y', 'lime', 'k','orange','pink','grey','tan','purple']
fig, ax = plt.subplots(4,2,figsize=(8,7),dpi=256)
for i,col in enumerate(data.columns):
n=int(str('42')+str(i+1))
plt.subplot(n)
df_col=data[col]
plt.plot(df_col,label=col,color=colors[i])
plt.xticks(rotation=20)
plt.title(f'col的价格走势')
plt.tight_layout()
plt.show()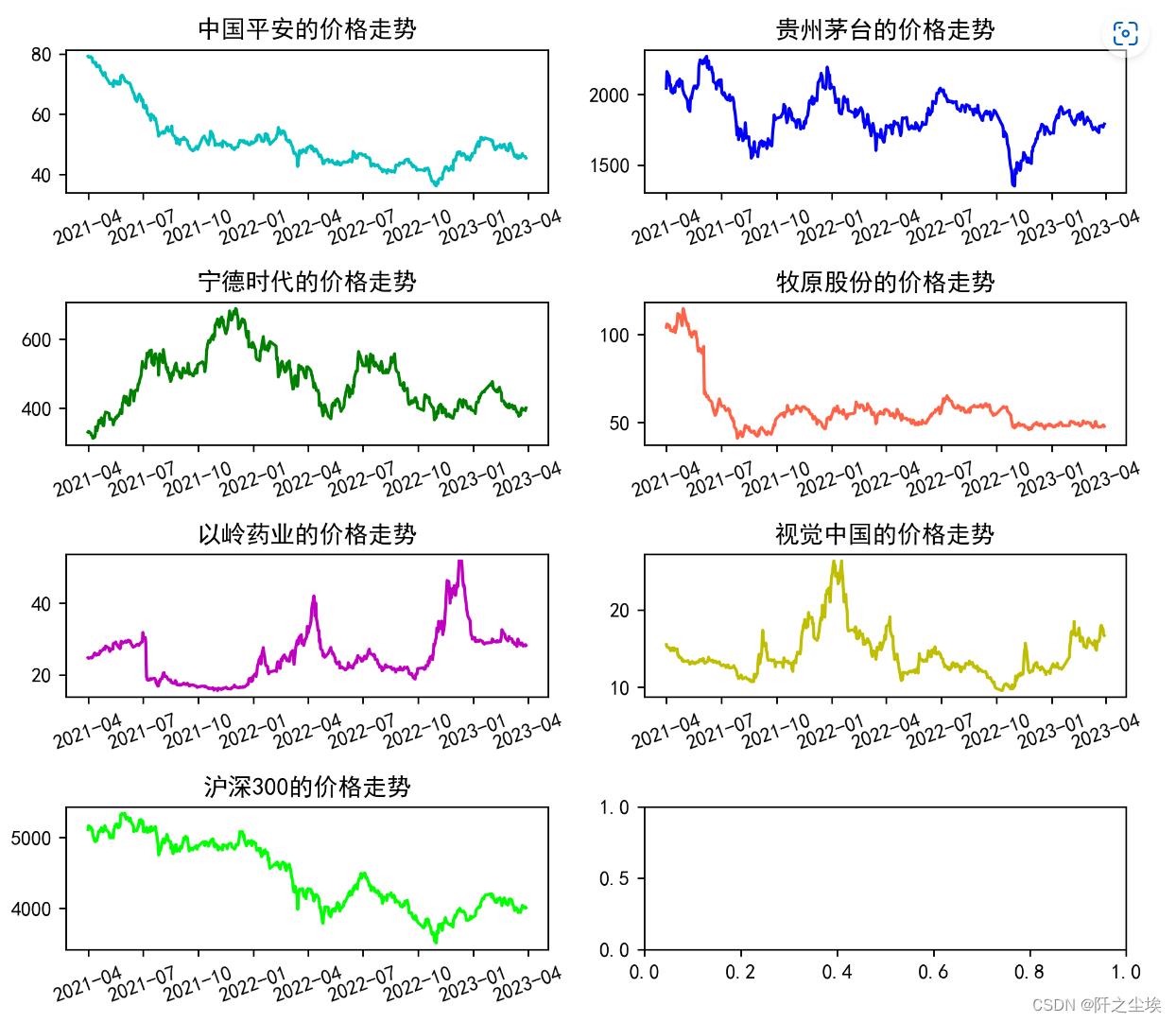
计算他们的日度收益率:
data1=pd.DataFrame(columns=data.columns)
for col in data.columns:
data1[col]=data[col].pct_change()
data1=data1.dropna()
data1.head()
同样画出他们的图:
fig, ax = plt.subplots(4,2,figsize=(8,7),dpi=256)
for i,col in enumerate(data1.columns):
n=int(str('42')+str(i+1))
plt.subplot(n)
df_col=data1[col]
plt.plot(df_col,label=col,color=colors[i])
plt.xticks(rotation=20)
plt.title(f'col的日度收益率')
plt.tight_layout()
plt.show()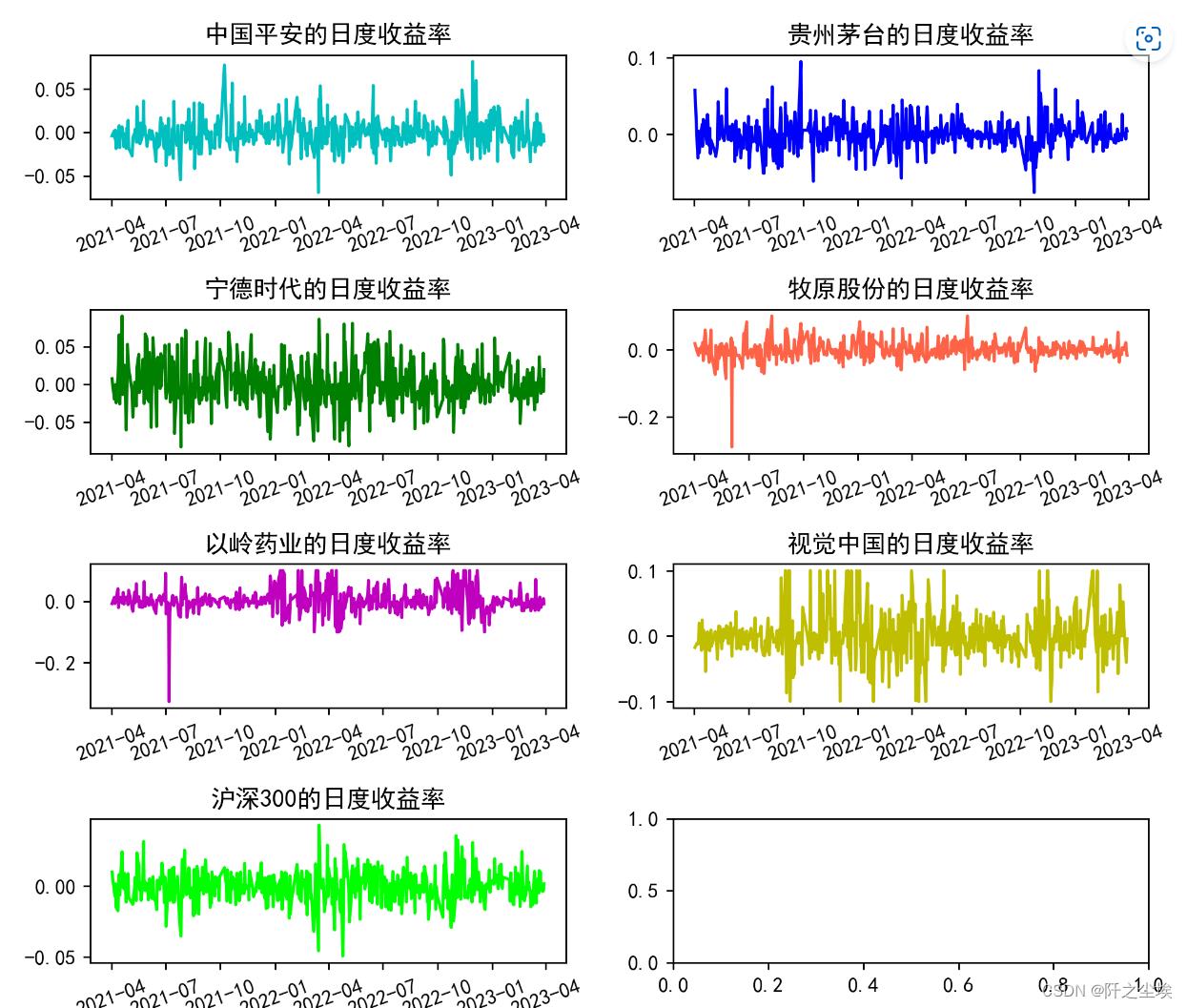
投资组合
我们都知道特征组合就是一样资产买一点....所以核心是 每种资产都买多少?这个比例是关键。
我们先随机给一个权重比例看看:
weights = np.random.random(len(stocks_lst)-1)
weights /= np.sum(weights)
weights
计算投资组合的价格和收益率:
data['portfolio']=(data.iloc[:,:-1]*weights).sum(axis=1)
data1['portfolio']=data['portfolio'].pct_change().dropna()计算他们所有资产这两年的收益率:
#这两年的收益率
(data.iloc[-1,:]-data.iloc[0,:])/data.iloc[0,:]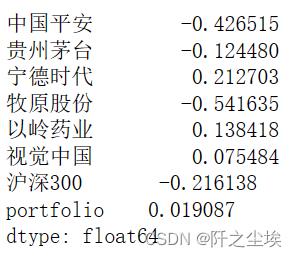
当然也可以这样算,但是我感觉这样直接相加不准:
data1.sum() #这样不准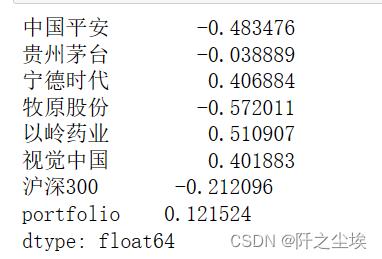
计算他们的波动性:
#这两年的波动性
data1.std()
优化投资组合比例
我们要选择一个最优的投资组合,无非是最大的收益率,或者最小的波动率。
有一个指标可以结合他们,叫夏普比率,表示每承担一单位风险所获得的回报。
# optimal portfolio sharpe ratio
noa=len(stocks_lst)-1
rf = 0.04
def statistics(weights,risk_free=0.04):
data['portfolio']=(data.iloc[:,:noa]*weights).sum(axis=1)
data1['portfolio']=data['portfolio'].pct_change().dropna()
port_returns = (data['portfolio'][-1]-data['portfolio'][0])/data['portfolio'][0]
port_variance = data1['portfolio'].std()
return np.array([port_returns, port_variance, (port_returns-risk_free*2)/port_variance])
#最小化夏普指数的负值
#Minimize the negative value of the Sharpe Index
def min_sharpe(weights):
return -statistics(weights)[2]比如我等权给一个比例,然后计算上面的指标:
statistics(weights=[1/6]*6,risk_free=0.04)
选择开始优化,最大化夏普比率,也就是最小化夏普比率负数:
# constraints an bounds
cons = ('type':'eq', 'fun':lambda x: np.sum(x)-1)
bnds = tuple((0,1) for x in range(noa))
opts = optimization.minimize(min_sharpe, noa*[1./noa,],method = 'SLSQP',bounds = bnds, constraints = cons,options='maxiter': 100000)
print("Optimal weights:", opts['x'].round(4))
print("Expected return, volatility and Sharpe ratio:", statistics(opts['x'])) 
好家伙,直接给我扔掉了4个公司......只有两个公司被选入了。
如果最小化方差会是一个怎么样的组合呢:
# Minimal variance
np.set_printoptions(suppress=True)
def min_variance(weights):
return statistics(weights)[1]
optv = optimization.minimize(min_variance,noa*[1./noa],method = 'SLSQP',
bounds = bnds, constraints = cons,options='maxiter': 100000)
print("Optimal weights:", optv['x'].round(4))
print("Expected return, volatility and Sharpe ratio:", statistics(optv['x']))
emmm,收益率太低。我们还是选第一个组合吧。
资本资产定价模型CAMP
CAMP模型很简单,公式懒得去word里面写了,我直接用python用图画一个公式:
plt.figure(figsize=(2.7,0.7),dpi=200)
plt.text(0.1, 0.4,fr'$E(R_i)=R_f+\\beta_i[E(R_m)-R_f]$')
plt.xticks([]) ;plt.yticks([])
plt.show()
所有资产都进行拟合:
df_all=pd.DataFrame(columns=['alpha','beta'])
plt.subplots(4,2,figsize=(12,12),dpi=256)
for i,col in enumerate(data1.columns):
if col!='沪深300':
n=int(str('42')+str(i+1))
plt.subplot(n)
b,a=np.polyfit(data1['沪深300'], data1[col], deg=1)
#plt.figure(figsize=(4,2.5),dpi=128)
plt.scatter(data1['沪深300'], data1[col], label="Data points")
plt.plot(data1['沪深300'], a + b*data1['沪深300'], color='green', label="CAPM Line")
plt.title(f'col Capital Asset Pricing Model', fontsize=14)
plt.xlabel('Market return $r_m$', fontsize=14)
plt.ylabel(f'col return $r_i$', fontsize=14)
plt.text(0, 0.05, fr'$r_i = a.round(3) + b.round(3) r_m$', color='red', fontsize=14)
plt.legend()
plt.axvline(color="red",linestyle="dashed",linewidth=2.5)
plt.axhline(color="red",linestyle="dashed",linewidth=2.5)
plt.grid(True, axis='both')
df_all.loc[col,:]=[a,b]
plt.tight_layout()
plt.show()
查看计算的阿尔法和贝塔值
df_all #查看计算的阿尔法和贝塔值
用公式计算期望收益率
rm = data1['沪深300'].mean() * 252
rf+df_all.loc['中国平安','beta'] * (rm-rf)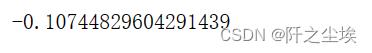
rf+df_all.loc['贵州茅台','beta'] * (rm-rf)
rf+df_all.loc['portfolio','beta'] * (rm-rf)
计算VAR和CVAR
定义一个var函数,然后再定义一个一体化函数,var和cvar都算出来,然后画图:
def VaR_r(mu,sigma,q,n):
z=stats.norm.ppf(q)
return (mu*n)+((sigma*np.sqrt(n))*z)def deal_stock(series=data['贵州茅台'],stock_name='贵州茅台'):
AMZN_returns = np.log(series) - np.log(pd.Series(series).shift(1))
mu = np.mean(AMZN_returns) ; sigma = np.std(AMZN_returns)
#var
AMZN_VaR_1day=VaR_r(mu,sigma,0.01,1) ; AMZN_VaR_60day=VaR_r(mu,sigma,0.01,60)
print(f"stock_name 1day var is AMZN_VaR_1day, 60days var is AMZN_VaR_60day")
#CVaR
AMZN_cvar_1day=AMZN_returns[AMZN_returns <= AMZN_VaR_1day].mean()
AMZN_returns60 = AMZN_returns*60
AMZN_cvar_60day=AMZN_returns60[AMZN_returns60 <= AMZN_VaR_60day].mean()
print(f"stock_name 1day cvar is AMZN_cvar_1day, 60days cvar is AMZN_cvar_60day")
# VaR_1day & cvar 1day
plt.subplots(1,2,figsize=(14,5),dpi=200)
plt.subplot(121)
plt.hist(AMZN_returns[AMZN_returns < AMZN_VaR_1day], bins=20,label='In var')
plt.hist(AMZN_returns[AMZN_returns > AMZN_VaR_1day], bins=20,label='Out var')
plt.axvline(AMZN_VaR_1day, color='blue', linestyle='dashed', linewidth=1,label=f"stock_name Var 1day")
plt.axvline(AMZN_cvar_1day, color='k', linestyle='dashed', linewidth=1,label=f"stock_name CVaR 1day")
plt.text(AMZN_VaR_1day, 40, f'stock_name_VaR_1day=round(AMZN_VaR_1day,3)', color='black', fontsize=15, horizontalalignment='center', verticalalignment='center')
plt.text(AMZN_cvar_1day, 20, f'stock_name_CVaR_1day=round(AMZN_cvar_1day,3)', color='blue', fontsize=15, horizontalalignment='center', verticalalignment='center')
plt.title(f'1 day VaR & CVaR of stock_name(99%)')
plt.legend()
plt.xlabel('return')
plt.ylabel('frequency')
# VaR_60day & CVaR_60day
plt.subplot(122)
plt.hist(AMZN_returns60[AMZN_returns60 < AMZN_VaR_60day], bins=20,label='In var')
plt.hist(AMZN_returns60[AMZN_returns60 > AMZN_VaR_60day], bins=20,label='Out var')
plt.axvline(AMZN_VaR_60day, color='b', linestyle='dashed', linewidth=1,label=f"stock_name Var 60day")
plt.axvline(AMZN_cvar_60day, color='k', linestyle='dashed', linewidth=1,label=f"stock_name CVar 60day")
plt.text(AMZN_VaR_60day, 30, f'stock_name_VaR_60day=round(AMZN_VaR_60day,3)', color='black', fontsize=15, horizontalalignment='center', verticalalignment='center')
plt.text(AMZN_cvar_60day, 20, f'stock_name_CVaR_60day=round(AMZN_cvar_60day,3)', color='blue', fontsize=15, horizontalalignment='center', verticalalignment='center')
plt.title(f'60 day VaR & CVaR of stock_name(99%)')
plt.legend()
plt.xlabel('return')
plt.ylabel('frequency')
plt.tight_layout()
plt.show()
#return AMZN_VaR_1day,AMZN_VaR_60day,AMZN_cvar_1day,AMZN_cvar_60day,AMZN_returnsdeal_stock(series=data['中国平安'],stock_name='中国平安')
带进去就行。用起来很方便
deal_stock(series=data['贵州茅台'],stock_name='贵州茅台') 
其他的不展示了,就展示一下投资组合的吧:
deal_stock(series=data['portfolio'],stock_name='portfolio')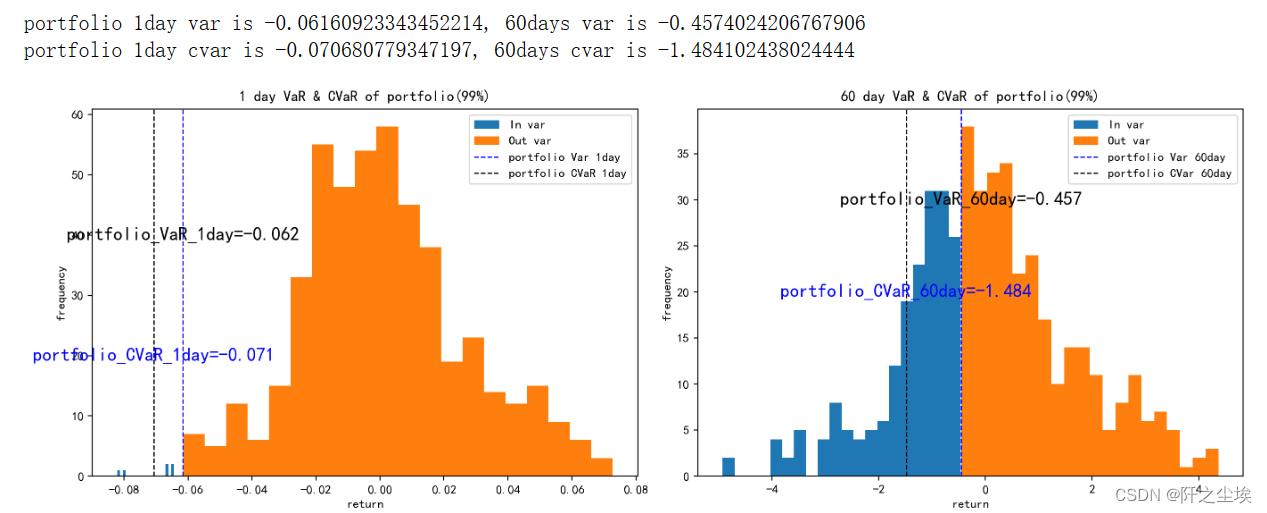
Python量化交易:投资组合
- Python量化交易入门
- 量化交易的历史
- Python量化交易项目怎么做
- Python量化交易之回测框架介绍
- Python量化交易:策略创建运行流程
- Python量化交易:数据获取接口
- Python量化交易:回测交易接口
文章目录
学习目标:
说明投资组合的定义
了解投资组合的市场价值和资金价值
那么当我们选好了股票之后,其实就可以选择购买或者卖出了。但是注意了这里所说的交易,是在历史数据当中回测的时候去每天判断交易。并不是后面的模拟交易或者实盘交易。
投资组合
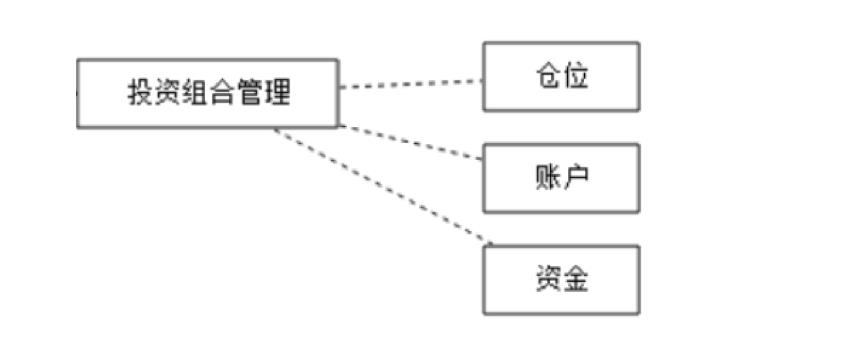
一、定义
投资组合是由投资人或金融机构所持有的股票、债券、金融衍生产品等组成的集合,目的是分散风险。
二、如何查看投资组合信息
还记得我们之前提到的一个叫context的参数吗,这个参数当中就包含了投资组合的信息
context属性
now - 当前时间
context.now
使用以上的方式就可以在handle_bar中拿到当前的bar的时间,比如day bar的话就是那天的时间,minute bar的话就是这一分钟的时间点。
返回数据类型为datetime.datetime
portfolio - 投资组合信息
context.portfolio
该投资组合在单一股票或期货策略中分别为股票投资组合和期货投资组合。在股票+期货的混合策略中代表汇总之后的总投资组合。
stock_account - 股票资金账户信息
context.stock_account
获取股票资金账户信息。
portfolio对象
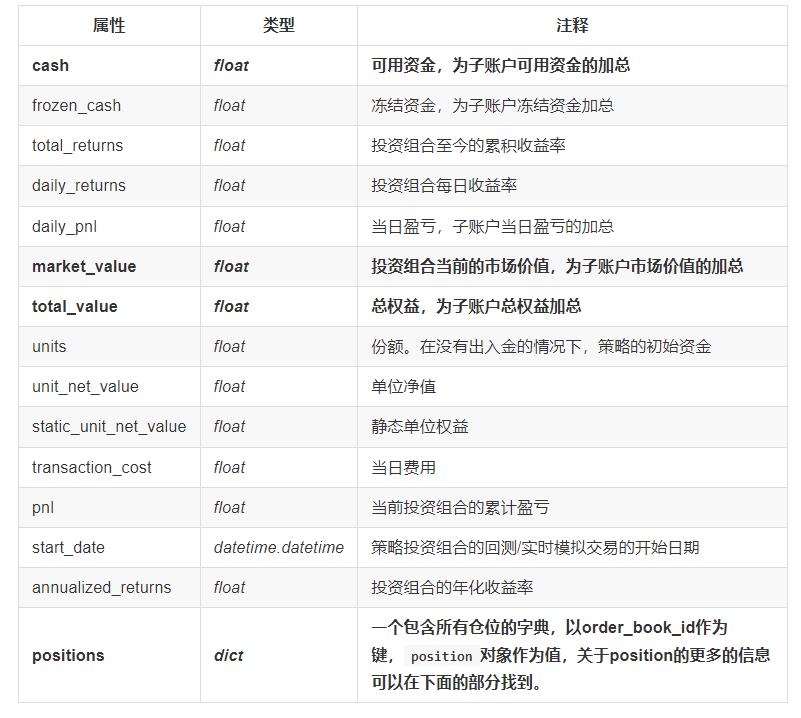
股票position对象
position就代表着当前我们的仓位中有哪些股票正持有,position.keys()可以获取

三、代码
# 查看我们的投资组合信息,仓位、资金
# 查看股票账户信息
logger.info("股票账户信息:")
logger.info(context.stock_account)
# 卖出股票就要从持有的这些股票当中去选择
logger.info(context.portfolio.positions)
# 交易的价格计算
# 当日的:close * 股数
logger.info("投资组合的资金:%f" % context.portfolio.cash)
logger.info("投资组合的市场价值:%f" % context.portfolio.market_value)
logger.info("投资组合的总价值:%f" % context.portfolio.total_value)
四、查看交易情况界面
以上是关于Python量化交易10——资产组合比例优化(CAMP,VAR,CVAR)的主要内容,如果未能解决你的问题,请参考以下文章