172. 阶乘后的零——Leetcode每日一题

Posted 2023-04-03 期望上岸的鱼

172. 阶乘后的零

给定一个整数 n ，返回 n! 结果中尾随零的数量。

提示 n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1

示例 1：

输入：n = 3
输出：0
解释：3! = 6 ，不含尾随 0

示例 2：

输入：n = 5
输出：1
解释：5! = 120 ，有一个尾随 0

示例 3：

输入：n = 0
输出：0

提示：

• $0<=n<=10^4$

进阶：你可以设计并实现对数时间复杂度的算法来解决此问题吗？

思路：

• 尾部的 0 由 2 * 5 得来，2 的数量明显多于 5 的数量，因此只要统计有多少个 5 即可。

优化进阶：

• 对于一个数 N，它所包含 5 的个数为：$N/5+N/5^2+N/5^3+...$，其中 N/5 表示不大于 N 的数中 5 的倍数贡献一个 5，$N/5^2$ 表示不大于 N 的数中$5^2$ 的倍数再贡献一个 5 …。

例如：当N为25时， 包含5个数字为：

5、10、15、20、25

总个数为：$25/5+25/5^2=6$

类比：

• 如果统计的是 N! 的二进制表示中最低位 1 的位置，只要统计有多少个 2 即可；
• 2 的个数为: $N/2+N/2^2+N/2^3+...$

代码：(Java)

public class TrailingZeroes 

	public static void main(String[] args) 
		// TODO Auto-generated method stub
		int n = 5;
		System.out.println(trailingZeroes(n));
	
	
	public static int trailingZeroes(int n) 
		
		int num = 0;
		for(int i = n; i > 0; i--) 
			int j = i;
			while(j % 5 == 0) 
				j /= 5;
				num++;
			
		
		
		return num;
    

优化进阶：

public class TrailingZeroes 

	public static void main(String[] args) 
		// TODO Auto-generated method stub
		int n = 5;
		System.out.println(trailingZeroes(n));
	
	
	public static int trailingZeroes(int n) 
		
		return n == 0 ? 0 : n / 5 + trailingZeroes(n / 5);
    

运行结果：

复杂度分析：

• 时间复杂度：$O(logn)$优化进阶后的，优化前的为$O(n)$.
• 空间复杂度：忽略递归带来的额外空间开销，复杂度为 $O(1)$.

题目来源：力扣。

注：仅供学习参考， 如有不足，欢迎指正！

LeetCode.172- 阶乘后的零

阶乘后的零

• 1.计算阶乘
• 2.计算因子 5

题目描述：

给定一个整数 n，返回 n! 结果尾数中零的数量。

1.计算阶乘

这种方法速度太慢了，但却是一个好的起点。虽然不会在面试中实现它，但是你可以简单的描述它是个解决问题的办法之一。
解决这个问题的最简单的办法就是计算 n!，然后计算它的末尾数 0 个数。阶乘是通过将所有在 1 和 n 之间的数字相乘计算的。例如：10!=10⋅9⋅8⋅7⋅6⋅5⋅4⋅3⋅2⋅1=3,628,800。因此，可以使用以下算法迭代计算阶乘。

代码展示：

Python

def trailingZeroes(self, n: int) -> int:  
    # Calculate n!
    n_factorial = 1
    for i in range(2, n + 1):
        n_factorial *= i
    
    # Count how many 0's are on the end.
    zero_count = 0
    while n_factorial % 10 == 0:
        zero_count += 1
        n_factorial //= 10
        
    return zero_count

在 Java 中，我们需要使用 BigInteger，防止在计算阶乘的过程中溢出。

import java.math.BigInteger;

public int trailingZeroes(int n) {
    
    // Calculate n!
    BigInteger nFactorial = BigInteger.ONE;
    for (int i = 2; i <= n; i++) {
        nFactorial = nFactorial.multiply(BigInteger.valueOf(i));
    }
                    
    // Count how many 0's are on the end.
    int zeroCount = 0;
    
    while (nFactorial.mod(BigInteger.TEN).equals(BigInteger.ZERO)) {
        nFactorial = nFactorial.divide(BigInteger.TEN);
        zeroCount++;
    }
    
    return zeroCount;
}

2.计算因子 5

这种方法也太慢了，但是在解决问题的过程中，它很可能是提出对数方法的一个步骤。
与方法 1 中那样计算阶乘不同，我们可以认识到阶乘末尾的每个 0 表示乘以 10。
那么，我们在计算 n! 时乘以 10 的次数是多少？两个数字 aa 和 bb 相乘。例如，要执行 42⋅75=3150，可以重写如下：542⋅75=2⋅3⋅7⋅3⋅5⋅5
现在，为了确定最后有多少个零，我们应该看有多少对 22 和 55 的因子。在上面的例子中，我们有一对 22 和 55 的因子。

例如，如果 n=16，我们需要查看 1到 16 之间所有数字的因子。我们只对 2 和 5 有兴趣。包含 5因子的数字是 5，10，15，包含因子 22 的数字是 2、4、6、8、10、12、14、16。因为只三个完整的对，因此 16! 后有三个零。

class Solution:
   def trailingZeroes(self, n: int) -> int:
        five = 0
        two = 2
        for i in range(5, n+1):
            cur = i
            while cur % 5 == 0:
                five += 1
                cur //= 5 
                
        for i in range(2, n+1):
            cur = i
            while cur % 2 == 0:
                two += 1
                cur //= 2

        return min(two, five)

这样我们就得到了正确答案，但是我们仍然可以做一些改进。

首先，我们可以注意到因子 2 数总是比因子 5 大。为什么？因为每四个数字算作额外的因子 2，但是只有每 25 个数字算作额外的因子 5。下图我们可以清晰的看见：

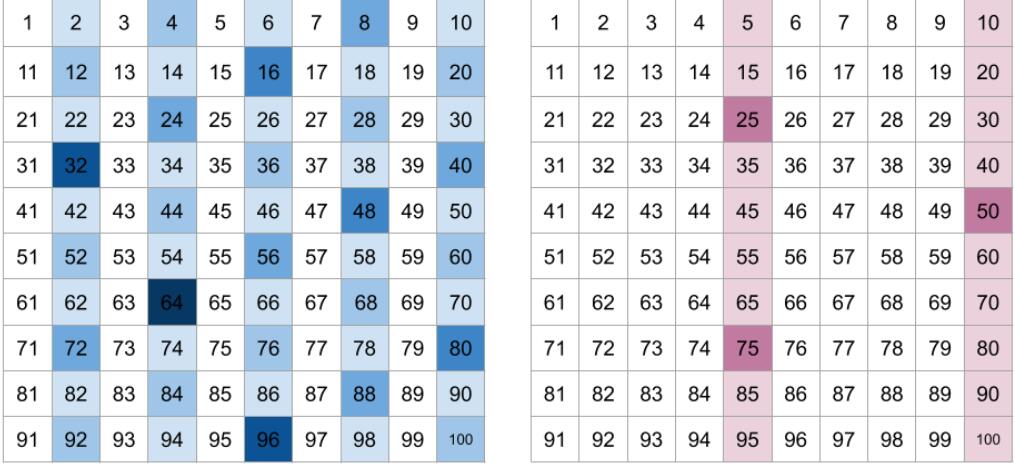
优化1

class Solution:
   def trailingZeroes(self, n: int) -> int:
        five = 0
 
        for i in range(5, n+1):
            cur = i
            while cur % 5 == 0:
                five += 1
                cur //= 5 

        return five

优化2
我们可以做最后一个优化。在上面的算法中，我们分析了从 1 到 n 的每个数字。但是只有 5, 10, 15, 20, 25, 30, … 等等 至少有一个因子 5。所以，偶们不必一步一步的往上迭代，可以五步的往上迭代：因此可以修改为：

def trailingZeroes(self, n: int) -> int:
        
    zero_count = 0
    for i in range(5, n + 1, 5):
        current = i
        while current % 5 == 0:
            zero_count += 1
            current //= 5

    return zero_count

优化3
在方法 2 中，我们找到了一种计算阶乘后的零的个数的方法，而不需要实际计算阶乘。这是通过在 55 的每个倍数上循环，从 5 到 n，并计算 5 的每个倍数中有多少个因子。我们把所有这些数字加起来得到最终结果。

然而，无论是实际上还是对问题的要求来说，方法 2 仍然太慢。为了得出一个足够快的算法，我们需要做进一步改进，这个改进能使我们在对数时间内计算出我们的答案。

def trailingZeroes(self, n: int) -> int:
    zero_count = 0
    while n > 0:
        n //= 5
        zero_count += n
    return zero_count

摘自官方题解 Link