二分算法(java超详细)
Posted 王水最甜
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二分算法(java超详细)相关的知识,希望对你有一定的参考价值。
文章目录
目录
一、二分查找
1. 整数二分
二分查找:也称折半搜索,对数搜索,是用来在一个有序数组中查找某一元素的算法。
例子:在一个升序数组中查找一个数。每次考察数组当前部分的中间元素(middle),如果中间元素刚好是目标元素(target),就结束搜索。如果中间元素小于所查找的值,就在数组左半部分[left,middle]查找;如果中间元素大于所查找的值,就在数组右半部分[middle,right]查找。
二分搜索法可以用来查找满足某一条件的最大(最小)值。
要求满足某种条件的最大值最小可能情况(最大值最小化),首先的想法是从小到大枚举这个作为答案的[最大值],然后去判断是否合法。若答案单调,就可以使用二分搜索法来更快的找到答案
使用二分搜索法解决[最大值最小化]条件:
-
答案在一个固定区间内
-
比较容易判断某个值是否符合条件
-
可行解对于区间满足一定的单调性(x符合条件,那么x-1或x+1也符合条件)
-
时间复杂度:最优情况O(1),平均/最坏时间复杂度O(log n)
1.1 二分查找算法模板1
算法思路
假设目标值在闭区间[l,r]中,每次将区间长度缩小一半,当l=mid时,找到目标值
区间[l,r]划分为[l,mid-1]和[mid+1,r];更新操作为r=mid-1或l=mid+1。
int binarySearch(int[] nums, int target)
if(nums == null || nums.length == 0) //数组为空
return -1;
int l = 0, r = nums.length - 1; //设置左右边界
while(l <= r)
int mid = l + (r-l) / 2; // 等同于mid=(l+r)/2,这种写法是为了防止数组越界,也可以写为(l+r) >>> 1
if(nums[mid] == target) //最终target=mid,输出mid
return mid;
else if(nums[mid] < target) //目标值在(mid,r]之间
l = mid + 1;
else //目标值在[l,mid)之间
r = mid - 1;
// 最后判断: l>r 即数组不存在
return -1;
1.2 二分查找算法模板2
算法思路
假设目标值在闭区间[l,r]中,每次将区间长度缩小一半,当l=left时,找到目标值
区间[l,r]划分为[l,mid]和[mid+1,r];更新操作为r=mid或l=mid+1(与模板一的区别是界限不同)
int binarySearch(int[] nums, int target)
if(nums == null || nums.length == 0) //数组为空
return -1;
int l = 0, r = nums.length - 1; //设置左右边界
while(l <= r)
int mid = l + (r-l) / 2;
if(nums[mid] > target) //目标值在[l,mid]之间
r = mid;
else if(nums[mid] < target)
l = mid+1;
else
r = mid;
if(nums[l] == target)
return l; //当l=left时,找到目标值的下标
return -1;
1.3 二分查找算法模板3
算法思路
假设目标值在闭区间[l,r]中,每次将区间长度缩小一半,当l=right时,找到目标值
区间[l,r]划分为[l,mid-1]和[mid,r];更新操作为r=mid-1或l=mid(与模板一的区别是界限不同)
int binarySearch(int[] nums, int target)
if(nums == null || nums.length == 0) //数组为空
return -1;
int l = 0, r = nums.length - 1; //设置左右边界
while(l <= r)
int mid = (l+r+1) / 2; //这种版本会有边界问题,计算mid要加1
if(nums[mid] > target) //目标值在[l,mid]之间
r = mid-1;
else if(nums[mid] < target)
l = mid;
else
r=mid-1;
if(nums[r] == target)
return r; //当l=right时,找到目标值的下标
return -1;
1.4 二分查找算法模板4
关于开闭区间问题
二分查找 [left, right)
-
用于查找需要访问数组中当前索引及其直接右邻居索引的元素或条件。
-
使用元素的右邻居来确定是否满足条件,并决定是向左还是向右。
-
保证查找空间在每一步中至少有 2 个元素。
-
需要进行后处理。 当你剩下 1 个元素时,循环 / 递归结束。 需要评估剩余元素是否符合条件。
// 二分查找 [left, right)
int binarySearch2(int[] nums, int target)
if(nums == null || nums.length == 0)
return -1;
// 定义target在左闭右开的区间里,即:[left, right)
int left = 0, right = nums.length;
// 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
while(left < right)
int mid = left + (right - left) / 2;
if(nums[mid] == target)
return mid;
else if(nums[mid] < target)
// target 在右区间,在[mid + 1, right)中
left = mid + 1;
else
// target 在左区间,在[left, middle)中
right = mid;
//当 left == right
if(left != nums.length && nums[left] == target) return left;
return -1;
1.5 二分查找算法模板5
二分查找 (left, right)
搜索需要访问当前索引及其在数组中的直接左右邻居索引的元素或条件。
-
搜索条件需要访问元素的直接左右邻居。
-
使用元素的邻居来确定它是向右还是向左。
-
保证查找空间在每个步骤中至少有 3 个元素。
-
需要进行后处理。 当剩下 2 个元素时,循环 / 递归结束。 需要评估其余元素是否符合条件。
// 二分查找 (left, right)
int binarySearch3(int[] nums, int target)
if (nums == null || nums.length == 0)
return -1;
int left = 0, right = nums.length - 1;
while (left + 1 < right)
int mid = left + (right - left) / 2;
if (nums[mid] == target)
return mid;
else if (nums[mid] < target)
// target 在右区间,在(middle, right)中
left = mid;
else
// target 在左区间,在(left, middle)中
right = mid;
// 当: left + 1 == right
if(nums[left] == target) return left;
if(nums[right] == target) return right;
return -1;
关于模板中出现的边界问题
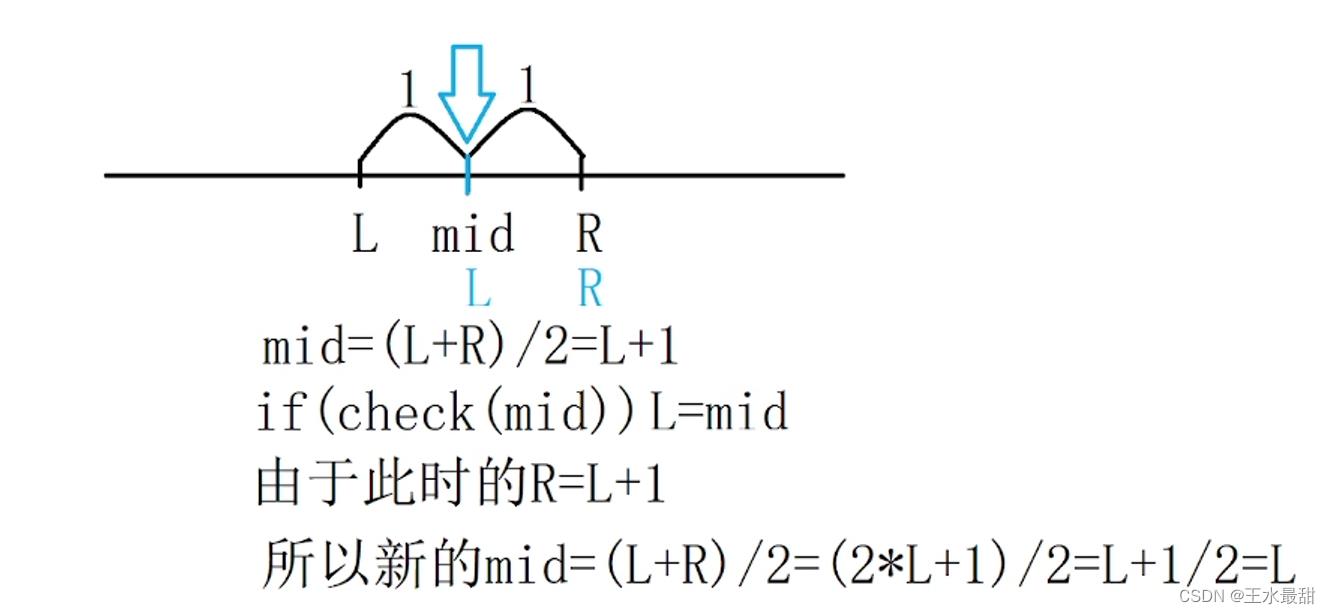
更新之后的mid仍然为L,左右边界没有发生变化,会使while陷入死循环,所以求mid=(r+l+1)/2
练习题目+详解
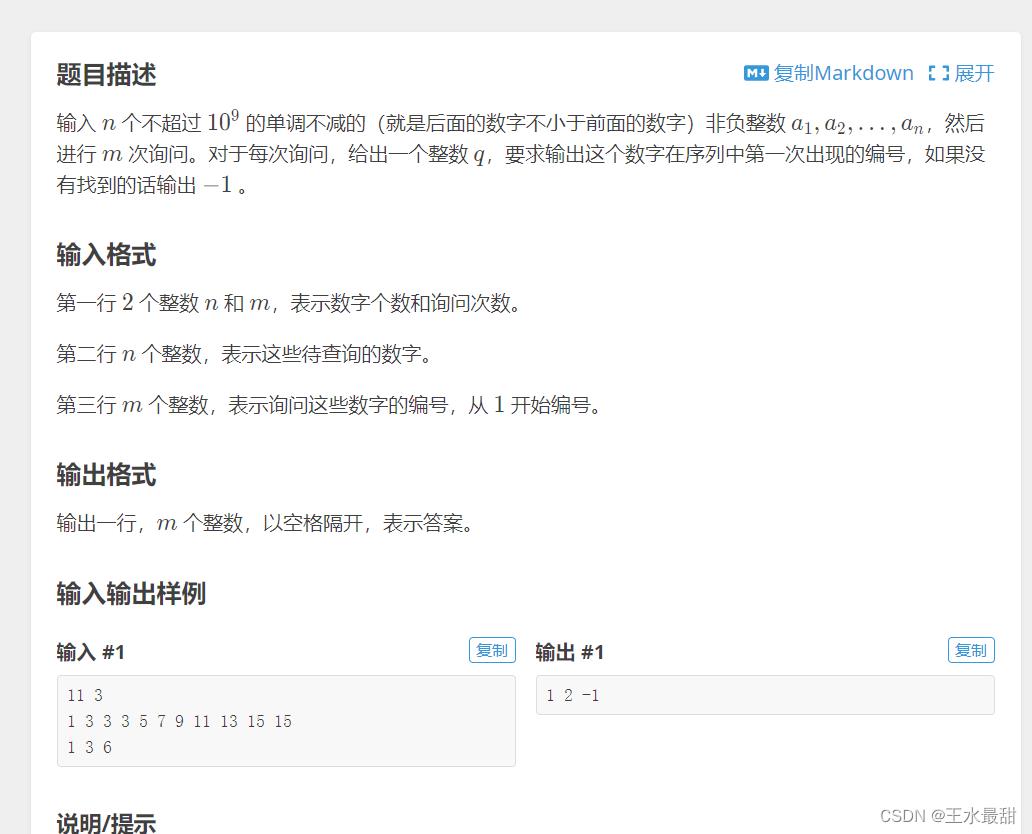
练习题1
思路
思路也很简单,就是用二分法找到每一个数字的下标,这里要注意,我们需要找到每个元素第一次出现的位置,所以需要设置l<r,然后递归的时候r=mid, 这样如果目标值存在的话,就返回l的位置。
代码
public class 二分查找
static int a[] = new int[10^6+10]; //定义一个数组a的全局变量
static int binarySearch(int x, int n) //x是目标值,n是数组长度
int l = 0; int r = n-1 ;
while (l<r)
int mid = (l+r)/2;
if(a[mid] < x) l = mid+1;
else r = mid;
//找到目标值,返回下标
if(a[l] == x) return l+1; //注意:从1开始编号
else return -1;
public static void main(String[] args)
Scanner sc = new Scanner(System.in);
//用户输入n,m 分别代表数组长度,询问次数
int n = sc.nextInt(), m = sc.nextInt();
//这里读入数组
for(int i = 0; i < n; i++)
a[i] = sc.nextInt();
//挨个找数字的下标
for(int i = 0; i < m; i++)
int q = sc.nextInt();
int ans = binarySearch(q, n);
System.out.print(ans + " ");
练习题2
给你一个按照非递减顺序排列的整数数组
nums,和一个目标值target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值target,返回[-1, -1]。你必须设计并实现时间复杂度为O(log n)的算法解决此问题。
思路
直观的思路肯定是从前往后遍历一遍。用两个变量记录第一次和最后一次遇见 target 的下标,但这个方法的时间复杂度为 O(n),没有利用到数组升序排列的条件。由于数组已经排序,因此整个数组是单调递增的,我们可以利用二分法来加速查找的过程。
考虑 target 开始和结束位置,其实我们要找的就是数组中「第一个等于 target 的位置」(记为 left)和「第一个大于 target 的位置减一」(记为 right)。
二分查找中,寻找 left 即为在数组中寻找第一个等于 target 的下标,寻找 right 即为在数组中寻找第一个大于 target 的下标,然后将下标减一。两者的判断条件不同,为了代码的复用,我们定义 searchRange(nums,target) 表示在 nums数组中二分查找 target 的位置 。
最后,因为 target可能不存在数组中,因此我们需要重新校验我们得到的两个下标 left 和 right,看是否符合条件,不符合就返回 -1,-1。
public class 查找下标
public int[] searchRange(int[] nums, int target)
int len = nums.length;
if(len == 0)
return new int[]-1,-1;
int firstPosition = findFirstPosition(nums,target);
if(firstPosition == -1)
return new int[]-1,-1;
int lastPositon = findLastPosition(nums,target);
return new int[]firstPosition,lastPositon;
private int findFirstPosition(int[] nums, int target)
int left = 0;
int right = nums.length-1;
while(left < right) //这里没有包含left=right的情况
int mid = (left+right)/2;
if(nums[mid] < target)
//在[mid+1,right]之间找
left = mid+1;
else if(nums[mid] > target)
//在[ledt,mid-1]之间找
right = mid-1;
else
//在[left,mid]之间找
right = mid;
if(nums[left] == target)
return left;
return -1;
private int findLastPosition(int[] nums, int target)
int left = 0;
int right = nums.length-1;
while(left < right) //这里没有包含left=right的情况
int mid = (left+right+1)/2;
if(nums[mid] < target)
//在[mid+1,right]之间找
left = mid+1;
else if(nums[mid] > target)
//在[ledt,mid-1]之间找
right = mid-1;
else
//在[mid,right]之间找
left = mid;
return left;
- >>表示右移,如果该数为正,则高位补0,若为负数,则高位补1;
- >>>表示无符号右移,也叫逻辑右移,即若该数为正,则高位补0,而若该数为负数,则右移后高位同样补0。
- 时间复杂度:O(log n)
练习题3
整数数组
nums按升序排列,数组中的值 互不相同 。在传递给函数之前,
nums在预先未知的某个下标k(0 <= k < nums.length)上进行了 旋转,使数组变为[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如,[0,1,2,4,5,6,7]在下标3处经旋转后可能变为[4,5,6,7,0,1,2]。给你 旋转后 的数组nums和一个整数target,如果nums中存在这个目标值target,则返回它的下标,否则返回-1。你必须设计一个时间复杂度为
O(log n)的算法解决此问题。
思路
这道题中,数组本身不是有序的,进行旋转后只保证了数组的局部是有序的,这还能进行二分查找吗?答案是可以的。可以发现的是,我们将数组从中间分开成左右两部分的时候,一定有一部分的数组是有序的。拿示例来看,我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分,其中左边 [4, 5, 6] 这个部分的数组是有序的,其他也是如此。这启示我们可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的,并根据有序的那个部分确定我们该如何改变二分查找的上下界,因为我们能够根据有序的那部分判断出 target 在不在这个部分:
-
如果
[l, mid - 1]是有序数组,且 target 的大小满足[nums[l],nums[mid],则我们应该将搜索范围缩小至[l, mid - 1],否则在[mid + 1, r]中寻找。 -
如果
[mid, r]是有序数组,且 target 的大小满足[nums[mid+1],nums[r]],则我们应该将搜索范围缩小至[mid + 1, r],否则在[l, mid - 1]中寻找。
需要注意的是,二分的写法有很多种,所以在判断 target 大小与有序部分的关系的时候可能会出现细节上的差别。
public class 螺旋数组
public int search(int[] nums, int target)
int n = nums.length;
if (n == 0)
return -1;
if (n == 1)
return nums[0] == target ? 0 : -1;
int l = 0, r = n - 1;
while (l <= r)
int mid = (l + r) / 2;
if (nums[mid] == target)
return mid;
if (nums[0] <= nums[mid]) //如果左边是有序的
if (nums[0] <= target && target < nums[mid]) //目标值在左边
r = mid - 1;
else //如果目标值在右边
l = mid + 1;
else //如果左边是无序的,就相当于遍历该区间元素了
if (nums[mid] < target && target <= nums[n - 1]) //目标值在右边
l = mid + 1;
else
r = mid - 1;
return -1;
复杂度分析
-
时间复杂度: O(logn),其中 n 为nums 数组的大小。整个算法时间复杂度即为二分查找的时间复杂度 O(logn)。
-
空间复杂度: O(1) 。我们只需要常数级别的空间存放变量。
2. 浮点数二分
浮点数二分:将整数二分中的mid的类型替换成double,将区间更新操作改为l=mid或r=mid,当区间长度足够小(能求出答案时),就可以结束二分。注:浮点数二分不存在边界问题。
代码示例
double binarySearch(int[] nums,int target)
// eps 表示精度,取决于题目对精度的要求
double l = 0; double r = nums.length-1;
const double eps = 1e-6; //科学计数法1*10^-6 当区间长度小于eps时退出循环
while (r - l > eps) //当区间长度大于eps时继续二分
double mid = (l + r) / 2;
if (nums[mid] > target ) r = mid;
else l = mid;
return l; //最后while循环退出的时候l和r近似相等
总结
这里对文章进行总结:
以上就是整理的二分算法的内容,本文仅仅简单介绍了二分算法,而要在具体的题目中真正掌握运用二分算法,还需要多加练习二分算法的各种题目。
❤️数据结构和算法动图演示,超详细,就怕你不会!二分查找详解建议收藏❤️
🎈 作者:Linux猿
🎈 简介:CSDN博客专家🏆,华为云享专家🏆,Linux、C/C++、面试、刷题、算法尽管咨询我,关注我,有问题私聊!
🎈 关注专栏:图解数据结构和算法(优质好文持续更新中……)🚀
🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬
目录
在数据结构和算法的学习中,需要查找数据时,经常使用到二分查找算法,下面就来详细讲解下二分查找的各种用法。
🍓一、什么是二分查找算法 ?
二分查找算法是在有序序列中查找某一特定元素的查找算法,所谓 “二分”,即:每次查找可以排除一半的元素,所以时间复杂度为 O(log2^n),因此也被称为折半查找(指的是对半排除元素),对数查找(对数指的时间复杂度中的对数)。
________🐌 我是分割线 🐢________
🍓二、二分查找算法
🚩2.1 普通二分查找
⭐2.1.1 算法步骤
假设存在长度为 n 的 升序 数组 A[],查找元素 target 是否存在。
注意:数组降序也是可以的,二分查找一般情况下是升序或降序,符合特定规则的升序和降序也是可以的,比如:两段升序的拼接,这里以升序为例进行讲解。
(0)首先,初始化 left = 0, right = n,表示查找的区间为 [ left,right),最开始时,查找的区间为 [0, n);
(1)计算 left 和 right 的中间节点,中间节点的下标为 mid = (left + right) /2 。
(2)然后,判断 target 与 中间节点值 A[ mid ] 的大小;
(3)如果 target = A[ mid ] ,说明在数组 A 中找到了元素 target,结束查询;
(4)如果 target < A [ mid ] ,说明,target 并不在数组 A 的区间 [mid, right) 中,因为数组 A 是升序数组,所以 target 应该在区间 [left,mid) 中,所以 left 值不变,让 right = mid;
(5)否则,target > A[ mid ],说明,target 在区间 [ mid + 1,right) 中,同样,是因为数组 A 是升序数组,所以 right 的值不变,让 left = mid + 1;
(6)重复步骤 (1)~(5),直到查找到 target 或 left >= right 为止,如果出现 left >= right(这时区间为空,没有元素了),则表示数组 A 中没有找到 target 。
⭐2.1.2 动图演示
来看一下动图演示,假设升序数组 A[] = {1, 3, 5, 7, 9, 11, 13},查找 target = 1,如下所示:

在上述动图中,一共查找了三次,第三次 mid = 0,便查找到了 target = 1,具体查找步骤如下所示:
(1)、最开始查找范围为 [0, 7),left = 0, right = 7, 计算 mid = 3;
(2)、缩小查找范围为 left = 0, right = 3,查找范围为 [ 0, 3),重新计算 mid = 1;
(3)、再次缩小查找范围 left = 0, right = 1,查找范围为 [0, 1),重新计算 mid = 0;
(4)、A[ mid = 0 ] = 1 ,查找到 target。
上述就是二分查找数组 A 中 1 的过程。
⭐2.1.3 代码实现
/*
A[] : 升序数组,假设要排序的元素为n个
left : 排序数组的左边的值,初始为 0
right : 排序数组的右边的值,初始为 n,切记不是n-1
target : 要查找的值
*/
int binarySearch(int A[], int n, int target){
int left = 0, right = n;
while(left < right){ // 查找的区间为 [left, right)
int mid = (left + right) / 2; // 更好的方法是:mid = left + (right - left) / 2 能防止溢出
if(A[mid] == target) return mid;
else if(A[mid] > target) right = mid;
else left = mid + 1;
}
return -1; // 查找不到
}在计算 mid 的时候,可以使用如下方式:
mid = left + (right - left) / 2能够方式 left + right 的溢出。
🚩2.2 二分查找下界
⭐2.2.1 算法步骤
假设存在长度为 n 的 升序 数组 A[],数组中存在重复的元素,要查找元素 target 的最小下标。如下所示:

(0)首先,初始化 left = 0, right = n,表示查找的区间为 [ left,right),最开始时,查找的区间为 [0, n);
(1)计算 left 和 right 的中间节点,中间节点的下标为 mid = (left + right) /2 。
(2)然后,判断 target 与 中间节点值 A[ mid ] 的大小;
(3)如果 A[ mid ] >= target,因为查找的是下界,所以 target 在区间 [ left, mid) 区间还可能存在,所以进一步缩小空间,将查找区间缩小为 [left, mid),所以 left 值不变,让 right = mid;
(4)否则,A[ mid ] < target,说明 target 在区间 [ mid + 1,right) 中,因为数组 A 是升序数组,所以 right 的值不变,让 left = mid + 1;
(5)重复步骤 (1)~(4),直到跳出 while 循环;
(6)如果 right 等于 n 或 A [ right ] != target ,则表示未查找到 target,否则 A[ right ] = target,right 为数组 A 中值为 target 的最小下标;
⭐2.2.2 动图演示
来看一下动图演示,假设升序数组 A[] = {1, 3, 3, 3, 9, 11, 13},查找 target = 3,如下所示:

在上述动图中,一共查找了三次,第三次 mid = 0 结束查找(代码中是 left == right 跳出 while 循环)right 指向的值等于 target,具体查找步骤如下所示:
(1)、最开始查找范围为 [0, 7),left = 0, right = 7, 计算 mid = 3;
(2)、因为[0, 3) 中可能还存在 target,缩小查找范围为 left = 0, right = 3,新查找范围为 [ 0, 3),重新计算 mid = 1;
(3)、因为[0, 1) 中可能还存在 target,再次缩小查找范围 left = 0, right = 1,新查找范围为 [0, 1),重新计算 mid = 0;
(4)、left 重新计算后,left == right,结束查找,right 指向的值等于 target。
上述就是二分查找数组 A 中 3 的最小下标的过程。
⭐2.2.3 代码实现
/*
A[] : 升序数组,假设要排序的元素为 n 个
left : 查找区间的最左边的下标,初始为 0
right : 查找区间的最右边的下标,初始为 n
target: 要查找的值
*/
int lowerSearch(int A[], int n, int target){
int left = 0, right = n;
while(left < right){
int mid = left + (right - left)/2;
if(A[mid] >= target) right = mid;
else left = mid + 1;
}
if(right == n || A[right] != target)
return -1;
return right;
}注意:需要判断 right 是否是指向 target,因为查找数组中可能就不存在 target。
🚩2.3 二分查找上界
⭐2.2.1 算法步骤
假设存在长度为 n 的 升序 数组 A[],数组中存在重复的元素,要查找元素 target 的最大下标。如下所示:

(0)首先,初始化 left = 0, right = n,表示查找的区间为 [ left,right),最开始时,查找的区间为 [0, n);
(1)计算 left 和 right 的中间节点,中间节点的下标为 mid = (left + right) /2 。
(2)然后,判断 target 与 中间节点值 A[ mid ] 的大小;
(3)如果 A[mid] > target,所以 target 在区间 [ left,mid) 中,所以缩小空间,将查找区间缩小为 [left, mid),所以 left 值不变,让 right = mid;
(4)否则,A[ mid ] <= target,说明 target 在区间 [ mid + 1,right) 中还可能存在,因为数组 A 是升序数组,所以 right 的值不变,让 left = mid + 1;
(5)重复步骤 (1)~(4),直到跳出 while 循环,left --,因为 left 指向的永远是比 target 大的值的下标;
(6)如果新的 left 等于 n 或 A [ left ] != target ,则表示未查找到 target,否则 A[ left ] = target,right 为数组 A 中值为 target 的最小下标;
⭐2.2.2 动图演示
来看一下动图演示,假设升序数组 A[] = {1, 3, 3, 3, 9, 11, 13},查找 target = 3,如下所示:

在上述动图中,一共查找了三次,第三次 mid = 4 结束查找(代码中是 left == right 跳出 while 循环)left - 1 指向的值等于 target,具体查找步骤如下所示:
(1)、最开始查找范围为 [0, 7),left = 0, right = 7, 计算 mid = 3;
(2)、因为[4, 7) 中可能还存在 target,缩小查找范围为 left = 4, right = 7,新查找范围为 [ 4, 7),重新计算 mid = 5;
(3)、因为[4, 5) 中可能还存在 target,再次缩小查找范围 left = 4, right = 5,新查找范围为 [4, 5),重新计算 mid = 4;
(4)、left 重新计算后,left == right,结束查找,left - 1 指向的值等于 target。
上述就是二分查找数组 A 中 3 的最大下标的过程。
⭐2.2.3 代码实现
/*
A[] : 升序数组,假设要排序的元素为 n 个
left : 查找区间的最左边的下标,初始为 0
right : 查找区间的最右边的下标,初始为 n
target: 要查找的值
*/
int upperSearch(int A[], int n, int target){
int left = 0, right = n;
while(left < right){
int mid = left + (right - left)/2;
if(A[mid] > target) right = mid;
else left = mid + 1;
}
left--;
if(left == n || A[left] != target)
return -1;
return left;
}这里需要注意,left 是查找值更大值的下标,所以让 left --,还需要判断一下 left 所指向的值是否是 target,因为可能在查找数组中就不存在 target。
________🐌 我是分割线 🐢________
🍓三、STL 中的二分查找函数
🚩3.0 头文件
使用 STL 中的二分查找函数,需要引入如下头文件:
#include <algorithm>🚩3.1 普通二分查找
⭐3.1.1 函数介绍
函数如下所示:
binary_search(A, A + n, target)其中:
binary_search : 函数名;
A : 查找的数组;
n : 数组 A 的长度;
target : 查找的目标值
⭐3.1.2 代码示例
#include <iostream>
#include <algorithm> // 头文件
using namespace std;
int main()
{
int n = 8;
int A[] = {1, 3, 5, 7, 9, 11, 13, 15};
cout<<binary_search(A, A + n, 9)<<endl;
return 0;
}上述代码中,查找数组 A 中是否存在 9,输出结果为 1。
🚩3.2 二分查找下界
⭐3.2.1 函数介绍
函数如下所示:
lower_bound(A, A + n, 3) 其中:
lower_bound : 函数名;
A : 查找的数组;
n : 数组 A 的长度;
target : 查找的目标值;
注意:函数 lower_bound 返回的是数组目标值最小下标的地址,想要计算下标,需要减去数组 A 的首地址。
⭐3.2.2 代码示例
#include <iostream>
#include <algorithm> // 头文件
using namespace std;
int main()
{
int n = 8;
int A[] = {1, 3, 3, 3, 9, 11, 13, 15};
cout<<lower_bound(A, A + n, 3) - A<<endl;
return 0;
}如上所示,计算下标值需要减去数组 A 的首地址,输出为 1。
🚩3.3 二分查找上界
⭐3.3.1 函数介绍
函数如下所示:
upper_bound(A, A + n, 3) 其中:
lower_bound : 函数名;
A : 查找的数组;
n : 数组 A 的长度;
target : 查找的目标值;
注意:函数 upper_bound 返回的是数组目标值第一个大于目标值的地址,想要计算下标,需要减去数组 A 的首地址。
⭐3.3.2 代码示例
#include <iostream>
#include <algorithm> // 头文件
using namespace std;
int main()
{
int n = 8;
int A[] = {1, 3, 3, 3, 9, 11, 13, 15};
cout<<upper_bound(A, A + n, 3) - A<<endl;
return 0;
}注意:上述返回的是大于目标值的第一个元素的下标,输出为 4。
________🐌 我是分割线 🐢________
🍓四、复杂度分析
🚩4.1 时间复杂度
每次查找都是排除一半的情况(缩减一半),相当于每次都除以 2,假设长度为 n,查找次数为 x,则 2^x <= n ,x 约等于 log2^n,所以时间复杂度为 O(log2^n)。
🚩4.2 空间复杂度
通常二分查找并不需要额外的辅助空间,所以空间复杂度为 O(1)。
________🐌 我是分割线 🐢________
🍓五、总结
最长使用的还是普通的二分查找算法,特殊情况会查找上界或下界,当然,可以使用 STL 中的库函数。
欢迎关注下方👇👇👇公众号👇👇👇,获取更多优质内容🤞(比心)!
以上是关于二分算法(java超详细)的主要内容,如果未能解决你的问题,请参考以下文章