2023-4-1刷提情况

Posted 2023-04-03 MoYu1419

[蓝桥杯 2022 省 B] 积木画

题目描述

小明最近迷上了积木画，有这么两种类型的积木，分别为 $I$ 型（大小为 $2$ 个单位面积) 和 $L$ 型 (大小为 $3$ 个单位面积):

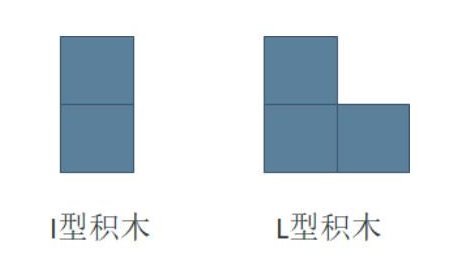
同时，小明有一块面积大小为 $2\times N$ 的画布，画布由 $2\times N$ 个 $1\times 1$ 区域构成。小明需要用以上两种积木将画布拼满，他想知道总共有多少种不同的方式? 积木可以任意旋转，且画布的方向固定。

输入格式

输入一个整数 $N$，表示画布大小。

输出格式

输出一个整数表示答案。由于答案可能很大，所以输出其对 $1000000007$（即 $10^9+7$）取模后的值。

样例 #1

样例输入 #1

3

样例输出 #1

5

提示

【样例说明】

五种情况如下图所示, 颜色只是为了标识不同的积木:

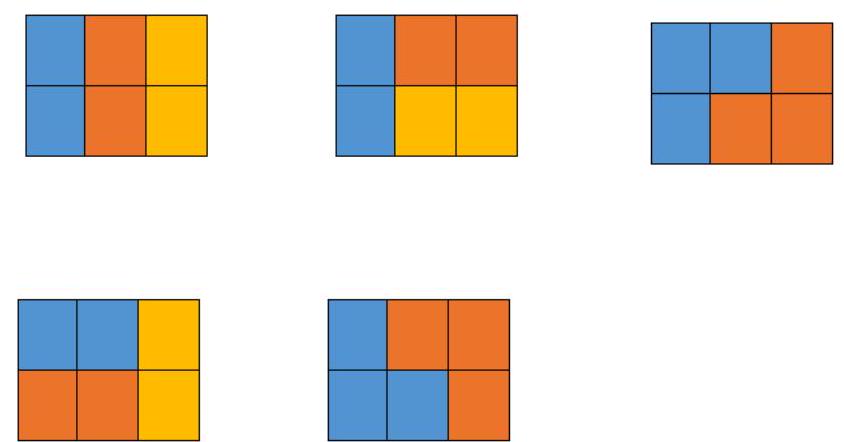
【评测用例规模与约定】

对于所有测试用例，$1\le N\le 10^7$。

蓝桥杯 2022 省赛 B 组 G 题。

思路

dp题目:
dp[i][0] 代表当前填满方块的方案数
dp[i][1] 代表当前只有上面一个方块的方案数
dp[i][2] 代表当前只有下面一个方块的方案数
那么状态转移方程为：
dp[i][0] = dp[i-1][0] + dp[i-2][0] + dp[i-1][1] + dp[i-1][2]
dp[i][1] = dp[i-1][2] + dp[i-2][0];
dp[i][2] = dp[i-1][1] + dp[i-1][0];

代码实现

#include<bits/stdc++.h>

using namespace std;

const int mod = 1e9 + 7;
int n, f[10000005][3];

int main()
    cin >> n;
    if(n == 1)
        cout << 1 << endl;
        return 0;
    
    f[0][0] = 1;
    f[1][0] = 1;
    for(int i = 2; i <= n; i++)
        f[i][0] = ((f[i-1][0] + f[i-2][0]) % mod + (f[i-1][1] + f[i-1][2]) % mod) % mod;
        f[i][1] = (f[i-1][2] + f[i-2][0]) % mod;
        f[i][2] = (f[i-1][1] + f[i-2][0]) % mod;
     
    cout << f[n][0] << endl;
    return 0;

刷提总结——火柴排队（NOIP2013）

题目：

题目背景

NOIP2013 提高组 Day1 试题

题目描述

涵涵有两盒火柴，每盒装有 n 根火柴，每根火柴都有一个高度。现在将每盒中的火柴各自排成一列，同一列火柴的高度互不相同，两列火柴之间的距离定义为：

其中 ai 表示第一列火柴中第 i个火柴的高度，bi 表示第二列火柴中第 i 个火柴的高度。 

每列火柴中相邻两根火柴的位置都可以交换，请你通过交换使得两列火柴之间的距离最小。请问得到这个最小的距离，最少需要交换多少次？如果这个数字太大，请输出这个最小交换次数对 99,999,997 取模的结果。 

输入格式

共三行，第一行包含一个整数 n，表示每盒中火柴的数目。 
第二行有 n 个整数，每两个整数之间用一个空格隔开，表示第一列火柴的高度。 
第三行有 n 个整数，每两个整数之间用一个空格隔开，表示第二列火柴的高度。 

输出格式

输出共一行，包含一个整数，表示最少交换次数对 99,999,997 取模的结果。

样例数据 1

输入　 [复制]

 

 

4 
2 3 1 4 
3 2 1 4

输出

1

样例数据 2

输入　 [复制]

 

 

4 
1 3 4 2 
1 7 2 4

输出

2

备注

【样例1说明】 
最小距离是 0，最少需要交换 1 次，比如：交换第 1 列的前 2 根火柴或者交换第 2 列的前 2 根火柴。

【样例2说明】 
最小距离是 10，最少需要交换 2 次，比如：交换第 1 列的中间 2 根火柴的位置，再交换第 2 列中后 2 根火柴的位置。 

【数据范围】 
对于 10% 的数据， 1≤n≤10； 
对于 30% 的数据，1≤n≤100； 
对于 60% 的数据，1≤n≤1,000；
对于 100% 的数据，1≤n≤100,000 ；0≤火柴高度≤231-1

题解:

这里引用ssoj官网题解：

贪心+逆序对。分析如下：

对距离公式化简得：

∑(ai-bi)2=∑(ai2-2aibi+bi2)=∑ai2+∑bi2-2∑aibi，要求∑(ai-bi)2最小，就只需要∑aibi最大即可。这里有个贪心，当 a1<a2<…<an ，b1<b2<…<bn时，∑aibi最大。

证明如下：

若存在a>b，c>d，且ac+bd<ad+bc，则a(c-d)<b(c-d)，则a<b，与a>b矛盾，所以若a>b，c>d，则ac+bd>ad+bc
将此式子进行推广：
当a1<a2<a3<…<an ，b1<b2<…<bn的情况下∑aibi最大，即∑(ai-bi)2最小。

然后，将两个序列分别排序，确定每对数的对应关系，明显，同时移动两个序列中的数等效于只移动一个序列中的数，移动的时候可以将一个火柴序列不动，只移动另外一个序列。

于是可以构造一个数组C，C[i]表示最初的第i个数应该移动到C[i]位置。于是问题转换成对C[i]数组排序，每次可以交换相邻两个数，问最少需要移动多少次的问题了，也就是求这个序列的逆序对数量的问题（这里用归并排序思想实现）。

例如：
对于数据：
4
1 3 4 2
1 7 2 4

先排序:
1 2 3 4
1 2 4 7

 

保持序列1不动，那么：
序列2中的“1”对应序列1中的位置1；
         “7”对应序列1中的位置3；
         “2”对应序列1中的位置4；
         “4”对应序列1中的位置2，那么重定义数组c为：

这个序列：1 3 4 2 的逆序对数量是 2 ，即（3,2）和(4,2)，所以答案是 2。

md其实两个数组排序的位置一一对应时最小都已经想到了····那个逆序对竟然想不到···哎·····

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int N=1e5+5;
const int mod=99999997;
int n,c[N],temp[N];
long long ans=0;
struct node
{
  int w;
  int id;
}a[N],b[N];
int R()
{
  int f=0;
  char c;
  for(c=getchar();c<‘0‘||c>‘9‘;c=getchar());
  for(;c<=‘9‘&&c>=‘0‘;c=getchar())
    f=(f<<3)+(f<<1)+c-‘0‘;
  return f;
}
bool comp(node x,node y)
{
  return x.w<y.w;
}
inline void merge(int x,int mid,int y)
{
  int i=x,j=mid+1,head=x;  
  while(i<=mid&&j<=y)
  {
    if(c[i]<=c[j])
      temp[head++]=c[i++];
    else
    {
      ans=(ans+mid-i+1)%mod;
      temp[head++]=c[j++];
    }
  }
  while(i<=mid)  temp[head++]=c[i++];
  while(j<=y)  temp[head++]=c[j++];
  for(i=x;i<=y;i++) 
    c[i]=temp[i];
}
inline void mergesort(int a,int b)
{
  if(a==b)  return;
  int mid=(a+b)/2;
  mergesort(a,mid);
  mergesort(mid+1,b);
  merge(a,mid,b);
}
int main()
{
  //freopen("a.in","r",stdin);
  n=R();
  for(int i=1;i<=n;i++)
  {  
    a[i].w=R();
    a[i].id=i;
  }
  for(int i=1;i<=n;i++)
  {    
    b[i].w=R();
    b[i].id=i;
  }
  sort(a+1,a+n+1,comp);
  sort(b+1,b+n+1,comp);
  for(int i=1;i<=n;i++)
    c[b[i].id]=a[i].id;
  mergesort(1,n);
  cout<<ans<<endl;
  return 0;
}