开始使用 Transformer 模型的架构

Posted 2023-04-02 Sonhhxg_柒

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了开始使用 Transformer 模型的架构相关的知识，希望对你有一定的参考价值。

🔎大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流🔎

📝个人主页－Sonhhxg_柒的博客_CSDN博客 📃

🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝

📣系列专栏 - 机器学习【ML】自然语言处理【NLP】深度学习【DL】

🖍foreword

✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

如果你对这个系列感兴趣的话，可以关注订阅哟👋

语言是人类交流的本质。如果没有构成语言的词序列，文明就不会诞生。我们现在大多生活在语言数字表示的世界中。我们的日常生活依赖于 NLP 数字化语言功能：网络搜索引擎、电子邮件、社交网络、帖子、推文、智能手机短信、翻译、网页、流媒体网站上的语音到文本的转录、热线服务上的文本到语音，以及更多日常功能。

第 1 章，什么是变形金刚？，解释了 RNN 的局限性以及云 AI 转换器的诞生，接管了相当一部分的设计和开发。工业 4.0 开发人员的角色是了解原始 Transformer 的架构以及随后的多个 Transformer 生态系统。

2017 年 12 月，Google Brain 和 Google Research 发表了开创性的Vaswani等人，Attention is All You Need论文。变形金刚诞生了。Transformer 的性能优于现有的最先进的 NLP 模型。Transformer 的训练速度比以前的架构更快，并获得了更高的评估结果。因此，Transformer 已成为 NLP 的关键组成部分。

Transformer 的注意力头的想法是取消递归神经网络特征。在本章中，我们将揭开Vaswani等人描述的 Transformer 模型的面纱。（2017）并检查其架构的主要组成部分。我们将探索迷人的注意力世界，并说明 Transformer 的关键组件。

本章涵盖以下主题：

Transformer的架构
Transformer 的自注意力模型
编码和解码堆栈
输入和输出嵌入
位置嵌入
自注意力
多头注意力
掩码多注意力
残剩连接
标准化
前馈网络
输出概率

让我们直接深入了解原始 Transformer 架构的结构。

Transformer的崛起：注意力就是你所需要的

2017 年 12 月，Vaswani等人。(2017) 发表了他们的开创性论文，Attention is All You Need。他们表演他们在 Google Research 和 Google Brain 的工作。在本章和本书中，我将把Attention is All You Need中描述的模型称为“原始 Transformer 模型”。

附录 I，Transformer Models 的术语，可以帮助从深度学习单词的经典用法过渡到 Transformer 词汇表。附录 I总结了神经网络模型的经典 AI 定义的一些变化。

在本节中，我们将看看他们构建的 Transformer 模型的结构。在以下部分中，我们将探讨模型的每个组件内部的内容。

原始的 Transformer 模型是 6 层的堆栈。第l层的输出是第l +1层的输入，直到达到最终预测。左侧有 6 层编码器堆栈，右侧有 6 层解码器堆栈：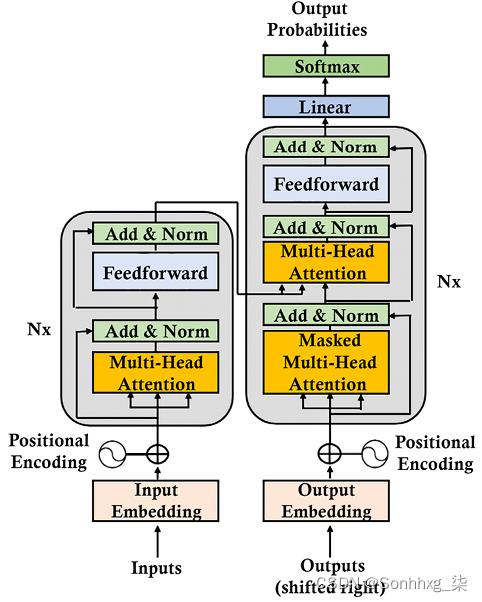

图 2.1：Transformer 的架构

在左侧，输入通过注意力子层和前馈子层进入Transformer的编码器端。在右侧，目标输出通过两个注意力子层和一个前馈网络子层进入 Transformer 的解码器端。我们立即注意到没有 RNN、LSTM 或 CNN。在这个架构中已经放弃了重复。

随着两个词之间距离的增加，注意力已经取代了需要增加参数的递归函数。注意机制是一种“逐字逐句”的操作。它实际上是一个token到token的操作，但是我们将它保持在单词级别以保持解释的简单。注意力机制将发现每个单词如何与序列中的所有其他单词相关，包括正在分析的单词本身。让我们检查以下序列：

The cat sat on the mat.

注意会在词向量之间运行点积并确定一个词与所有其他词的最强关系，包括它自己（“cat”和“cat”）：

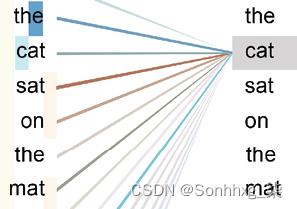
图 2.2：注意所有单词

注意力机制将提供更深层次的词之间的关系并产生更好的结果。

对于每个注意力子层，原始的 Transformer 模型并行运行不是一个而是八个注意力机制来加速计算。我们将在下一部分编码器堆栈中探索这种架构。这个过程被命名为“多头注意”，提供：

对序列进行更广泛的深入分析
排除递归减少计算操作
并行化的实现，减少了训练时间
每个注意力机制学习相同输入序列的不同视角

注意更换复发。但是，Transformer 还有其他几个创造性方面，它们与注意力机制一样重要，当我们查看架构内部时您会看到。

我们只是从外部查看了 Transformer 结构。现在让我们进入 Transformer 的每个组件。我们将从编码器开始。

编码器堆栈（The encoder stack）

的层数原Transformer的编码器和解码器模型是层堆叠。编码器堆栈的每一层具有以下结构：

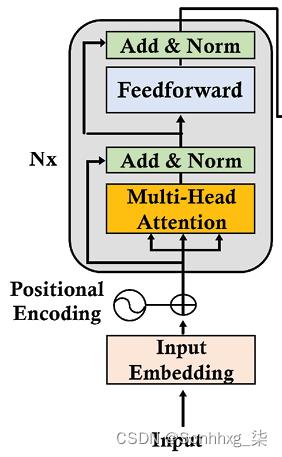
图 2.3：Transformer 的编码器堆栈的一层

对于 Transformer 模型的所有N = 6 层，原始编码器层结构保持不变。每层包含两个主要子层：多头注意力机制和完全连接的位置前馈网络。

请注意，Transformer 模型中的每个主要子层sublayer ( x ) 周围都有一个残差连接。这些连接将子层的未处理输入x传输到层归一化函数。这样，我们可以确定位置编码等关键信息不会在途中丢失。因此，每一层的归一化输出为：

LayerNormalization (x + Sublayer(x))

尽管编码器的N = 6 层中的每一层的结构都是相同的，但每一层的内容与前一层并不严格相同。

例如，嵌入子层仅存在于堆栈的底层。其他五层不包含嵌入层，这保证了编码输入在所有层中都是稳定的。

此外，多头注意力机制从第 1 层到第 6 层执行相同的功能。但是，它们执行的任务不同。每一层都从前一层学习，并探索在序列中关联标记的不同方式。它寻找各种单词的关联，就像我们在解决填字游戏时寻找字母和单词的不同关联一样。

的设计者Transformer 引入了一个非常有效的约束。模型的每个子层的输出都有一个恒定的维度，包括嵌入层和残差连接。该维度是d模型，可以根据您的目标设置为另一个值。在原始的 Transformer 架构中，dmodel = 512.。

d模型具有强大的后果。实际上所有的关键操作都是点积。结果，维度保持稳定，这减少了计算的操作次数，减少了机器消耗，并且更容易在信息流经模型时对其进行跟踪。

编码器的这个全局视图显示了 Transformer 高度优化的架构。在以下部分中，我们将放大每个子层和机制。

我们将从嵌入子层开始。

输入嵌入（Input embedding）

输入嵌入子层转换输入使用原始 Transformer 模型中的学习嵌入标记到维度d model = 512 的向量。输入嵌入的结构是经典的：

图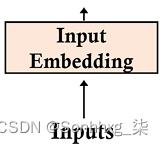

2.4：Transformer 的输入嵌入子层

嵌入子层的工作方式与其他标准转导模型类似。标记器将句子转换为标记。每个分词器都有自己的方法，例如 BPE、单词片段和句子片段方法。Transformer 最初使用 BPE，但其他模型使用其他方法。

目标是相似的，选择取决于所选择的策略。例如，应用于序列的标记器the Transformer is an innovative NLP model!将在一种模型中生成以下标记：

['the', 'transform', 'er', 'is', 'an', 'innovative', 'n', 'l', 'p', 'model', '!']

你会请注意，此标记器对字符串进行了规范化小写并将其截断为子部分。分词器通常会提供一个整数表示，用于嵌入过程。例如：

text = "The cat slept on the couch.It was too tired to get up."
tokenized text= [1996, 4937, 7771, 2006, 1996, 6411, 1012, 2009, 2001, 2205, 5458, 2000, 2131, 2039, 1012]

此时标记化文本中没有足够的信息来进一步研究。必须嵌入标记化的文本。

Transformer 包含一个学习的嵌入子层。许多嵌入方法可以应用于标记化输入。

word2vec我选择了谷歌在 2013 年提供的嵌入方法的 skip-gram 架构来说明 Transformer 的嵌入子层。skip-gram 将专注于单词窗口中的中心单词并预测上下文单词。例如，如果 word(i) 是两步窗口中的中心词，skip-gram 模型将分析 word(i-2)、word(i-1)、word(i+1) 和 word( i+2)。然后窗口将滑动并重复该过程。skip-gram 模型通常包含输入层、权重、隐藏层和包含标记化输入词的词嵌入的输出。

假设我们需要对以下句子进行嵌入：

The black cat sat on the couch and the brown dog slept on the rug.

我们将专注于两个词，black和brown。这两个词的词嵌入向量应该是相似的。

由于我们必须为每个单词生成一个大小为d model = 512 的向量，我们将为每个单词获得一个大小512向量嵌入：

black=[[-0.01206071  0.11632373  0.06206119  0.01403395  0.09541149  0.10695464 0.02560172  0.00185677 -0.04284821  0.06146432  0.09466285  0.04642421 0.08680347  0.05684567 -0.00717266 -0.03163519  0.03292002 -0.11397766 0.01304929  0.01964396  0.01902409  0.02831945  0.05870414  0.03390711 -0.06204525  0.06173197 -0.08613958 -0.04654748  0.02728105 -0.07830904
    …
0.04340003 -0.13192849 -0.00945092 -0.00835463 -0.06487109  0.05862355 -0.03407936 -0.00059001 -0.01640179  0.04123065 
-0.04756588  0.08812257 0.00200338 -0.0931043  -0.03507337  0.02153351 -0.02621627 -0.02492662 -0.05771535 -0.01164199 
-0.03879078 -0.05506947  0.01693138 -0.04124579 -0.03779858 
-0.01950983 -0.05398201  0.07582296  0.00038318 -0.04639162 
-0.06819214  0.01366171  0.01411388  0.00853774  0.02183574 
-0.03016279 -0.03184025 -0.04273562]]

这个词black现在由512维度表示。可以使用其他嵌入方法，并且dmodel可以具有更多的维度。

的词嵌入brown也用512维度表示：

brown=[[ 1.35794589e-02 -2.18823571e-02  1.34526128e-02  6.74355254e-02
   1.04376070e-01  1.09921647e-02 -5.46298288e-02 -1.18385479e-02
   4.41223830e-02 -1.84863899e-02 -6.84073642e-02  3.21860164e-02
   4.09143828e-02 -2.74433400e-02 -2.47369967e-02  7.74542615e-02
   9.80964210e-03  2.94299088e-02  2.93895267e-02 -3.29437815e-02
…
  7.20389187e-02  1.57317147e-02 -3.10291946e-02 -5.51304631e-02
  -7.03861639e-02  7.40829483e-02  1.04319192e-02 -2.01565702e-03
   2.43322570e-02  1.92969330e-02  2.57341694e-02 -1.13280728e-01
   8.45847875e-02  4.90090018e-03  5.33546880e-02 -2.31553353e-02
   3.87288055e-05  3.31782512e-02 -4.00604047e-02 -1.02028981e-01
   3.49597558e-02 -1.71501152e-02  3.55573371e-02 -1.77437533e-02
  -5.94457164e-02  2.21221056e-02  9.73121971e-02 -4.90022525e-02]]

为了验证为这两个词生成的词嵌入，我们可以使用余弦相似度来查看词的词嵌入black和brown是否相似。

余弦相似性使用欧几里得 (L2) 范数在单位球体中创建向量。我们正在比较的向量的点积是之间的余弦这两个向量的点。有关余弦相似性理论的更多信息，您可以查阅 scikit-learn 的文档，其中许多其他来源：https ://scikit-learn.org/stable/modules/metrics.html#cosine-similarity 。

在示例的嵌入中，大小为d model = 512 的黑色向量与大小为d model = 512 的棕色向量之间的余弦相似度为：

cosine_similarity(black, brown)= [[0.9998901]]

skip-gram 产生了两个彼此接近的向量。它检测到黑色和棕色构成了词典的颜色子集。

Transformer 的后续层不会空手而归。他们学习了已经提供了有关如何关联单词的信息的词嵌入。

但是，由于没有额外的向量或信息指示单词在序列中的位置，因此丢失了大量信息。

Transformer 的设计者提出了另一个创新功能：位置编码。

让我们看看位置编码是如何工作的。

位置编码（Positional encoding）

我们进入Transformer 的这个位置编码函数不知道单词在序列中的位置：

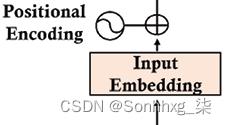
图 2.5：位置编码

我们不能创建独立的位置向量，这会对 Transformer 的训练速度造成高成本，并使注意力子层的使用过于复杂。这个想法是向输入嵌入添加位置编码值，而不是使用额外的向量来描述序列中标记的位置。

工业 4.0 务实且与模型无关。原始的 Transformer 模型只有一个包含词嵌入和位置编码的向量。我们将在第 15 章“从 NLP 到与任务无关的 Transformer 模型”中使用单独的位置编码矩阵来探索解开注意力。

Transformer 期望位置编码函数输出的每个向量都有一个固定大小的d model = 512（或模型的其他常数值）。

如果我们回到我们在词嵌入子层中使用的句子，我们可以看到黑色和棕色在语义上可能相似，但它们在句子中相距甚远：

The black cat sat on the couch and the brown dog slept on the rug.

单词black在位置 2, pos=2，单词brown在位置 10, pos=10。

我们的问题是找到一种方法来为每个单词的词嵌入添加一个值，以便它具有该信息。但是，我们需要为d模型添加一个值= 512 维！对于每个词嵌入向量，我们需要找到一种方法在和的词嵌入向量i的range(0,512)维度上提供信息。blackbrown

有很多方法可以实现位置编码。本节将重点介绍设计人员使用单位球体表示具有正弦和余弦值的位置编码的巧妙方法，这些值将保持小但有用。

瓦斯瓦尼等人。(2017) 提供正弦和余弦函数，以便我们可以为每个位置和每个维度i的dmodel= 512 的词嵌入向量生成不同的位置编码 ( PE ) 频率：

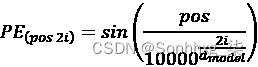
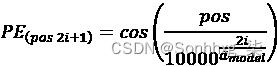
如果我们开始在词嵌入向量的开头，我们将从constant (512)开始，i=0,并以结束i=511。这意味着正弦函数将应用于偶数，余弦函数将应用于奇数。一些实现方式不同。在这种情况下，正弦函数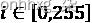的域可以是，余弦函数的域可以是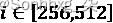。这将产生类似的结果。

在本节中，我们将按照Vaswani等人描述的方式使用这些函数。（2017）。对 Python 伪代码的字面翻译为 position 的位置向量生成以下pe[0][i]代码pos：

def positional_encoding(pos,pe):
for i in range(0, 512,2):
         pe[0][i] = math.sin(pos / (10000 ** ((2 * i)/d_model)))
         pe[0][i+1] = math.cos(pos / (10000 ** ((2 * i)/d_model)))
return pe

Google Brain Trax 和 Hugging Face 等为词嵌入部分和当前位置编码部分提供了现成的库。因此，您无需运行我在本节中分享的代码。但是，如果您想探索代码，可以在 Google Colaboratorypositional_encoding.ipynb笔记本和text.txt本章 GitHub 存储库中的文件中找到它。

在继续之前，您可能希望查看正弦函数的图，例如，对于pos=2.

你可以谷歌以下情节，例如：

plot y=sin(2/10000^(2*x/512))

只是输入情节请求：

图 2.6：使用 Google 绘图

您将获得以下图表：

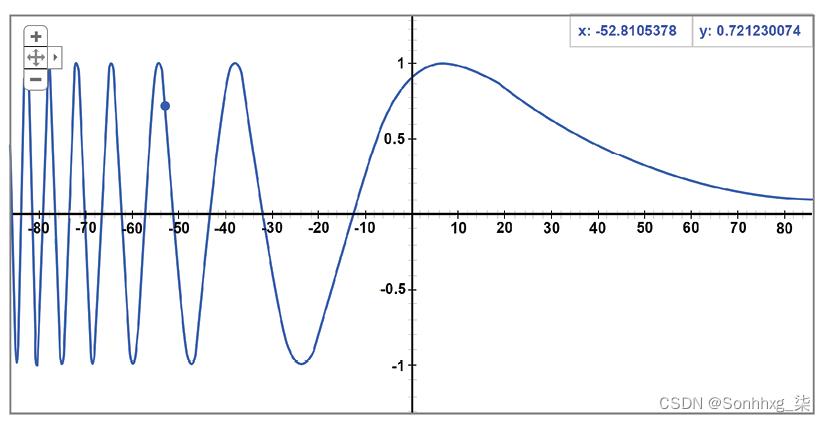图 2.7：图表

如果我们去回到我们在本节中解析的句子，我们可以看到blackis in positionpos=2和brownis in position pos=10：

The black cat sat on the couch and the brown dog slept on the rug.

如果我们申请对于的正弦和余弦函数pos=2，我们得到一个 size=512位置编码向量：

PE(2)= 
[[ 9.09297407e-01 -4.16146845e-01  9.58144367e-01 -2.86285430e-01
   9.87046242e-01 -1.60435960e-01  9.99164224e-01 -4.08766568e-02
   9.97479975e-01  7.09482506e-02  9.84703004e-01  1.74241230e-01
   9.63226616e-01  2.68690288e-01  9.35118318e-01  3.54335666e-01
   9.02130723e-01  4.31462824e-01  8.65725577e-01  5.00518918e-01
   8.27103794e-01  5.62049210e-01  7.87237823e-01  6.16649508e-01
   7.46903539e-01  6.64932430e-01  7.06710517e-01  7.07502782e-01
…
   5.47683925e-08  1.00000000e+00  5.09659337e-08  1.00000000e+00
   4.74274735e-08  1.00000000e+00  4.41346799e-08  1.00000000e+00
   4.10704999e-08  1.00000000e+00  3.82190599e-08  1.00000000e+00
   3.55655878e-08  1.00000000e+00  3.30963417e-08  1.00000000e+00
   3.07985317e-08  1.00000000e+00  2.86602511e-08  1.00000000e+00
   2.66704294e-08  1.00000000e+00  2.48187551e-08  1.00000000e+00
   2.30956392e-08  1.00000000e+00  2.14921574e-08  1.00000000e+00]]

我们也获得一个size=512位置编码向量的位置 10, pos=10：

PE(10)= 
[[-5.44021130e-01 -8.39071512e-01  1.18776485e-01 -9.92920995e-01
   6.92634165e-01 -7.21289039e-01  9.79174793e-01 -2.03019097e-01
   9.37632740e-01  3.47627431e-01  6.40478015e-01  7.67976522e-01
   2.09077001e-01  9.77899194e-01 -2.37917677e-01  9.71285343e-01
  -6.12936735e-01  7.90131986e-01 -8.67519796e-01  4.97402608e-01
  -9.87655997e-01  1.56638563e-01 -9.83699203e-01 -1.79821849e-01
…
  2.73841977e-07  1.00000000e+00  2.54829672e-07  1.00000000e+00
   2.37137371e-07  1.00000000e+00  2.20673414e-07  1.00000000e+00
   2.05352507e-07  1.00000000e+00  1.91095296e-07  1.00000000e+00
   1.77827943e-07  1.00000000e+00  1.65481708e-07  1.00000000e+00
   1.53992659e-07  1.00000000e+00  1.43301250e-07  1.00000000e+00
   1.33352145e-07  1.00000000e+00  1.24093773e-07  1.00000000e+00
   1.15478201e-07  1.00000000e+00  1.07460785e-07  1.00000000e+00]]

什么时候我们查看我们通过Vaswani等人的直观直译获得的结果。(2017) 函数导入 Python，我们想检查结果是否有意义。

用于词嵌入的余弦相似度函数可用于更好地可视化位置的接近度：

cosine_similarity(pos(2), pos(10))= [[0.8600013]]

单词位置的相似性black和brown词汇字段（一起出现的词组）相似性之间的相似性是不同的：

cosine_similarity(black, brown)= [[0.9998901]]

位置的编码显示出比词嵌入相似度更低的相似度值。

位置编码已经把这些词分开了。请记住，词嵌入会因用于训练它们的语料库而异。现在的问题是如何将位置编码添加到词嵌入向量中。

向嵌入向量添加位置编码

作者变压器的通过仅将位置编码向量添加到词嵌入向量中找到了一种简单的方法：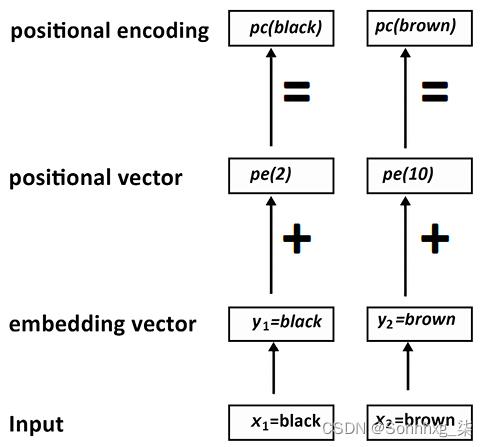

图 2.8：位置编码

如果我们返回并以词嵌入black为例，并将其命名为 y 1 = black，我们就可以将其添加到通过位置编码函数获得的位置向量pe ( 2 )中。我们将获得输入单词black的位置编码 pc(black) ：

pc(black) = y1 + pe(2)

解决方案很简单。但是，如果我们如图所示应用它，我们可能会丢失词嵌入的信息，这将被位置编码向量最小化。

增加 y 1的值有很多可能性，以确保词嵌入层的信息可以在后续层中有效地使用。

许多可能性之一是将任意值添加到 y 1，即的词嵌入black：

y1 * math.sqrt(d_model)

我们可以现在添加位置向量到单词的嵌入向量black，它们的大小相同 ( 512)：

for i in range(0, 512,2):
          pe[0][i] = math.sin(pos / (10000 ** ((2 * i)/d_model)))
          pc[0][i] = (y[0][i]*math.sqrt(d_model))+ pe[0][i]
            
          pe[0][i+1] = math.cos(pos / (10000 ** ((2 * i)/d_model)))
          pc[0][i+1] = (y[0][i+1]*math.sqrt(d_model))+ pe[0][i+1]

得到的结果是最终的维度d model = 512的位置编码向量：

pc(black)=
[[ 9.09297407e-01 -4.16146845e-01  9.58144367e-01 -2.86285430e-01
   9.87046242e-01 -1.60435960e-01  9.99164224e-01 -4.08766568e-02
   …
  4.74274735e-08  1.00000000e+00  4.41346799e-08  1.00000000e+00
   4.10704999e-08  1.00000000e+00  3.82190599e-08  1.00000000e+00
   2.66704294e-08  1.00000000e+00  2.48187551e-08  1.00000000e+00
   2.30956392e-08  1.00000000e+00  2.14921574e-08  1.00000000e+00]]

相同的操作适用于单词brown和序列中的所有其他单词。

我们可以将余弦相似度函数应用于和的位置编码black向量brown：

cosine_similarity(pc(black), pc(brown))= [[0.9627094]]

我们现在通过我们应用于表示单词black和的三个状态的三个余弦相似度函数来清楚地了解位置编码过程brown：

[[0.99987495]] word similarity
[[0.8600013]] positional encoding vector similarity
[[0.9627094]] final positional encoding similarity

我们看到它们嵌入的初始单词相似度很高，值为0.99. 然后我们看到位置 2 和 10 的位置编码向量将这两个词以较低的相似度值拉开0.86。

最后，我们添加了这个词将每个单词的向量嵌入到其各自的位置编码向量中。我们看到这带来了两个词的余弦相似度0.96。

每个词的位置编码现在包含初始词嵌入信息和位置编码值。

位置编码的输出导致多头注意力子层。

子层 1：多头注意力（Sublayer 1: Multi-head attention）

多头注意子层包含八个头，然后是后层归一化，它将向子层的输出添加残差连接并对其进行归一化：

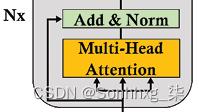
图 2.9：多头注意力子层

本节从注意力层的架构开始。然后，在 Python 中的一个小模块中实现了一个多注意的示例。最后，描述了层后归一化。

让我们从多头注意力的架构开始。

多头注意力的架构

输入编码器堆栈第一层的多注意子层的向量是一个向量，其中包含每个单词的嵌入和位置编码。堆栈的下一层不会重新开始这些操作。

输入序列的每个词x n的向量的维数为d model = 512：

pe(xn)=[d1=9.09297407e-01, d2=-4.16146845e-01, .., d512=1.00000000e+00]

每个词x n的表示都变成了d model = 512 维的向量。

每个单词都映射到所有其他单词以确定它如何适合序列。

在下面的句子中，我们可以看到它可能与cat序列rug相关：

Sequence =The cat sat on the rug and it was dry-cleaned.

该模型将训练找出是否it与cat或相关rug。我们可以像现在一样使用d模型= 512 维来训练模型，从而进行大量计算。

但是，通过使用一个d模型块分析序列，我们一次只能获得一个观点。此外，寻找其他视角需要相当长的计算时间。

一个更好的方法是将d模型= 512维的x（一个序列的所有词）的每个词x n分成8 d k = 64维。

然后，我们可以并行运行 8 个“heads”以加快训练速度，并获得 8 个不同的表示子空间，以了解每个单词与另一个单词的关系：

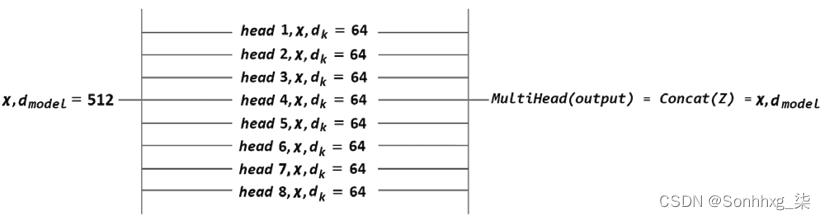图 2.10：多头表示

你可以看到现在有多8个头并行运行。一个人可能会决定it很适合cat，另一个it人很适合rug，另一个人rug很适合dry-cleaned。

每个头的输出是一个形状为x * d k的矩阵Z i。多注意力头的输出是Z定义为：

Z = ( Z 0 , Z 1 , Z 2 , Z 3 , Z 4 , Z 5 , Z 6 , Z 7 )

但是，必须将Z连接起来，以便多头子层的输出不是维度序列，而是xm * d模型矩阵的一行。

在退出多头注意力子层之前，将Z的元素连接起来：

MultiHead(output) = Concat(Z0, Z1, Z2, Z3, Z4, Z5, Z6, Z7) = x, dmodel

请注意，每个头都连接到z中，维度为d model = 512。多头层的输出尊重原始 Transformer 模型的约束。

在注意力机制的每个 head h n中，“单词”矩阵具有三种表示形式：

一个查询矩阵 ( Q )具有d q = 64 的维度，它寻找“单词”矩阵的所有键值对。
一个关键矩阵 ( K )具有d k = 64 的维度，将对其进行训练以提供注意力值。
一个值矩阵 ( V )具有d v = 64 的维度，它将被训练以提供另一个注意力值。

注意力被定义为“Scaled Dot-Product Attention”，用下面的公式表示，我们在其中插入Q、K和V：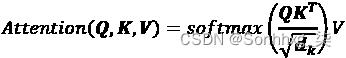

矩阵都具有相同的维度，因此使用缩放点积来获得每个头部的注意力值然后连接 8 个头部的输出Z变得相对简单。

要获得Q、K和V，我们必须使用它们的权重矩阵Q w、K w和V w来训练模型，其中d k =64 列和d model = 512 行。例如，Q是通过x和Q w之间的点积获得的。Q的维度为d k =64。

您可以修改 Transformer 的所有参数，例如层数、heads、d model、d k和其他变量以适合您的模型。本章描述了Vaswani等人的原始 Transformer 参数。（2017）。在修改原始架构或探索其他人设计的原始模型的变体之前，必须了解原始架构。

Google Brain Trax、OpenAI 和 Hugging Face 等提供了现成的库，我们将在本书中使用这些库。

然而，让我们打开 Transformer 模型的引擎盖，用 Python 来说明一下我们刚刚探索的架构，以在代码中可视化模型并用中间图像显示它。

我们将使用基本的 Python 代码numpy和一个softmax函数，分 10 个步骤来运行注意力机制的关键方面。

请记住，工业 4.0 开发人员将面临针对同一算法的多种架构的挑战。

现在让我们开始构建模型的第 1 步来表示输入。

第 1 步：表示输入

保存Multi_Head_Attention_Sub_Layer.ipynb到您的 Google Drive（确保您有 Gmail 帐户），然后在 Google Colaboratory 中打开它。该笔记本位于本章的 GitHub 存储库中。

我们将首先仅使用最少的 Python 函数来了解低级别的 Transformer，以及注意力头的内部工作原理。我们将使用基本代码探索多头注意力子层的内部工作原理：

import numpy as np
from scipy.special import softmax

我们正在构建的注意力机制的输入被缩小到d model ==4 而不是d model = 512。这将输入x的向量的维度缩小到d model =4，这更容易可视化。

x包含每个维度的3输入，4而不是512：

print("Step 1: Input : 3 inputs, d_model=4")
x =np.array([[1.0, 0.0, 1.0, 0.0],   # Input 1
             [0.0, 2.0, 0.0, 2.0],   # Input 2
             [1.0, 1.0, 1.0, 1.0]])  # Input 3
print(x)

输出显示我们有 3 个d model =4 的向量：

Step 1: Input : 3 inputs, d_model=4
[[1. 0. 1. 0.]
 [0. 2. 0. 2.]
 [1. 1. 1. 1.]]

我们模型的第一步已经准备好了：

图 2.11：多头注意力子层的输入

我们将现在将权重矩阵添加到我们的模型中。

第 2 步：初始化权重矩阵

每个输入有 3 个权重矩阵：

Q w训练查询
K w训练密钥
V w训练值

这 3 个权重矩阵将应用于此模型中的所有输入。

Vaswani等人描述的权重矩阵。(2017) 是d K ==64 维。但是，让我们将矩阵缩小到d K ==3。维度被缩小为3*4权重矩阵，以便能够更轻松地可视化中间结果并使用输入x执行点积。

这个教育笔记本中矩阵的大小和形状是任意的。目标是通过注意力机制的整个过程。

三个权重矩阵从查询权重矩阵开始初始化：

print("Step 2: weights 3 dimensions x d_model=4")
print("w_query")
w_query =np.array([[1, 0, 1],
                   [1, 0, 0],
                   [0, 0, 1],
                   [0, 1, 1]])
print(w_query)

输出是w_query权重矩阵：

w_query
[[1 0 1]
 [1 0 0]
 [0 0 1]
 [0 1 1]]

我们现在将初始化关键权重矩阵：

print("w_key")
w_key =np.array([[0, 0, 1],
                 [1, 1, 0],
                 [0, 1, 0],
                 [1, 1, 0]])
print(w_key)

输出是关键权重矩阵：

w_key
[[0 0 1]
 [1 1 0]
 [0 1 0]
 [1 1 0]]

最后，我们初始化值权重矩阵：

print("w_value")
w_value = np.array([[0, 2, 0],
                    [0, 3, 0],
                    [1, 0, 3],
                    [1, 1, 0]])
print(w_value)

输出是值权重矩阵：

w_value
[[0 2 0]
 [0 3 0]
 [1 0 3]
 [1 1 0]]

我们模型的第二步就准备好了：

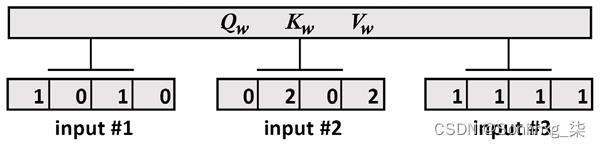
图 2.12：添加到模型中的权重矩阵

我们将现在将权重乘以输入向量以获得Q、K和V。

步骤 3：矩阵乘法以获得 Q、K 和 V

我们将现在将输入向量乘以权重矩阵以获得查询、键和值每个输入的向量。

在在这个模型中，我们将假设所有输入都有一个w_query、w_key和w_value权重矩阵。其他方法是可能的。

让我们首先将输入向量乘以w_query权重矩阵：

print("Step 3: Matrix multiplication to obtain Q,K,V")
print("Query: x * w_query")
Q=np.matmul(x,w_query)
print(Q)

输出是Q 1 ==64= [1, 0, 2]、Q 2 = [2,2, 2] 和Q 3 = [2,1, 3] 的向量：

Step 3: Matrix multiplication to obtain Q,K,V
Query: x * w_query
[[1. 0. 2.]
 [2. 2. 2.]
 [2. 1. 3.]]

我们现在将输入向量乘以w_key权重矩阵：

print("Key: x * w_key")
K=np.matmul(x,w_key)
print(K)

我们得到K 1 = [0, 1, 1]、K 2 = [4, 4, 0] 和K 3 = [2 ,3, 1] 的向量：

Key: x * w_key
[[0. 1. 1.]
 [4. 4. 0.]
 [2. 3. 1.]]

最后，我们将输入向量乘以w_value权重矩阵：

print("Value: x * w_value")
V=np.matmul(x,w_value)
print(V)

我们获得V 1 = [1, 2, 3]、V 2 = [2, 8, 0] 和V 3 = [2 ,6, 3] 的向量：

Value: x * w_value
[[1. 2. 3.]
 [2. 8. 0.]
 [2. 6. 3.]]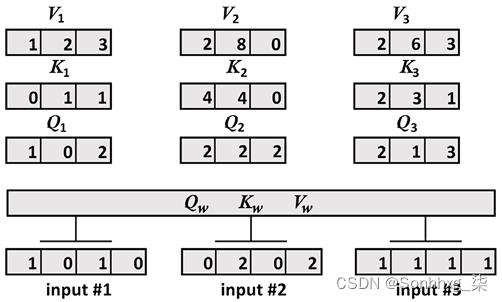

这第三步我们的模型准备好了：

图 2.13：生成 Q、K 和 V

我们有计算注意力分数所需的Q、K和V值。

第 4 步：按比例缩放的注意力分数

这attention head 现在实现了原始的 Transformer 方程：

Transformer模型

1、《Attention Is All You Need》

2、CV中应用Transformer，图像数据转换为序列即可开始使用

新一代backbone，用于分类，分割，检测等任务

对输入序列进行特征提取，下面是transformer的工作流程：

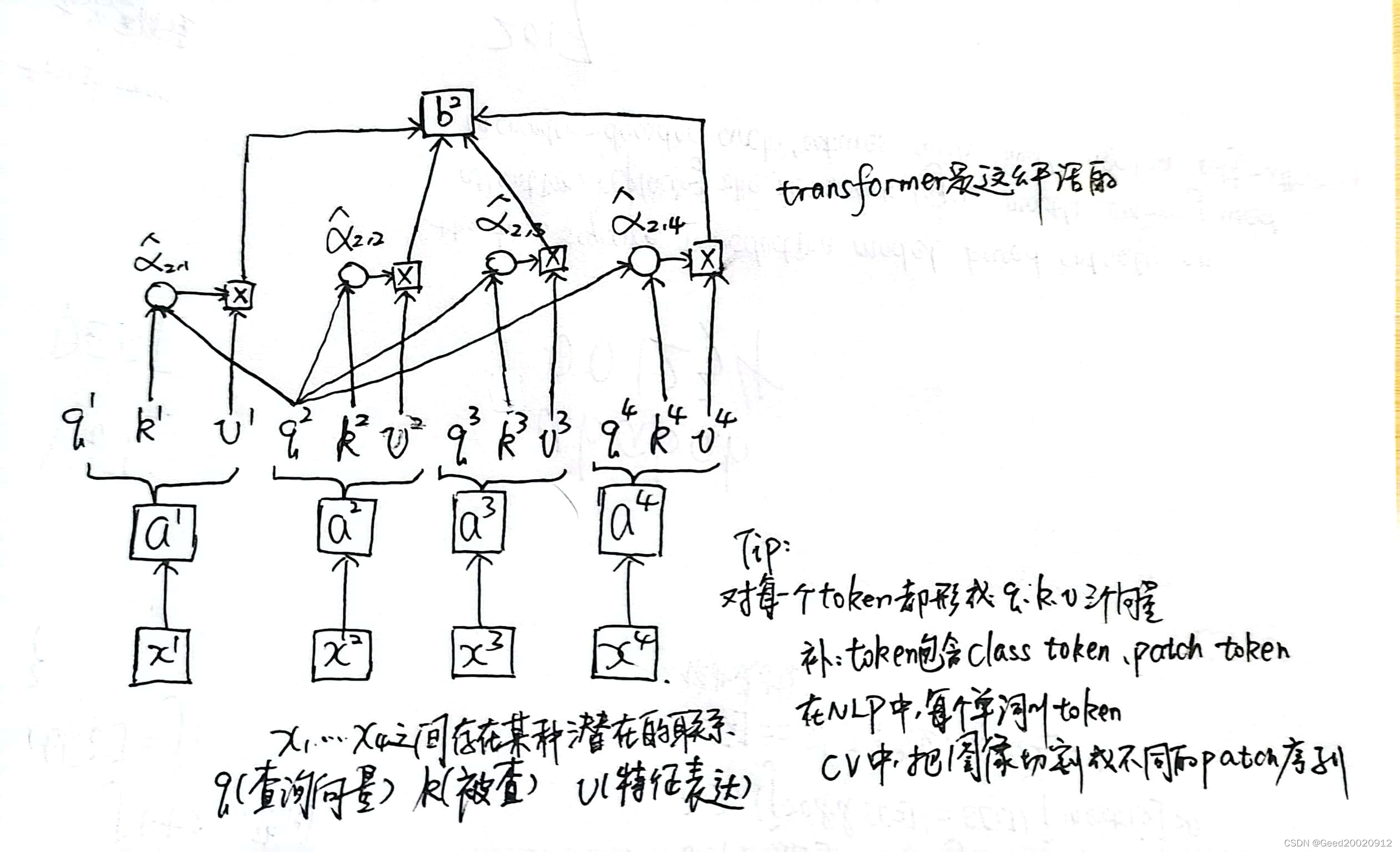
视觉中的Attention：关注需要关注的目标，方便提取特征

ViT整体架构分析

位置编码：1）0-9

2）按照坐标形式编码

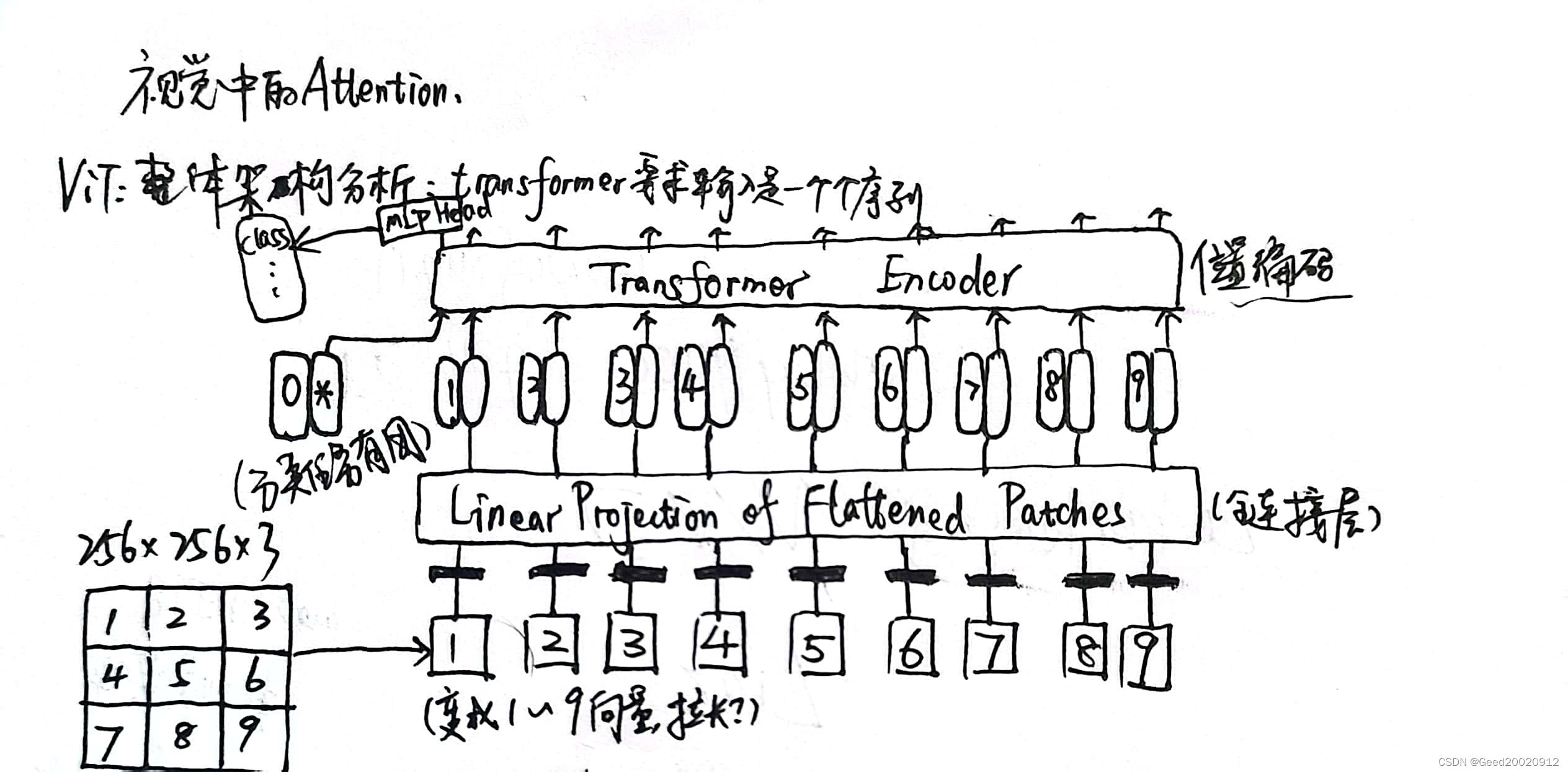
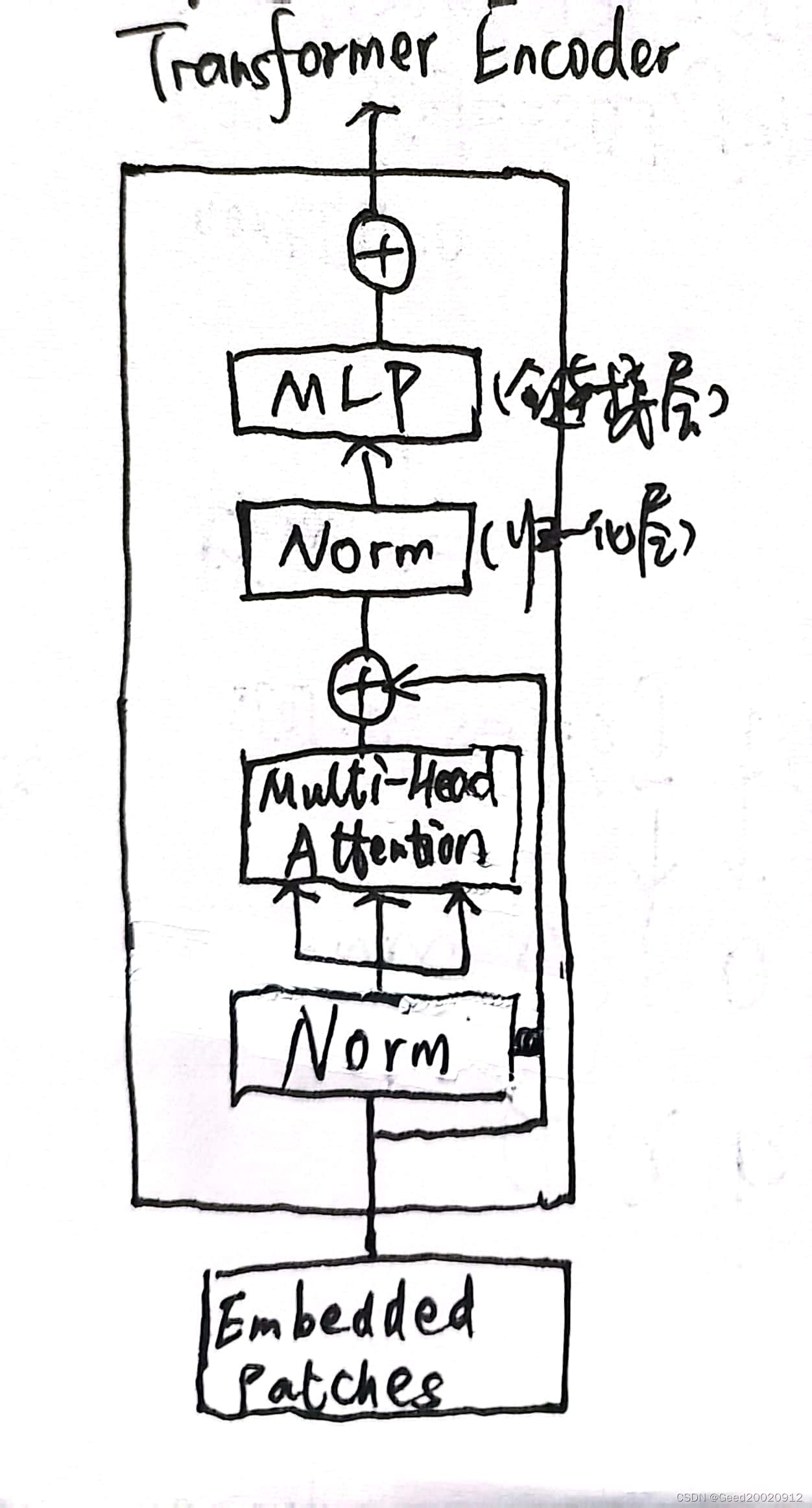
CNN的问题与缺陷

1、想要获得大的感受野就必须堆叠很多层卷积

2、不断卷积＋池化的操作有点麻烦

transformer根本不需要堆叠，直接可以获得全局信息，但是transformer的训练数据必须到位

以上是关于开始使用 Transformer 模型的架构的主要内容，如果未能解决你的问题，请参考以下文章

关于 Transformer 的面试题

开始使用 Transformer 模型的架构

Transformer机器学习模型，不懂就看这里！

深度学习之自然语言处理BERT