斐波那契数列两种算法和青蛙跳台阶的两种实际问题

Posted 2023-04-02 洁洁啊

首先来看一下斐波那契数列的定义

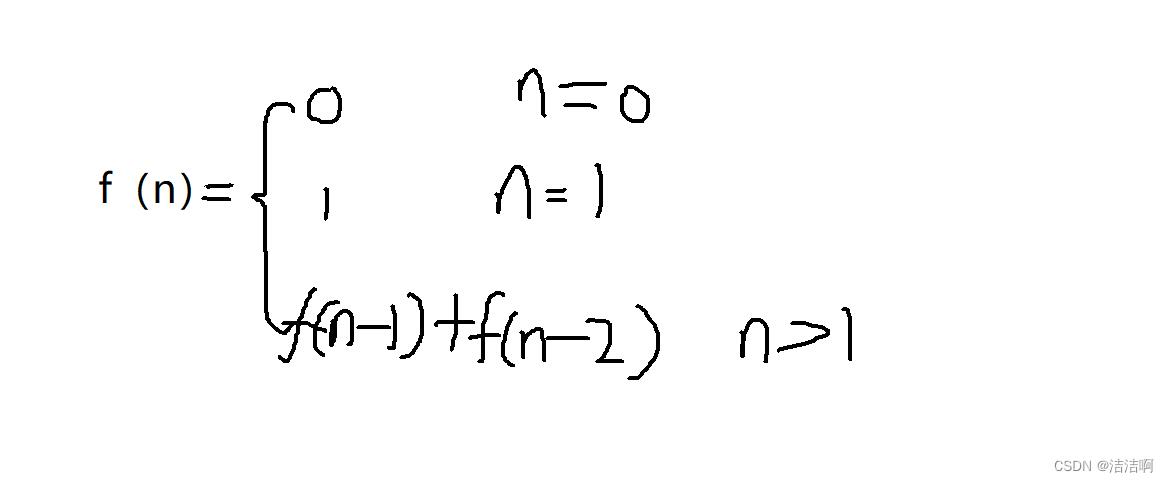
当我们看到这样的题时，心想就是一个简单的递归调用么。
但是，我们要看到这种算法的不足之处——效率低下。
首先简单的介绍一下 ：

递归算法：

long long Fibonacci(unsigned int n)

	if (n <= 0)
		return 0;
	if (n == 1)
		return 1;
	return Fibonacci(n - 1) + Fibonacci(n - 2);

简单分析一下这种递归算法
当n是0时，返回0；
当n是1时，返回1；
当n大于1时 ，返回f（n-1）+f（n-2）；
它是先递归到最后一个数据时，再从后往前算。
假设n为 5 则如下图所示：

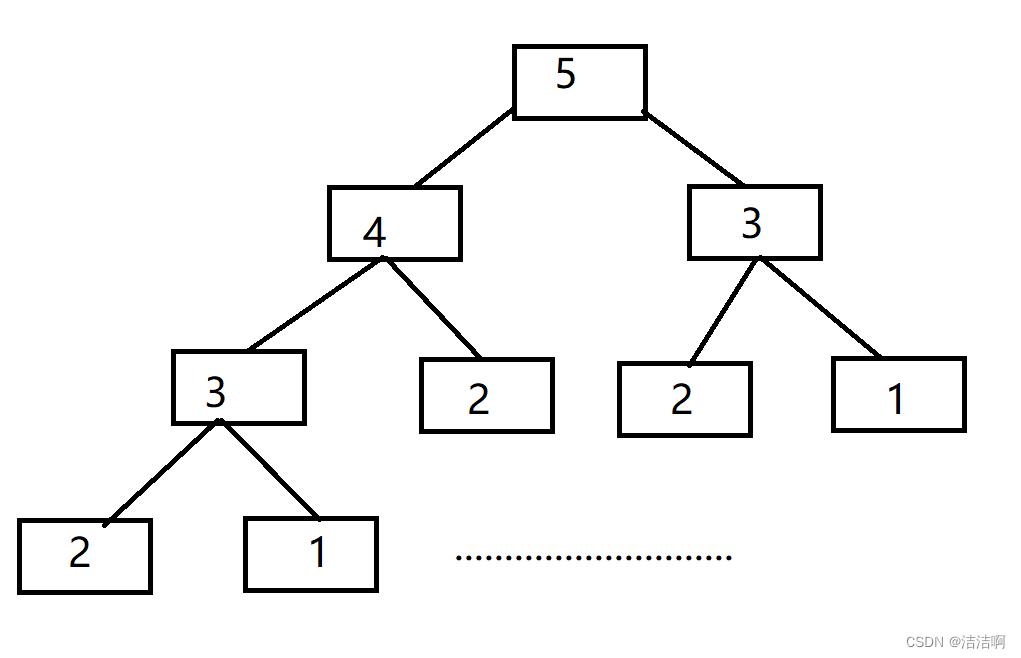
通过此图可以看出。在递归调用时，会有元素被重复调用，当数据n 的数量太大时，效率就会变得非常慢。
所以我们就要来想个办法来解决这个问题。

递归变循环算法：

long long Fibonacci(unsigned int n)

	int result[2] =  0,1 ;
	if (n < 2)
		return result[n];
	long long fibnOne = 0;
	long long fibnTwo = 1;
	long long fibn = 0;
	for (int i = 2; i <= n; i++)
	
		fibn = fibnOne + fibnTwo;
		fibnOne = fibnTwo;
		fibnTwo = fibn;
	
	return fibn;

把递归的算法转化成循坏的算法，该算法时间复杂度是O（n）
效率得到了大大的提升。

青蛙跳台阶问题

第一种：

一只青蛙一次可以跳1级台阶，也可以一次跳2级台阶，求该青蛙·跳上n级台阶总共有几种跳法？
分析：
当我们拿到一个实际问题时，不会的话也不要慌，不管什么题它一定存在内在的逻辑关系。不管题目有多花里胡哨，它的·本质是不会变的，只要结合所学的知识，抓住本质，一步一步来，就能迎刃而解！
首先考虑最简单的·情况：
当n是1时 ，只有一种跳法
当n是2时，可以先跳一步再跳一步 。或者一下跳两步。 所以有两种跳法。
当n 是3时， 可一步一步跳，或者先跳一步再跳两步 或者先跳两步再跳一步。所以一共有3种跳法。
当n 是4时，可一步一步跳，可先跳一步再跳一步再跳两步，可先跳一步再跳两步再跳一步，可先跳两步再跳一步再跳一步，可先跳两步再跳两步。所以一共有5种跳法。

算到这的时候就会有人看出来了，这是一个斐波那契数列。前两项的和等于第三项。
没有看出来的，也不要着急，再算一下n为5时的跳法，会更容易得出结论，或者不确定结论时，算一下来验证一下都可以。

#include <stdio.h>

long long Fibonacci(unsigned int n)

	if (n <=0)
		return 0;
	if (n == 1)
		return 1;
	if (n == 2)
		return 2;
	return Fibonacci(n - 1) + Fibonacci(n - 2);

int main()


	int n = 3;
	printf("%d",Fibonacci(n));
    
	return 0;

第二种

一只青蛙可以一次跳上一级，可以一次跳两级，也可以跳三级…也可以一次跳n级。 求此时青蛙跳上一个n级的台阶一共有几种跳法？

不会做，不要慌。首先来确定这道题本质是什么。即数学思维 ，以小推大，从小来找规律。

当n是1 时，只有一种跳法
当n 是2时，可一次跳两级，可一次跳一级再跳一级。一共有2种跳法。
当n 是3时，可一次跳三级，可一次跳一级再跳两级，可一次跳两级再跳一级，可一次跳一级再跳一级再跳一级。一共有4种跳法。
…
这里·可以用数学归纳法来证明f（n）=2^n-1

其它相关题目

用21的小矩形横着或者竖着去覆盖一个更大的矩形，比如去覆盖一个28的大矩形，总共有多少种方法？
如图所示：

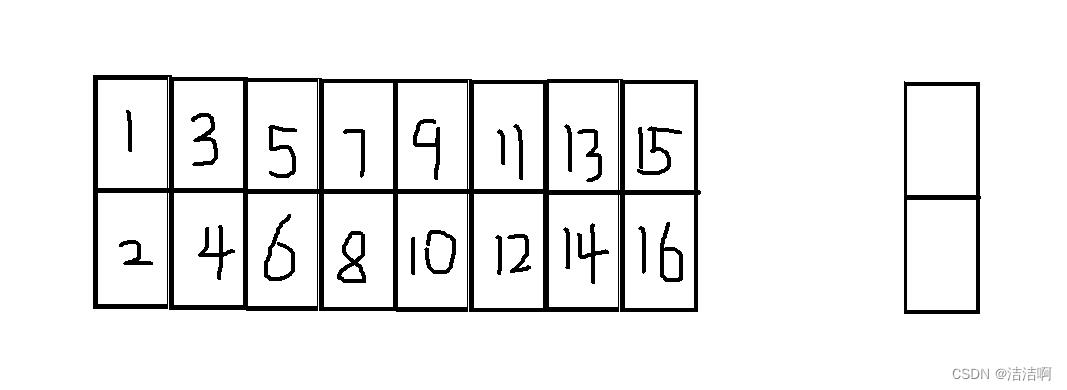
可以把28的覆盖方法记为f（8）
当把21的小矩形去覆盖大矩形的最左边时有两种选择：横着放，竖着放。
当竖着放的时候（1 2位置），后面还有27个矩形，也就是有f（7）种方法。
当横着放的时候（1 3位置），则下面的2 4 也要必须横着放。还剩下26个矩形，也就是f（6）种方法。
所以f（8）=f（7）+f（6）；
所以可以看出又是一个斐波那契数列。
最后可以看出 f（2）是2 ，f（1）是1；

青蛙跳问题为什么是斐波那契数列

• 在面试中我们可能会遇到青蛙跳的问题：一只青蛙一次可以跳上一级台阶，或者跳上二级台阶。那么如果总共有N级台阶，问这只青蛙总共有多少种跳法？
• 首先，我们考虑最简单的情况，如果只有一级台阶，那显然青蛙只有一种跳法。如果只有二级台阶，那么青蛙就有两种跳法，一种是每次跳一级，总共跳二次，另一种就是直接跳二级。
• 接下来，再来看N级的（N大于2）的情况。我们先把N级台阶的跳法看做一个N的函数，记为f(N)。考虑N>2时，第一次跳就有两种跳法，一种是第一次只跳一级，此时跳法数就是后面剩下的N-1级台阶的跳法数，即为f(N-1)；另一种则是第一次跳二级，那么此时的跳法数就是后面剩下的N-2级台阶的跳法数，即为f(N-2)。所以，N级台阶的跳法总数就是f(N)=f(N-1)+f(N-2)。显然这就是一个N>0的斐波那契数列。
• C++实现递归解法

#include<iostream> 
using namespace std; 

long long RecursiveFibonacci(unsigned int n)
{
    if(n == 1 || n == 2)
        return n;

    return RecursiveFibonacci(n-1) + RecursiveFibonacci(n-2);
}

int main() 
{
    cout << "RecursiveFibonacci(1)=" << RecursiveFibonacci(1) << endl;
    cout << "RecursiveFibonacci(2)=" << RecursiveFibonacci(2) << endl;
    cout << "RecursiveFibonacci(3)=" << RecursiveFibonacci(3) << endl;
    cout << "RecursiveFibonacci(5)=" << RecursiveFibonacci(5) << endl;
    cout << "RecursiveFibonacci(10)=" << RecursiveFibonacci(10) << endl;
    cout << "RecursiveFibonacci(50)=" << RecursiveFibonacci(50) << endl;
    cout << "RecursiveFibonacci(100)=" << RecursiveFibonacci(100) << endl;
}

• 很显然，递归实现效率是非常低的，其时间复杂度是n的指数级。因为递归存在着大量的重复计算，大家也可以自己跑代码试试，递归去计算n=50就非常慢了。
• 所以，优化思路就是从前往后计算，先根据f(1)和f(2)算f(3)，在根据f(2)和f(3)算f(4)，以此类推算出f(N)。其时间复杂度是O(n)。
• C++实现非递归解法

#include<iostream> 
using namespace std; 

long long NonRecursiveFibonacci(unsigned int n)
{
    if(n == 1 || n == 2)
        return n;

    long long n1 = 1;
    long long n2 = 2;
    long long result = 0;
    for (unsigned int i = 3; i <= n; i++)
    {   
        result = n1 + n2;
        n1 = n2;
        n2 = result;
    }
    return result;
}

int main() 
{
    cout << "NonRecursiveFibonacci(1)=" << NonRecursiveFibonacci(1) << endl;
    cout << "NonRecursiveFibonacci(2)=" << NonRecursiveFibonacci(2) << endl;
    cout << "NonRecursiveFibonacci(3)=" << NonRecursiveFibonacci(3) << endl;
    cout << "NonRecursiveFibonacci(5)=" << NonRecursiveFibonacci(5) << endl;
    cout << "NonRecursiveFibonacci(10)=" << NonRecursiveFibonacci(10) << endl;
    cout << "NonRecursiveFibonacci(50)=" << NonRecursiveFibonacci(50) << endl;
    cout << "NonRecursiveFibonacci(100)=" << NonRecursiveFibonacci(100) << endl;
}