Unity --- 3维数学 --- vector类 --- 三角函数

Posted 2023-04-01 Metallic Cat

  

 

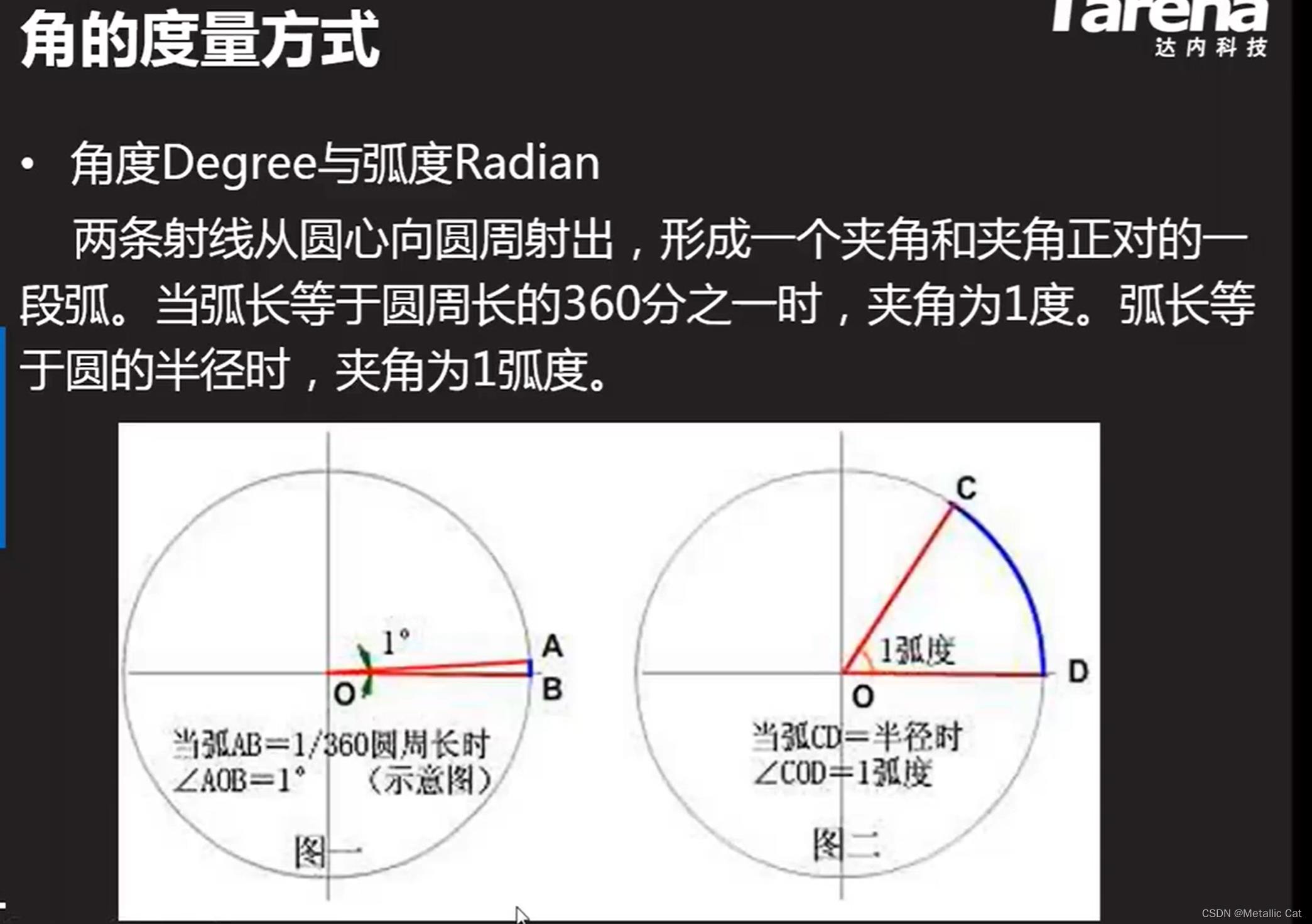
1.Π = 180°，Π是弧度制

 1.利用公式来实现已知角度求弧度

2. 获取Π的方式 --- Mathf类调用静态属 -- PI

3.劳记公式 --- 1Π = 180° --- 也就是说 1° = Π/180 ---》 已知角度的话就能通过直接相乘的方式获得对应的弧度（弧度转角度同理）

4.除了通过调用PI并用公式来计算的方法之外，我们还可以通过调用Mathf类中的静态属性Deg2Rad并与角度相乘来获得对应的弧度 ---- 其实Deg2Rad的全称是 Degree(角度)ToRadian(弧度)，2（two --- 谐音To） --- 即角度转弧度需要乘的数

 

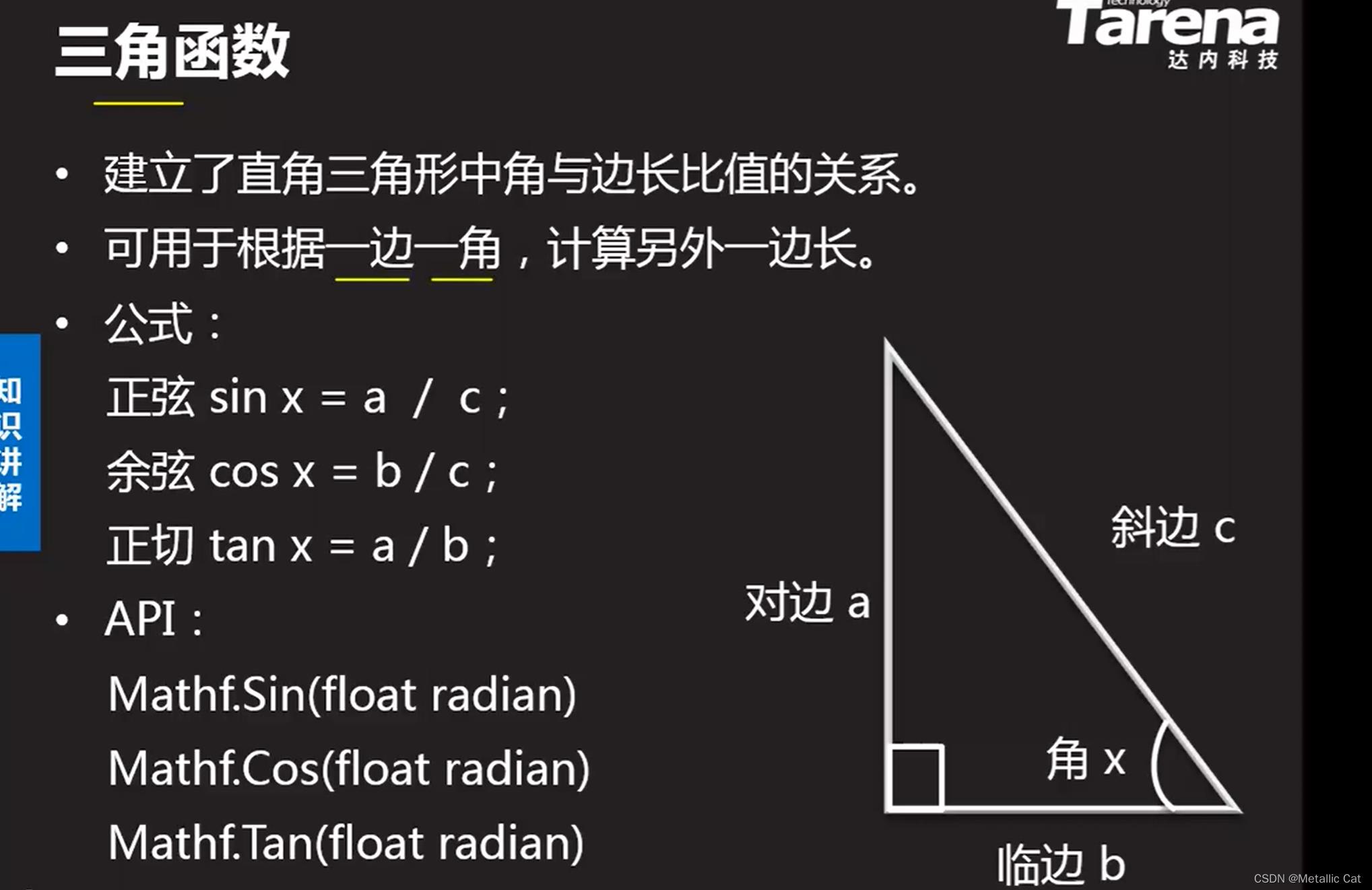
 1.注意！Unity中的三角函数方法需要的参数是弧度，而不是角度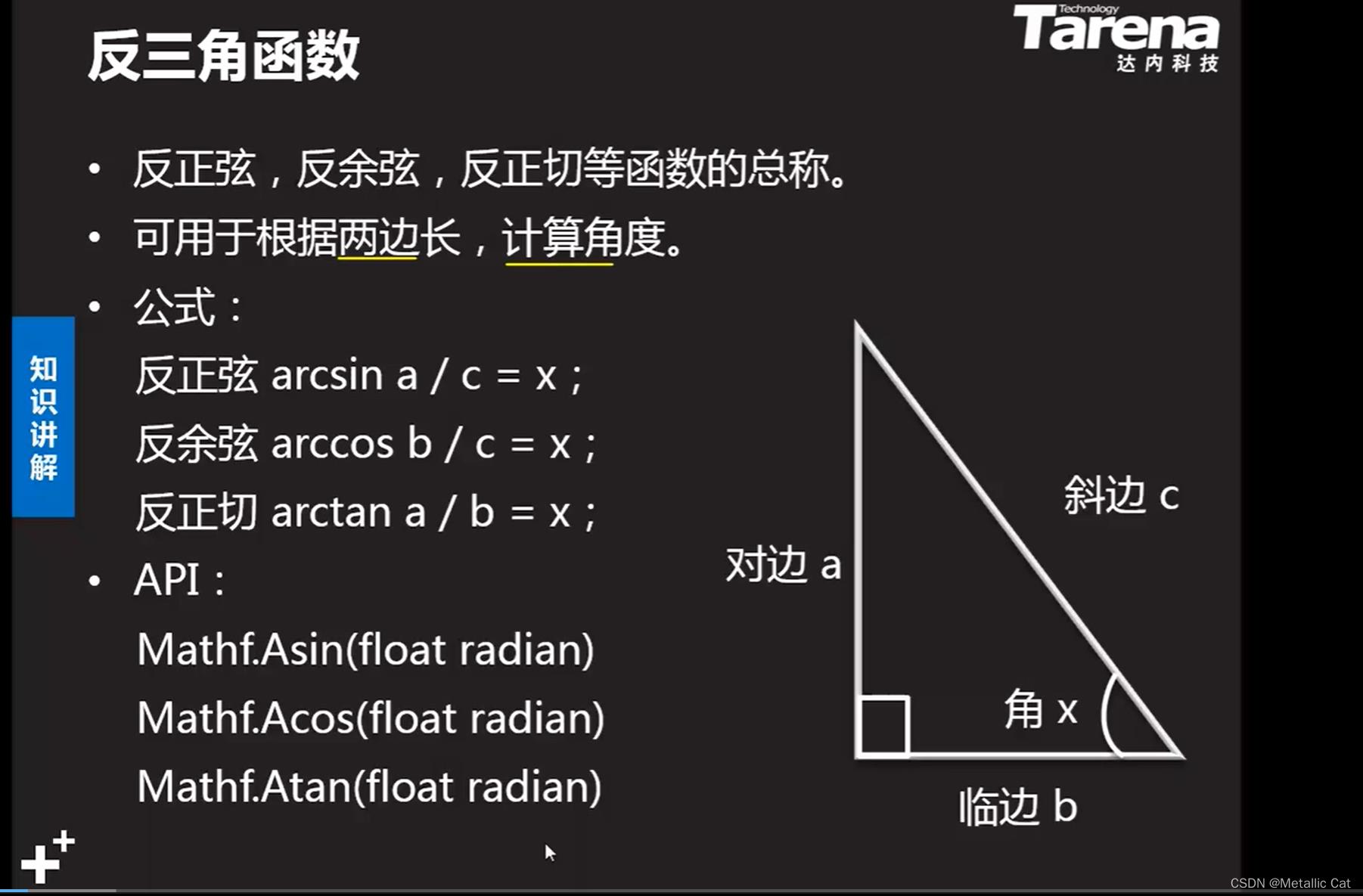

1.反三角函数的作用就是根据两个已知边来求一个未知角

2.注意Unity中的反三角函数方法最后返回的是对应的弧度

1.已知两边求角度的步骤是 --- 获得两边比值，作为参数传给对应的反三角函数方法（Mathf.Atan/Asin/Acos）,将方法的返回值（弧度）转换为角度（乘以Mathf.Rad2Deg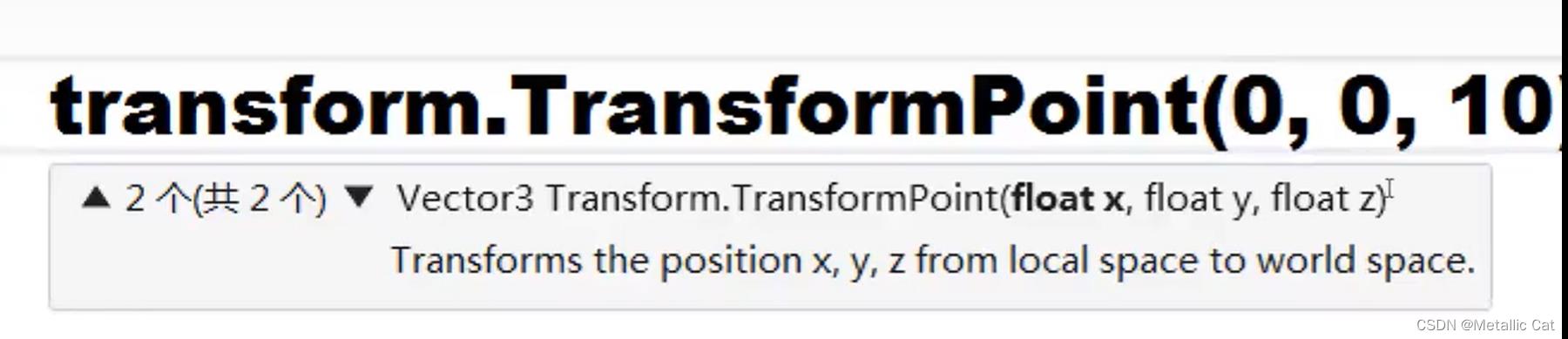）1.TransformPoint方法需要的参数是一个相对于本地坐标系的点的本地坐标系坐标，其作用是将这个点的本地坐标系坐标转换为相对应的世界坐标系中的坐标

（PS：本地坐标系指的就是物体本身的坐标系，上面这样一个方法的调用就是将处于物体本身的坐标系（本地坐标系）中坐标为（0，0，10）的点的坐标转换为其对应的世界坐标系的坐标）

1.物体本地坐标系（自身坐标系）的原点是物体的轴心点

1.调用点乘方法的API是：Vector3.Dot(传要进行点乘的两个向量)

2.向量点乘后得到的结果是一个标量

3.只能够向量除以数字，不能够数字除以向量 

1.Cross --- 是叉乘，Dot是点乘 

2.向量点乘常常用来求两个向量之间的夹角 --- 求取方式：首先两个向量之间的夹角与其模长无关，只与其方向相关，所以我们可以通过单位向量来求 --- 单位向量模长为1

首先获得两个进行点乘的向量的单位向量（nomorlized），然后将这两个单位向量作为参数传给点乘方法Dot，Dot的返回值就等于两个向量之间的夹角的Cos值

（由于单位向量模长为1，再结合公式就能得到上面这个结论）

3.获得两向量之间的夹角的Cos值之后，如果想获得两向量之间的夹角的话，可以使用反三角函数

将我们得到的夹角的Cos值作为参数传给Mathf.Acos()方法，方法会返回夹角对应的弧度值

然后再将弧度值 * Mathf.Rad2Deg转化为角度

 

 1.NaN的意思就是没有数字 --- Null a Number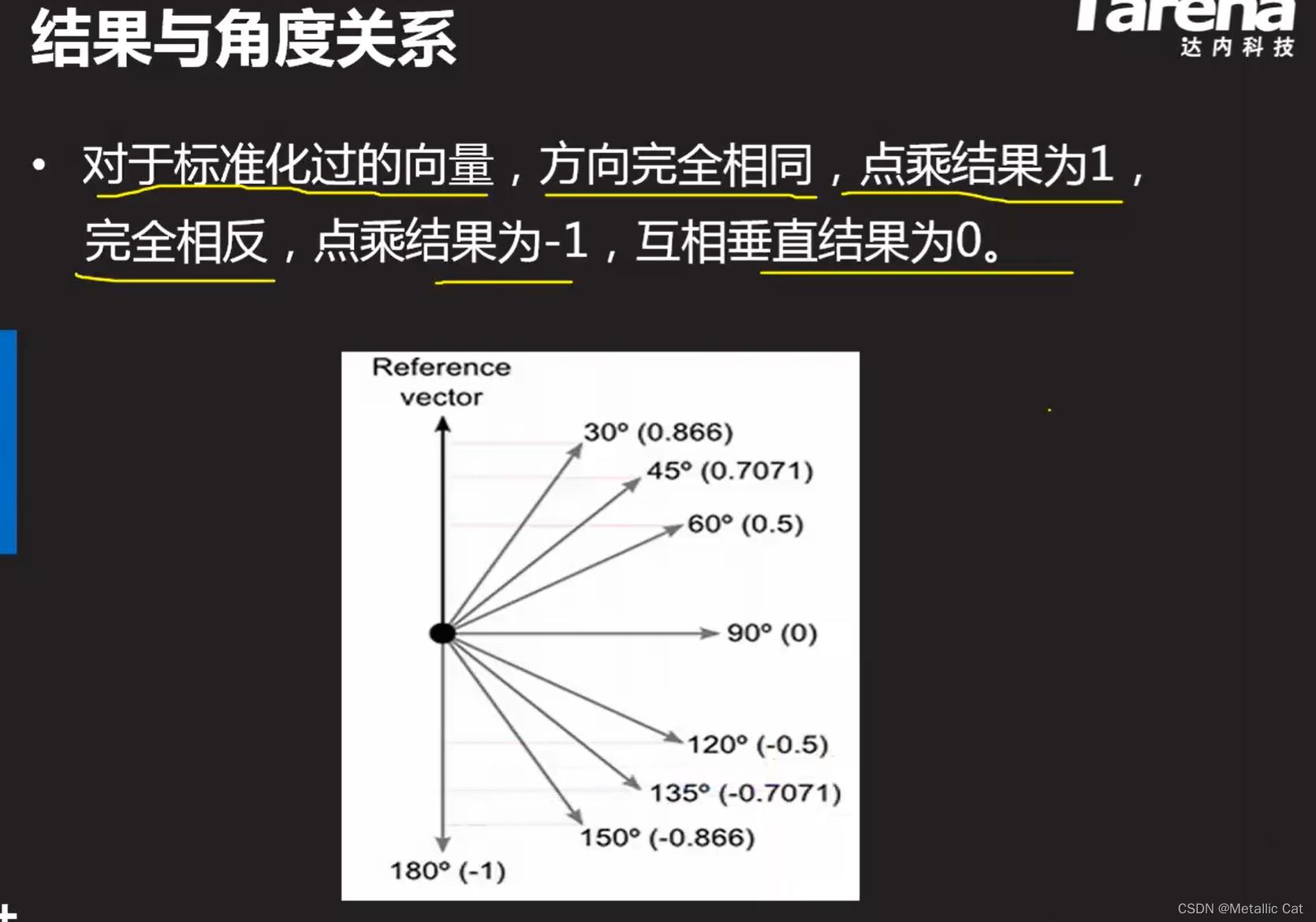

 

 1.两向量叉乘得到的结果是一个新的向量，这个向量的方向与两向量组成的面的法向量一致

其模长是两向量的模长的乘积*两向量的夹角的正弦值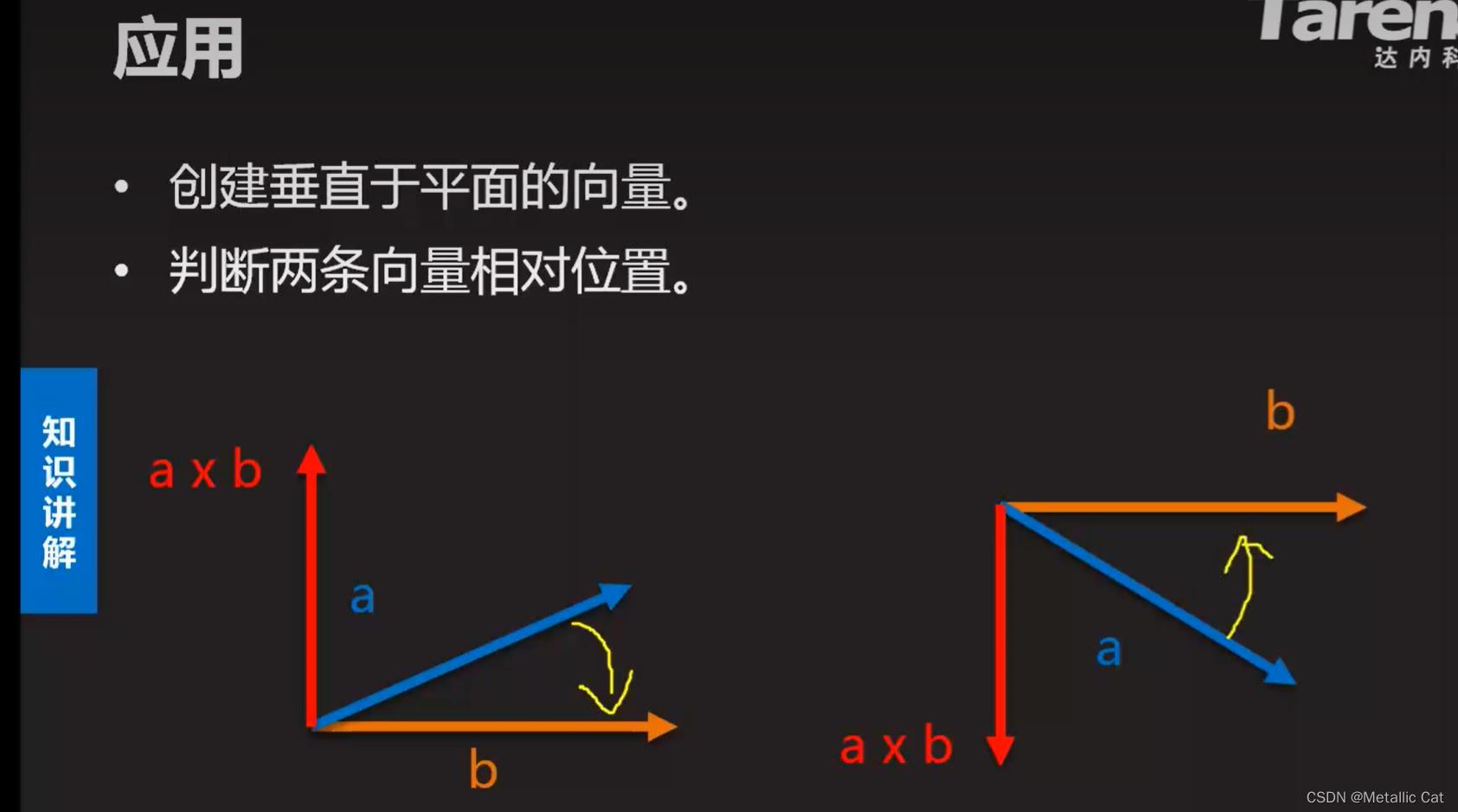

1.如何判断叉乘后得到的向量的方向是垂直向上还是垂直向下？

以向量a叉乘向量b为例：

如果向量a移到向量b处是顺时针关系的话，则方向是垂直向上，反之就是垂直向下（建立在移动最小角度的前提下）

2.通过点乘求得的向量夹角我们是不知道它的正负情况的，但是再结合叉乘就能够判断了

首先通过叉乘求得夹角大小，然后再根据叉乘后得到的向量是垂直向上还是垂直向下来判断角度的正负（向上为正，向下为负）

1.通过叉乘得到的向量是一个Vector3类对象，其本质依然是一个点，当这个点的y轴对应值为负的时候，则表示对应向量的方向是垂直向下的，反之就是垂直向上的。

 1.叉乘通过反正弦能够得到的夹角范围是0 - 90°，而点乘通过反余弦能够得到的夹角范围是0 - 180°，所以我们一般使用点乘来求夹角

1.如何获得物体本地（自身）坐标系的x,y,z轴对应的单位向量在世界坐标系中的向量表示 ?

总共有两种方法：

第一种 --- 利用向量减法与TransformPoint方法来实现 --- 此处以本地坐标系z轴单位向量为例，其它同理：

首先取本地坐标系z轴单位向量（点）（0，0，1），然后将其作为参数传给 TransformPoint 方法获得该点在世界坐标系中对应坐标

然后将本地坐标系原点的坐标（0，0，0）也作为参数传给TransformPoint方法，获得其在世界坐标系中的坐标

规定向量是原点指向z轴单位向量点，则有本地坐标系z轴单位向量在世界坐标系中的向量表示 ---

本地坐标系z轴单位向量在世界坐标系中的坐标 减去 本地坐标系原点在世界坐标系中的坐标

第二种 --- 直接使用Unity已经准备好的静态属性

调用物体的Transfrom类中的静态属性 foward , right , up即可直接获取物体本地坐标系z轴正方向，x轴正方向以及y轴正方向上的单位向量在世界坐标系中的向量表示

（如果想获得反方向的话，加个负号就可以了）

蓝鸥Unity开发基础三课时9 Vector3

【蓝鸥Unity开发基础三】课时9 Vector3

一、Vector3

 

 

 

using UnityEngine;
using System.Collections;

public class Test : MonoBehaviour {

    //Vector3就是一个类，表示向量，向量即有大小又有方向的量
    void Start () {
        Vector3 v = new Vector3 ();
        //x，y，z分别是三个方向上的分量
        float x = v.x;
        float y = v.y;
        float z = v.z;


        //成员方法
        //获取V的单位向量
        //V的长度会变为1,但方向不变
        v.Normalize();

        //返回V方向的单位向量，但是V本身不会发生变化
        Vector3 vn= v.normalized;

        //获取V的长度
        float L=v.magnitude;

        //类方法

        //x=0，y=1，z=0
        Vector3 u=Vector3.up;    //表示世界坐标系中Y轴正方向上的单位向量
        //x=0，y=-1，z=0
        Vector3.down;               //表示世界坐标系中Y轴负方向上的单位向量
        //x=1，y=0，z=0
        Vector3.right;                   //表示世界坐标系中X轴正方向上的单位向量
        //x=-1，y=0，z=0
        Vector3.left;                   //表示世界坐标系中X轴负方向上的单位向量
        //x=0，y=0，z=1
        Vector3.forward;           //表示世界坐标系中Z轴正方向上的单位向量
        //x=0，y=0，z=-1
        Vector3.back;              //表示世界坐标系中Z轴负方向上的单位向量    
        //x=0，y=0，z=0
        Vector3.zero;            //表示原点


        Vector3 v1=new Vector3(1.4f,6f,7.2f);
        Vector3 v2=new Vector3(2f,6.5f,12.3f);
        //求两个向量的夹角
        float angle=Vector3.Angle(v1,v2);


        Vector3 pos1=new Vector3(4f,2f,11f);
        Vector3 pos2=new Vector3(2f,13.6f,8f);
        //求两个点的距离
        float d = Vector3.Distance (pos1,pos2);

        //向量点乘
        float dd= Vector3.Dot(v1,v2);

        //向量差乘
        Vector3 vc=Vector3.Cross(v1,v2);


    }

    void Update () {
    
    }
}

 

推荐视频讲师博客：http://11165165.blog.51cto.com/