Lesson 17.7&17.8&17.9&17.10 调用经典框架&基于resnet与vgg的自建架构&基于普通卷积层和池化层的自建架构&有监督的预训

Posted 2023-03-31 Grateful_Dead424

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Lesson 17.7&17.8&17.9&17.10 调用经典框架&基于resnet与vgg的自建架构&基于普通卷积层和池化层的自建架构&有监督的预训相关的知识，希望对你有一定的参考价值。

2 从经典架构出发

2.1 调用经典架构

我们已经学习了大量经典架构以及他们的经典思想，可以开始考虑自己的架构了。大多数时候，我们不会从0去创造我们的自己的架构，而是在经典架构中挑选一个适合的架构或适合的思路，并在经典架构上依据数据的需要对架构进行自定义和修改（当然了，我们只能够调用我们已经学过、并且掌握原理的架构，否则我们在修改的时候将无从下手）。在PyTorch中，基本所有经典架构都已经被实现了，所以我们可以直接从PyTorch中“调库”来进行使用。遗憾的是，直接调出来的大部分库是无法满足我们自己需求的，但我们还是可以调用PyTorch中的架构类来作为我们自己架构的基础。
在torchvision下，我们已经很熟悉datasets和transforms这两个模块，现在我们需要从torchvision中调用完整的模型架构，这些架构都位于“CV常用模型”模块torchvision.models里。在torchvision.models中，架构/模型被分为4大类型：分类、语义分割、目标检测/实例分割以及关键点检测、视频分类。我们之前学习的经典架构都是最基础的分类架构。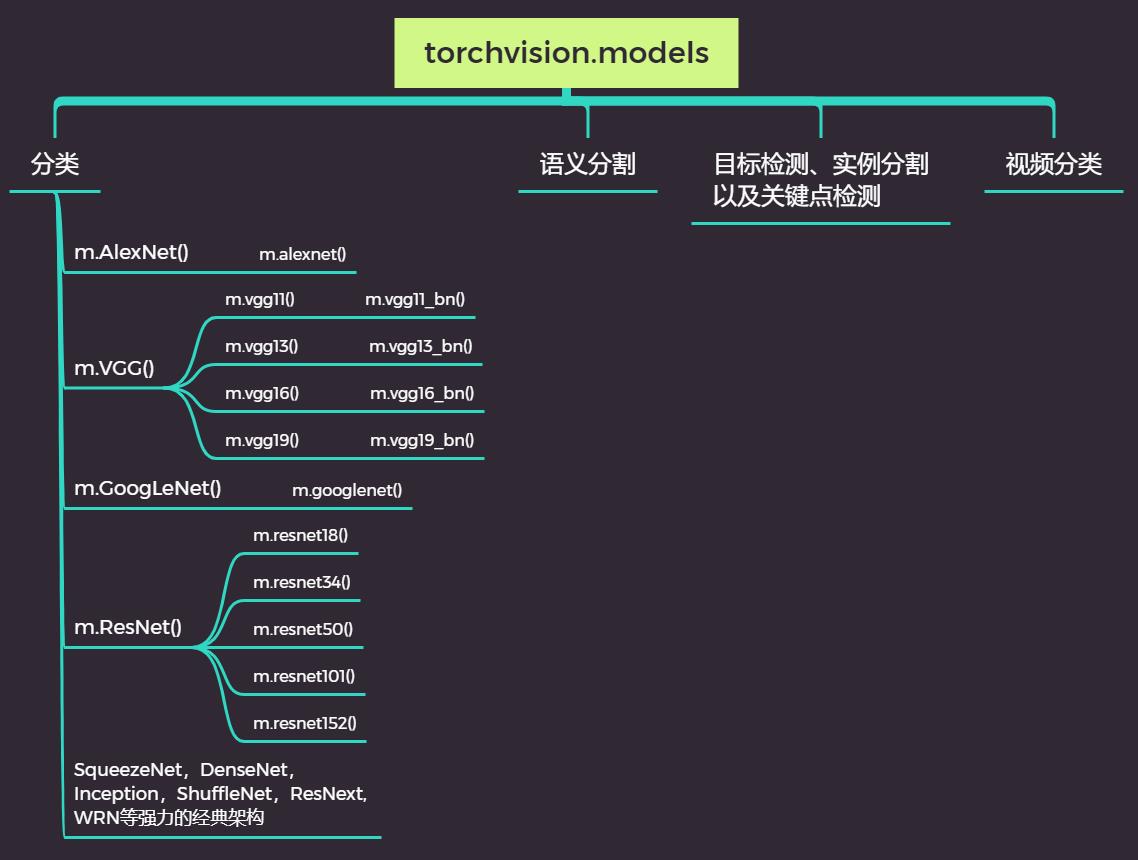
分类架构中包含以AlexNet为代表的、诞生于ILSVRC的各大架构极其变体，也包含了现在被广泛使用的众多融合多种思想的强力架构。对每种类型的架构，models中都包含了至少一个实现架构本身的父类（呈现为“驼峰式”命名）以及一个包含预训练功能的子类（全部小写）。对于拥有不同深度、不同结构的架构而言，可能还包含多个子类。以AlexNet和ResNet为例子：

import torch
import torch.nn as nn
from torchvision import models as m
dir(m)       #查看models里全部的类
#['AlexNet',
# 'DenseNet',
# 'EfficientNet',
# 'GoogLeNet',
# 'GoogLeNetOutputs',
# 'Inception3',
# 'InceptionOutputs',
#
# 'vgg16_bn',
# 'vgg19',
# 'vgg19_bn',
# 'video',
# 'wide_resnet101_2',
# 'wide_resnet50_2']

#对于只有一个架构、不存在不同深度的AlexNet来说，两个类调出的结构是一模一样的
m.AlexNet() #查看需要填写的参数是什么？
m.alexnet() #将AlexNet父类的功能包含在里面，不允许对原始架构进行参数输入，但是可以进行预训练
#对残差网络来说，父类是实现具体架构的类，子类是已经填写好必填参数的类
m.ResNet() #可以从这个类中实现各种不同深度的结构
m.resnet152() #具体的深度和参数都已锁定，可以在这个类上执行预训练

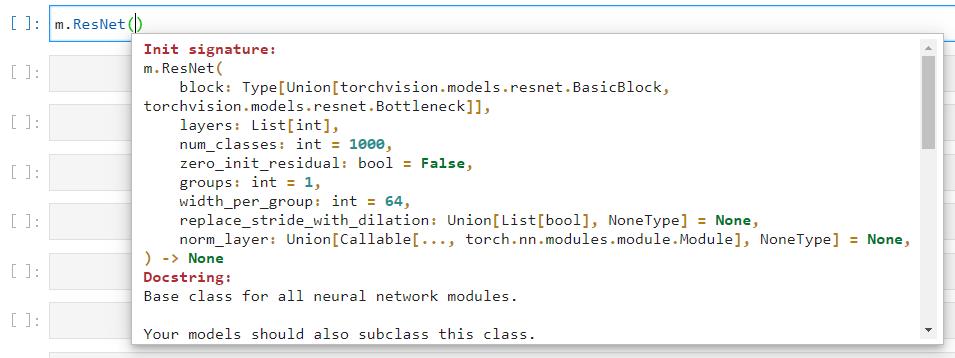
在实际使用模型时，我们几乎总是直接调用小写的类来进行使用，除非我们想大规模修改内部架构。如下所示，调用类的方式非常简单：

import torchvision.models as m #查看每个类中的结构
resnet18_ = m.resnet18()
vgg16_ = m.vgg16()
resnet18_
# ResNet(
#   (conv1): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
#   (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#   (relu): ReLU(inplace=True)
#   (maxpool): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
#   (layer1): Sequential(
#     (0): BasicBlock(
#       (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#       (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       (relu): ReLU(inplace=True)
#       (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#       (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#     )
#     (1): BasicBlock(
#       (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#       (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       (relu): ReLU(inplace=True)
#       (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#       (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#     )
#   )
#   (layer2): Sequential(
#     (0): BasicBlock(
#       (conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
#       (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       (relu): ReLU(inplace=True)
#       (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#       (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       (downsample): Sequential(
#         (0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
#         (1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       )
#     )
#     (1): BasicBlock(
#       (conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#       (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       (relu): ReLU(inplace=True)
#       (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#       (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#     )
#   )
#   (layer3): Sequential(
#     (0): BasicBlock(
#       (conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
#       (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       (relu): ReLU(inplace=True)
#       (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#       (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       (downsample): Sequential(
#         (0): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)
#         (1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       )
#     )
#     (1): BasicBlock(
#       (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#       (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       (relu): ReLU(inplace=True)
#       (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#       (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#     )
#   )
#   (layer4): Sequential(
#     (0): BasicBlock(
#       (conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
#       (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       (relu): ReLU(inplace=True)
#       (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#       (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       (downsample): Sequential(
#         (0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
#         (1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       )
#     )
#     (1): BasicBlock(
#       (conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#       (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#       (relu): ReLU(inplace=True)
#       (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#       (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#     )
#   )
#   (avgpool): AdaptiveAvgPool2d(output_size=(1, 1))
#   (fc): Linear(in_features=512, out_features=1000, bias=True)
# )
resnet18_.conv1
#Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
resnet18_.layer1
# Sequential(
#   (0): BasicBlock(
#     (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#     (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#     (relu): ReLU(inplace=True)
#     (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#     (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#   )
#   (1): BasicBlock(
#     (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#     (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#     (relu): ReLU(inplace=True)
#     (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#     (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#   )
# )
resnet18_.layer1[0]
#BasicBlock(
#  (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#  (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#  (relu): ReLU(inplace=True)
#  (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#  (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#)
resnet18_.layer1[0].conv1
#Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
vgg16_ = m.vgg16()
vgg16_
vgg16_.features[0] 
#需要替换掉整个层
resnet18_
resnet18_.conv1 = nn.Conv2d(1, 64, kernel_size=(7, 7), stride=(2, 2), 
padding=(3, 3), bias=False)
resnet18_.fc = nn.Linear(in_features=512, out_features=10, bias=True)
resnet18_ 
#重新实例化
resnet18_ = m.resnet18()
#另一种方式也可以成功修改resnet18_中显示的内容，但是实际输入数据的时候还是会报错
resnet18_.conv1.in_channels = 1
resnet18_ 
data = torch.ones(10,1,224,224)
resnet18_(data)

不难发现，如果我们想要修改经典架构，我们必须逐层修改。而卷积网路的一层可能对后续的所有层都产生影响，因此我们常常只会对网络的输入、输出层进行微调，并不会修改架构的中间层。然而，大部分时候完全套用经典架构都不能满足我们建模的需求，因此我们需要基于经典架构构建我们自己的架构。

2.2 基于经典架构自建架构

尽管修改经典架构是一件冒险的事儿，我们确实有可能存在大规模修改架构的需求：比如说，几乎所有现代经典架构都是基于ImageNet数据集224x224的尺寸、1000分类构建起来的，因此几乎所有的经典架构都会有5次下采样（池化层或步长为2的卷积层）。当我们的数据集足够大时，我们会优先考虑使用经典架构在数据集上跑一跑，但当我们的图像尺寸较小时，我们不一定需要将图像拓展到224x224的尺寸以适应经典架构（我们的确可以使用transform.Resize这么做，但是放大转换后预测效果不一定会很好）。这样不仅会让算力要求提升、计算时间变长，还不一定能够获得很好的效果。如果可能的话，在较小的图片上，我们希望能够尽量保持原状以控制整体计算量。

对卷积架构来说，改变特征图的输入输出数量的行为只与一两个层有关，要改变特征图尺寸的行为则会影响整个架构。因此，我们一般会从经典架构中“抽取”一部分来进行使用，也有很小的可能会从0建立起自己的新架构。假设我们现在使用的是类似于Fashion-MNIST尺寸的，28x28的数据集，在这样的数据集上，我们可能执行下采样的机会只有2次，一次是从28x28降维到14x14，另一次是从14x14降维到7x7。这样的数据集并不是非常适合几千万、上亿参数的经典架构们。在这种情况下，torchvision.models下自带的架构就不能灵活满足需求，因此我们往往不会直接使用自带架构，而是在自带架构的基础上进行架构重构。接下来我们来学习如何基于经典架构来构筑自己的架构。

#灰度的小数据集（32x32） 
import torch
from torch import nn
from torchvision import models as m
from torchinfo import summary
#ResNet
#卷积层（k=3,p=1） + 残差块 + GLOBALAVG + FC
vgg16_bn_ = m.vgg16_bn()     #带bn层的vgg
resnet18_ = m.resnet18()
vgg16_bn_.features[7:14]
#Sequential(
#  (7): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
#  (8): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#  (9): ReLU(inplace=True)
#  (10): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
#  (11): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#  (12): ReLU(inplace=True)
#  (13): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
#)
resnet18_.layer3
# Sequential(
#   (0): BasicBlock(
#     (conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
#     (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#     (relu): ReLU(inplace=True)
#     (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#     (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#     (downsample): Sequential(
#       (0): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)
#       (1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#     )
#   )
#   (1): BasicBlock(
#     (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#     (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#     (relu): ReLU(inplace=True)
#     (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
#     (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#   )
# )

class MyNet1(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Sequential(nn.Conv2d(1,64,kernel_size=3,stride=1,padding=1)
                                   ,nn.BatchNorm2d(64)
                                   ,nn.ReLU(inplace=True)
                                  )
        self.block2 = vgg16_bn_.features[7:14]
        self.block3 = resnet18_.layer3    #此时特征图的尺寸8*8，特征图的数量为256
        self.avgpool = resnet18_.avgpool #-> 1x1
        self.fc = nn.Linear(in_features=256, out_features=10, bias=True)
        
    def forward(self,x):
        x = self.conv1(x)
        x = self.block3(self.block2(x))
        x = self.avgpool(x)
        x = x.view(x.shape[0],256)
        x = self.fc(x)
        return x
data = torch.ones(10,1,32,32)
net = MyNet1()
net(data).shape
#torch.Size([10, 10])
summary(net,input_size=(10,1,32,32),depth=3,device="cpu")
# ==========================================================================================
# Layer (type:depth-idx)                   Output Shape              Param #
# ==========================================================================================
# ├─Sequential: 1-1                        [10, 64, 32, 32]          --
# |    └─Conv2d: 2-1                       [10, 64, 32, 32]          640
# |    └─BatchNorm2d: 2-2                  [10, 64, 32, 32]          128
# |    └─ReLU: 2-3                         [10, 64, 32, 32]          --
# ├─Sequential: 1-2                        [10, 128, 16, 16]         --
# |    └─Conv2d: 2-4                       [10, 128, 32, 32]         73,856
# |    └─BatchNorm2d: 2-5                  [10, 128, 32, 32]         256
# |    └─ReLU: 2-6                         [10, 128, 32, 32]         --
# |    └─Conv2d: 2-7                       [10, 128, 32, 32]         147,584
# |    └─BatchNorm2d: 2-8                  [10, 128, 32, 32]         256
# |    └─ReLU: 2-9                         [10, 128, 32, 32]         --
# |    └─MaxPool2d: 2-10                   [10, 128, 16, 16]         --
# ├─Sequential: 1-3                        [10, 256, 8, 8]           --
# |    └─BasicBlock: 2-11                  [10, 256, 8, 8]           --
# |    |    └─Conv2d: 3-1                  [10, 256, 8, 8]           294,912
# |    |    └─BatchNorm2d: 3-2             [10, 256, 8, 8]           512
# |    |    └─ReLU: 3-3                    [10, 256, 8, 8]           --
# |    |    └─Conv2d: 3-4                  [10, 256, 8, 8]           589,824
# |    |    └─BatchNorm2d: 3-5             [10, 256, 8, 8]           512
# |    |    └─Sequential: 3-6              [10, 256, 8, 8]           33,280
# |    |    └─ReLU: 3-7                    [10, 256, 8, 8]           --
# |    └─BasicBlock: 2-12                  [10, 256, 8, 8]           --
# |    |    └─Conv2d: 3-8                  [10, 256, 8, 8]           589,824
# |    |    └─BatchNorm2d: 3-9             [10, 256, 8, 8]           512
# |    |    └─ReLU: 3-10                   [10, 256, 8, 8]           --
# |    |    └─Conv2d: 3-11                 [10, 256, 8, 8]           589,824
# |    |    └─BatchNorm2d: 3-12            [10, 256, 8, 8]           512
# |    |    └─ReLU: 3-13                   [10, 256, 8, 8]           --
# ├─AdaptiveAvgPool2d: 1-4                 [10, 256, 1, 1]           --
# ├─Linear: 1-5                            [10, 10]                  2,570
# ==========================================================================================
# Total params: 2,325,002
# Trainable params: 2,325,002
# Non-trainable params: 0
# Total mult-adds (M): 365.76
# ==========================================================================================
# Input size (MB): 0.04
# Forward/backward pass size (MB): 65.54
# Params size (MB): 9.30
# Estimated Total Size (MB): 74.88
# ==========================================================================================

借用经典架构，我们就不必再重新打造整个网络，但缺点是网络的架构和具体的层无法在代码中清晰地显示出来，同时层与层内部的层次结构也不一致，如果我们需要将代码提供给同事或他人进行使用，最好将代码重写为基本层构成的网络，或者准备好完整的批注。

除了在残差网络上进行修改，我们也可以基于VGG的基本思路，打造“又浅又窄”的架构。这种架构虽然在大型数据集上基本无效，但对于Fashion-MNIST来说却可以有很好的结果，并且计算量很小：

class BasicConv2d(nn.Module):
    def __init__(self,in_,out_=10,**kwargs):
        super().__init__()
        self.conv = nn.Sequential(nn.Conv2d(in_,out_,**kwargs)
                                  ,nn.BatchNorm2d(out_)
                                  ,nn.ReLU(inplace=True)
                                 )
    def forward(self,x):
        x = self.conv(x)
        return x
#灰度的小数据集（32x32）
#2卷积+池化 + 3卷积+池化 + 2个线性层 - AlexNet

#找到泛化能力最强的模型/架构
#1、先建立一个欠拟合的模型，加深层、加特征图数量、加参数 - 能够拟合的程度
#2、先建立一个过拟合的模型，减去层、减去特征图数量、加上抗过拟合的参数 - 正常的程度
class MyNet2(nn.Module):
    def __init__(self,in_channels=1,out_features=10):
        super().__init__()
        self.block1 = nn.Sequential(BasicConv2d(in_ = in_channels,out_=32,kernel_size=5,padding=2)
                                    ,BasicConv2d(32,32,kernel_size=5,padding=2)
                                    ,nn.MaxPool2d(2)
                                    ,nn.Dropout2d(0.25))
        self.block2 = nn.Sequential(BasicConv2d(32,64,kernel_size=3,padding=1)
                                   ,BasicConv2d(64,64,kernel_size=3,padding=1)
                                   ,BasicConv2d(64,64,kernel_size=3,padding=1)
                                   ,nn.MaxPool2d(2)
                                   ,nn.Dropout2d(0.25))
        
        self.classifier_ = nn.Sequential(
            nn.Linear(64*7*7,256)
            ,nn.BatchNorm1d(256) #此时数据已是二维，因此需要BatchNorm1d
            ,nn.ReLU(inplace=True)
            ,nn.Linear(256,out_features)
            ,nn.LogSoftmax(1)
        )
        
    def forward(self,x):
        x = self.block2(self.block1(x))
        x = x.view(-1, 64*7*7)
        output = self.classifier_(x)
        return output
data = torch.ones(10,1,28,28)
net2 = MyNet2()
net2(data).shape
#torch.Size([10, 10])
#查看自己构建的网络架构和参数量
summary(net2,input_size=(10,1,28,28),depth=3,device="cpu")
# ==========================================================================================
# Layer (type:depth-idx)                   Output Shape              Param #
# ==========================================================================================
# MyNet2                                   --                        --
# ├─Sequential: 1-1                        [10, 32, 14, 14]          --
# │    └─BasicConv2d: 2-1                  [10, 32, 28, 28]          --
# │    │    └─Sequential: 3-1              [10, 32, 28, 28]          896
# │    └─BasicConv2d: 2-2                  [10, 32, 28, 28]          --
# │    │    └─Sequential: 3-2              [10, 32, 28, 28]          25,696
# │    └─MaxPool2d: 2-3                    [10, 32, 14, 14]          --
# │    └─Dropout2d: 2-4                    [10, 32, 14, 14]          --
# ├─Sequential: 1-2                        [10, 64, 7, 7]            --
# │    └─BasicConv2d: 2-5                  [10, 64, 14, 14]          --
# │    │    └─Sequential: 3-3              [10, 64, 14, 14]          18,624
# │    └─BasicConv2d: 2-6                  [10, 64, 14, 14]          --
# │    │    └─Sequential: 3-4              [10, 64, 14, 14]          37,056
# │    └─BasicConv2d: 2-7                  [10, 64, 14, 14]          --
# │    │    └─Sequential: 3-5              [10, 64, 14, 14]          37,056
# │    └─MaxPool2d: 2-8                    [10, 64, 7, 7]            --
# │    └─Dropout2d: 2-9                    [10, 64, 7, 7]            --
# ├─Sequential: 1-3                        [10, 10]                  --
# │    └─Linear: 2-10                      [10, 256]                 803,072
# │    └─BatchNorm1d: 2-11                 [10, 256]                 512
# │    └─ReLU: 2-12                        [10, 256]                 --
# │    └─Linear: 2-13                      [10, 10]                  2,570
# │    └─LogSoftmax: 2-14                  [10, 10]                  --
# ==========================================================================================
# Total params: 925,482
# Trainable params: 925,482
# Non-trainable params: 0
# Total mult-adds (M): 396.55
# ==========================================================================================
# Input size (MB): 0.03
# Forward/backward pass size (MB): 14.09
# Params size (MB): 3.70
# Estimated Total Size (MB): 17.82
# ==========================================================================================

这是小型数据集不适用于经典架构，而必须自建架构的情况。如果是面对大型数据集，我们通常都会将其处理为类似于ImageNet的形式（224x224x3），先用一些深层架构进行尝试，再根据实际的情况使用深层架构的全部或一部分内容。如果需要删除层，则建议直接从经典架构中提取出需要的部分来组合，如果是要增加层，则可以使用nn.Sequential打包现有架构和新增的层。当然，我们需要谨慎考虑才能决定是否要在深层架构上继续增加层，因为在较大的数据集上、尤其是真实照片上调用较大的模型时，训练成本毫无疑问是非常昂贵的。如果我们真的必须增加层，或者在有限的计算资源下训练深层神经网络，那我们可以考虑使用“迁移学习”技术，也叫做“预训练的技术”。

2.3 模型的预训练/迁移学习

大多数情况下，我们能够用于训练模型的算力和数据都很有限，要完成一个大型神经网络的训练非常困难，因此我们希望能够尽量重复利用已经训练好的神经网络以节约训练和数据资源。如果我们在执行预测任务时，能够找到一个曾经执行过相似任务、并被训练得很好的大型架构，那我们就可以使用这个大型架构中位置较浅的那些层来帮助我们构筑自己的网络。借用已经训练好的模型来构筑新架构的技术就叫做“迁移学习”（transfer learning），也叫做预训练（pre-train）。预训练是我们训练大型模型时、用于降低数据需求以及加快训练速度的关键技术之一。

我们究竟如何借用已经训练好的模型架构呢？答案是借用训练好的模型上的权重。之前我们基于经典架构构建自己的架构时，是直接将经典架构中的结构本身复制一份，再在前后增加我们希望增加的层，这个过程中的经典架构并没有被训练过，所以全部层在训练时都得初始化自己的参数、从0开始训练。但在迁移学习中，我们要复用的是一个已经训练好的架构，包括它的架构本身以及每层上的权重。如下图所示，我们沿用现存架构上的前三个隐藏层以及它们的权重，并在这三个隐藏层后再加入两个我们自定义的层，以此来构筑新的架构。当我们在训练时，我们有两种选择：

1）将迁移层上的权重作为初始化工具（Initialization tool）：将迁移层的权重作为新架构的初始化权重，在此基础上对所有层进行训练，给模型指一条“明路”。在最严谨的文献中，借用原始架构权重，并对所有层进行再训练的流程被称为“预训练”。
2）将迁移层作为固定的特征提取工具（fixed feature extractor）：我们将迁移过来的层上的权重“固定”起来，不让这些权重受到反向传播等过程的影响，而让它们作为架构中的“固定知识”被一直使用。相对的，我们自己添加的、或我们自己选择的层则可以像普通的网络架构一样初始化参数并参与训练，并在每一次迭代中逐渐找到适合自己的权重。在最严谨的文献中，这个流程被称为“迁移学习”。

这样做有什么意义呢？对神经网络来说，它所学到的知识和能够做出的判断都被储存在权重当中（我们保存模型时，也是在保存模型的权重），因此保留权重，就是保留了之前的架构已经学会的东西。在任意深层神经网络或卷积网络中，接近输入层的层所提取的信息都是较为浅层的信息，接近输出层的层所提取的信息都是深层的信息，因此我们可以认为浅层中的权重可以帮助模型建立一些有用的“常识”，而深层中的权重则可以帮助模型进行具体任务的判断。在迁移学习中，我们总是利用现存架构上较浅的部分的层，来为新架构增加一些“基础知识”。当我们需要执行的任务与原始架构执行的任务有相似之处时，这些“基础知识”可以为新架构提供很好的训练基础。这个行为相当于为新架构引入了一位名师，比起从0开始无头苍蝇一样地学习，让名师指路、再自己学习，毫无疑问是效率更高、速度更快的学习方式。因此，我们通常期待迁移学习能够大量降低模型的训练时间，即便不能，它也能够大量降低我们需要的训练数据。

然而，迁移学习的使用条件是不容忽视的。在使用迁移学习时，必须要注意以

[CODIlity]LESSON1&LESSON2

Lesson1

A binary gap within a positive integer N is any maximal sequence of consecutive zeros that is surrounded by ones at both ends in the binary representation of N.

For example, number 9 has binary representation 1001 and contains a binary gap of length 2. The number 529 has binary representation 1000010001 and contains two binary gaps: one of length 4 and one of length 3. The number 20 has binary representation 10100 and contains one binary gap of length 1. The number 15 has binary representation 1111 and has no binary gaps. The number 32 has binary representation 100000 and has no binary gaps.

Write a function:

class Solution public int solution(int N);

that, given a positive integer N, returns the length of its longest binary gap. The function should return 0 if N doesn't contain a binary gap.

For example, given N = 1041 the function should return 5, because N has binary representation 10000010001 and so its longest binary gap is of length 5. Given N = 32 the function should return 0, because N has binary representation '100000' and thus no binary gaps.

Write an efficient algorithm for the following assumptions:

N is an integer within the range [1..2,147,483,647].

Copyright 2009–2022 by Codility Limited. All Rights Reserved. Unauthorized copying, publication or disclosure prohibited.

Answer:

def solution(N):
    # write your code in Python 3.6
    or2=0
    while N>=pow(2,or2):
        or2=or2+1
    or2=or2-1
    #or2 is the maximal order of 2
    if or2==0:
        return 0
    i=or2
    n=N
    result=0
    result_temp=0
    while n>0:
        while i>=0 and n>=pow(2,i):
            n=n-pow(2,i)
            result_temp = 0
            i=i-1
            #print("n=",n,"while i=",i)
        while n<pow(2,i) and i>=0:
            result_temp = result_temp + 1
            i=i-1
            #print("result_temp=",result_temp,"while i=",i)
        if n>=pow(2,i):
            if result<result_temp:
                result = result_temp
                #print("result=",result,"while i=",i)
    return result

Lesson2:

Task1:

An array A consisting of N integers is given. Rotation of the array means that each element is shifted right by one index, and the last element of the array is moved to the first place. For example, the rotation of array A = [3, 8, 9, 7, 6] is [6, 3, 8, 9, 7] (elements are shifted right by one index and 6 is moved to the first place).

The goal is to rotate array A K times; that is, each element of A will be shifted to the right K times.

Write a function:

def solution(A, K)

that, given an array A consisting of N integers and an integer K, returns the array A rotated K times.

For example, given
A = [3, 8, 9, 7, 6] K = 3
the function should return [9, 7, 6, 3, 8]. Three rotations were made:
[3, 8, 9, 7, 6] -> [6, 3, 8, 9, 7] [6, 3, 8, 9, 7] -> [7, 6, 3, 8, 9] [7, 6, 3, 8, 9] -> [9, 7, 6, 3, 8]
For another example, given
A = [0, 0, 0] K = 1
the function should return [0, 0, 0]

Given
A = [1, 2, 3, 4] K = 4
the function should return [1, 2, 3, 4]

Assume that:

N and K are integers within the range [0..100];
each element of array A is an integer within the range [−1,000..1,000].

In your solution, focus on correctness. The performance of your solution will not be the focus of the assessment.

Answer:

# you can write to stdout for debugging purposes, e.g.
# print("this is a debug message")

def solution(A, K):
    # write your code in Python 3.6
    if len(A)==0:
        return A
    kk = K % len(A) 
    # A[0] --> solu[kk]
    if kk==0:
        return A
    i=len(A)-kk
    B=[A[i]]
    i=i+1
    while i<len(A):
        B.append(A[i])
        i=i+1
    i=0
    while i<len(A)-kk:
        B.append(A[i])
        i=i+1
    return B

Task2:

A non-empty array A consisting of N integers is given. The array contains an odd number of elements, and each element of the array can be paired with another element that has the same value, except for one element that is left unpaired.

For example, in array A such that:
A[0] = 9 A[1] = 3 A[2] = 9 A[3] = 3 A[4] = 9 A[5] = 7 A[6] = 9

the elements at indexes 0 and 2 have value 9,
the elements at indexes 1 and 3 have value 3,
the elements at indexes 4 and 6 have value 9,
the element at index 5 has value 7 and is unpaired.

Write a function:

def solution(A)

that, given an array A consisting of N integers fulfilling the above conditions, returns the value of the unpaired element.

For example, given array A such that:
A[0] = 9 A[1] = 3 A[2] = 9 A[3] = 3 A[4] = 9 A[5] = 7 A[6] = 9
the function should return 7, as explained in the example above.

Write an efficient algorithm for the following assumptions:

N is an odd integer within the range [1..1,000,000];
each element of array A is an integer within the range [1..1,000,000,000];
all but one of the

Answer:

在大数据集上表现不够好，综合得分66%

def solution(A):
    # write your code in Python 3.6
    if len(A)==0:
        print("The array should be nonempty!")
        return 0
    if len(A)%2==0:
        print("The lenth of the array should be odd!")
        return 0
    B=[A[0]]
    N=len(A)
    for i in range(1,len(A)):
        #当B里没有与A[i]匹配的元素时，将A[i]加入B
        #print("now dealing with A[i]=",A[i])
        tt=0
        for j in range(len(B)):
            if B[j]==A[i]:
                tt=1
                break
        if tt==0:
            B.append(A[i])
        else:
            del B[j]
        #print("now B=",B)
    if len(B)!=1:
        print("Error exits!")
    return B[0]

后来学了新招：直接用异或……

# you can write to stdout for debugging purposes, e.g.
# print("this is a debug message")

def solution(A):
    # write your code in Python 3.6
    a=0
    for i in range(len(A)):
        a=a^A[i]
    return a

成功了……

以上是关于Lesson 17.7&17.8&17.9&17.10 调用经典框架&基于resnet与vgg的自建架构&基于普通卷积层和池化层的自建架构&有监督的预训的主要内容，如果未能解决你的问题，请参考以下文章

0301001_Lesson1&2

1001001_Lesson1&2

第十七章委托

PoEdu - Windows阶段班 Po学校Lesson006_线程_线程的启动到消亡 &线程状态 & 线程安全 & CONTEXT结构体 & 令牌锁

Level 1-Lesson 9. Excel & Data Tables

自测之Lesson15：TCP&UDP网络编程