数据结构与算法——堆的基本存储

Posted 2023-03-31 bit..

目录

一、概念及其介绍

二、适用说明

三、结构图示

四、Java 实例代码

五.堆和栈的区别

---

一、概念及其介绍

堆(Heap)是计算机科学中一类特殊的数据结构的统称。

堆通常是一个可以被看做一棵完全二叉树的数组对象。

堆满足下列性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值。
• 堆总是一棵完全二叉树。

二、适用说明

堆是利用完全二叉树的结构来维护一组数据，然后进行相关操作，一般的操作进行一次的时间复杂度在 O(1)~O(logn) 之间，堆通常用于动态分配和释放程序所使用的对象。

若为优先队列的使用场景，普通数组或者顺序数组，最差情况为 O(n^2)，堆这种数据结构也可以提高入队和出队的效率。

三、结构图示

二叉堆是一颗完全二叉树，且堆中某个节点的值总是不大于其父节点的值，该完全二叉树的深度为 k，除第 k 层外，其它各层 (1～k-1) 的结点数都达到最大个数，第k 层所有的结点都连续集中在最左边。

其中堆的根节点最大称为最大堆，如下图所示：

我们可以使用数组存储二叉堆，右边的标号是数组的索引

 

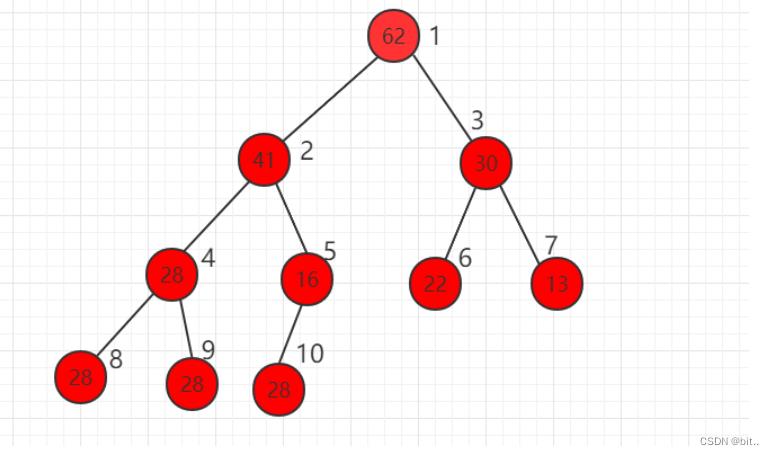
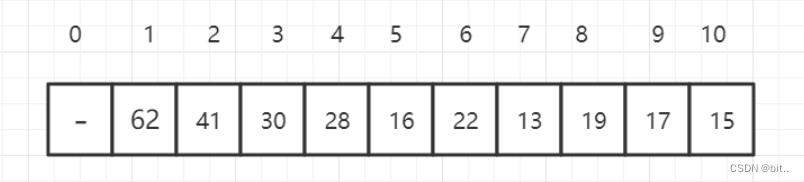
假设当前元素的索引位置为 i，可以得到规律：

parent(i) = i/2（取整）
left child(i) = 2*i
right child(i) = 2*i +1

 四、Java 实例代码

package runoob.heap;

/**
 * 堆定义
 */
public class MaxHeap<T> 
    private T[] data;
    private int count;
    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    public MaxHeap(int capacity)
        data = (T[])new Object[capacity+1];
        count = 0;
    
    // 返回堆中的元素个数
    public int size()
        return count;
    
    // 返回一个布尔值, 表示堆中是否为空
    public boolean isEmpty()
        return count == 0;
    
    // 测试 MaxHeap
    public static void main(String[] args) 
        MaxHeap<Integer> maxHeap = new MaxHeap<Integer>(100);
        System.out.println(maxHeap.size());
    

五.堆和栈的区别

• 栈Stack：是私有的，每创建一个线程就会创建一个栈，栈中存放数据为当前线程中局部基本类型的数据，（java中定义的八种基本类型：boolean、char、byte、short、int、long、float、double），非基本类型的对象在JVM栈上仅存放一个指向堆上的地址
• 堆Heap ：JVM用来存储对象实例以及数组值的区域，可以认为Java中所有通过new创建的对象的内存都在此分配，Heap中的对象的内存需要等待GC进行回收

数据结构与算法

一、数据结构

1.理解常见数据结构的特点，以及他们在不同场景下使用的优缺点

2.理解数组、字符串的存储原理，并熟练应用他们解决问题

3.理解二叉树、栈、队列、哈希表的基本结构和特点，并可以应用它解决问题

4.了解图、堆的基本结构和使用场景

二、算法

三、手动实现前端轮子