[Java]深入剖析常见排序
Posted Node_Hao
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[Java]深入剖析常见排序相关的知识,希望对你有一定的参考价值。

专栏简介 :java语法及数据结构
题目来源:leetcode,牛客,剑指offer
创作目标:从java语法角度实现底层相关数据结构,达到手撕各类题目的水平.
希望在提升自己的同时,帮助他人,,与大家一起共同进步,互相成长.
学历代表过去,能力代表现在,学习能力代表未来!
目录
前言
排序算法在数据结构中属于操作性较强的一种,深入学习不仅能加深我们对算法优化的理解,还能培养我们在实际问题中找出最优算法的能力,因此我们有必要系统的学习并总结一下常见的基本排序.
一> 概念
1.1 排序:
排序就是将一串记录中关键字的大小按递增或递减排列起来的操作,本文中所讲排序都是默认升序(非降序)且原地排序(in place sort)指不借助外存仅在内存中排序.
假如我们电脑内存只有1G,但需求是排序100G的数据,那么肯定不能在电脑内存中排序,需要借助硬盘.
1.2 稳定性:
两个相等的数据经过排序后,其相对位置不发生变化,我们称其为稳定排序.
注意:稳定排序可以变得不稳定,但本身不稳定的排序无法使其稳定.

1.3 应用:
二> 常见排序总览

三> 直接插入排序(Insertion Sort)
3.1 算法描述:
- 步骤1:假定第一个元素已经有序从第二个元素开始比较,
- 步骤2:先将第二个元素存入临时变量tmp,然后从后向前扫描.
- 步骤3:若第一个元素大于tmp,则让第一个元素移到下一位.
- 步骤4:重复步骤3直到找到小于等于tmp的元素.
- 步骤5:将tmp插入该元素后面,若该元素下标小于0,直接插入0位置.
3.2 动图演示:
3.3 代码描述:
public static void insertSort1(int[] array) for (int i = 1; i < array.length; i++) int tmp = array[i]; int j = i-1; for (; j >=0 ; j--) if (array[j]>tmp) array[j+1] = array[j]; else //只要J在回退过程中遇到比tmp小的元素,就可以停止了. break; //J回退到了小于0的地方的情况下 array[j+1] = tmp;3.4 算法分析:
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
Tips:插入排序最大的优势是排序相对有序的序列,其时间复杂度可以优化为O(N),常用于其他排序的优化.(假设序列为:2 4 5 10 18 12 只需排序18 12 前面的一概不管)
四> 希尔排序(Shell Sort)
假如我们有10000个数据需要排序,使用直接插入排序需要排序10000x10000 = 1亿次,但如果将这10000个数据分成100组,分别每组进行排序 .那么只需排序100x100 = 10000次.由此可见分组插入排序的思想大大简化了排序的时间复杂度.希尔排序也是在此基础上衍生的.
4.1 算法描述:
然而希尔排序的分组并不是简单的将一组数据均分,而是要满足最小增量原则但最终的组数一定要等于1,例如一组数据有15个元素,我们可以先分为5组排序依次排序,再分为3组依次排序,最后分为1组排序.
- 步骤1:初始组数为数组初始长度,每次递减一半.
- 步骤2:将分好的组直接插入排序
- 步骤3:重复上述操作直到分组为1.
4.2 动图演示:
4.3 代码描述:
public static void shellSort(int[]arr) int n = arr.length int gap = n; while (gap>1) gap/=2;//保证gap最后一次一定是1 for(int i = 0;i < n - gap;i++) int end = i; int tmp = arr[end + gap]; while(end >= 0) if(arr[end] > tmp] arr[end + gap] = arr[end]; end-=gap; else break; arr[end + gap] = tmp;4.4 算法分析:
- 时间复杂度:O(N^1.3-1,5)
- 空间复杂度:O(1)
- 不稳定
Tips:快速判断一个排序是否稳定,看交换元素时是否跳跃.(由于制造素数的分组需要特殊函数,所以本次代码中的分组方式以除以2来替代,时间复杂度不一定满足理想情况.)
五> 选择排序(Selection Sort)
5.1 算法描述:
- 步骤1: i 记录首元素下标,j 记录i+1元素下标.
- 步骤2:二者比较若array[j]<array[i],二者交换.
- 步骤3:否则j++,重复上述步骤,直到j>array.length.
- 步骤3:i++,j++重复上述步骤.直到i>array.length.
5.2 动图演示:
5.3 代码描述:
public static void swap(int[] array,int i,int j) int tmp = array[i]; array[i] = array[j]; array[j] = tmp; public static void selectSort1(int[] array)//优化算法 for (int i = 0; i < array.length; i++) int minIndex = i; for (int j = i+1; j < array.length ; j++) if (array[j]<array[minIndex]) minIndex = j; swap(array,i,minIndex);5.4 算法分析:
- 时间复杂度:O(N^2).
- 空间复杂度:O(1) .
- 稳定性:不稳定.
六> 堆排序 (Heap Sort)
6.1 算法描述:
- 步骤1:建堆(大根堆).
- 步骤2:0下标记录为首元素,end下标记录为尾元素.(end = array.length).
- 步骤3:swap(0,end),然后向下调整(shiftDown)为大根堆,end--
- 步骤4:重复2-3步骤直到end=0.
Tips:堆排序之所以要创建为大根堆再不断的交换首尾元素是因为,如果我们创建为小根堆只能保证堆顶元素最小,却无法保证左右孩子的大小与其下标对应.而不断的交换大根堆的首尾元素一定能够保证最大的元素在末尾.
6.2 动图演示:
6.3 代码描述:
public static void heapSort(int[] array) //1.创建大根堆 O(N) createHeap(array); int end = array.length - 1; //2.交换调整 O(N)*O(logN) while (end > 0) swap(array, 0, end); shiftDown(array, 0, end); end--; public static void createHeap(int[] array) for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) shiftDown(array, parent, array.length); public static void shiftDown(int[] array, int parent, int len) int child = 2 * parent + 1; while (child < len) if (child + 1 < len && array[child] < array[child + 1]) child++;//确保child下标是左右孩子最大值. if (array[parent] < array[child]) swap(array, parent, child); parent = child; child = child * 2 + 1; else break;6.4 算法分析:
- 时间复杂度:O(N*logN).
- 空间复杂度:O(1).
- 稳定性:不稳定.
七> 冒泡排序(Bubb;e Sort)
7.1 算法描述:
冒泡排序相信大家已经非常熟悉了,本文提供优化后的冒泡排序,排序过程中当数组已经有序,那么继续排序会浪费时间,我们可以记录每次排序的状况,如果一趟排序发生交换就将flg置为true,当flg不为true时说明数组有序.,直接跳出循环即可.
7.2 动图演示:
7.3 代码描述:
public static void BubbleSort(int[] array) for (int i = 0; i < array.length - 1; i++) boolean flg = false; for (int j = i; j < array.length - 1 - i; j++) if (array[j] > array[j + 1]) swap(array, j, j + 1); flg = true; if (flg == false) break;7.4 算法分析:
- 时间复杂度:O(N^2).
- 空间复杂度:O(1).
八> 快速排序(Quick Sort)
8.1算法分析:
核心思想是分治思想,不断寻找一组数据的基准(基准左边的数据比它小右边比它大),当数据被细分到无法继续寻找基准时,整个数据已排序完毕.寻找基准的方法有很多,主流的方法是挖坑法和Hore法,绝大多数常见的笔试面试题都可使用用挖坑法,所以我们主要采用挖坑法来实现.
- 步骤1:使用left和rightfb记录数据的首尾元素下标.
- 步骤2:确定递归结束的条件为left>=right.
- 步骤3:调用找基准的函数,找到该组数据的基准pivot.
- 步骤4:用基准将数据分为左右子树继续递归.
挖坑法:顾名思义就是在数据中挖出元素再填入元素.
- 步骤1:start和end分别记录数据的首尾元素下标.
- 步骤2:以数据第一个元素为基准,由tmp记录.(相当于将第一个元素挖出)
- 步骤3:end开始从后往前寻找小于tmp的元素埋入空出的位置.(此时end被挖出)
- 步骤4:start开始从前往后寻找大于tmp的元素埋入空出的位置.
- 步骤5:重复3-4步骤,直到start == end,将tmp填入空出的中间位置.
- 步骤6:此时start/end下标就是基准的位置,返回该元素即可.
8.2 动图演示:
8.3 代码描述:
public static void quickSort(int[] array, int left, int right) if (left >= right) return; int pivot = partition(array, left, right); quickSort(array, left, pivot - 1); quickSort(array, pivot + 1, right); public static int partition(int[] array, int start, int end) int tmp = array[start]; while (start < end) while (start < end && array[end] >= tmp) end--; array[start] = array[end]; while (start < end && array[start] <= tmp) start++; array[end] = array[start]; array[start] = tmp; return array[start];8.4 算法分析:
- 时间复杂度:最好情况下O(N*logN),最坏情况下O(N^2).
- 空间复杂度:最好情况下O(logN),最好情况下O(N).
- 稳定性:不稳定.
Tips:如果数据是有序的假设为[1,2,3,4,5,],那么就会出现如下图所示单分支的情况,由于递归占用栈的空间,如果数据过大一定会出现栈溢出(stack over flow)的情况.所以我们需要优化快速排序找基准的方式.
8.5 算法优化(三数取中法)
假设有一组有序数据1, 2,3,4,5 使用三数取中法,找到3元素的下标与left交换,一定可以避免基准为1的情况.以下是优化版快速排序.
public static void quickSort(int[] array, int left, int right) if (left >= right) return; //找基准之前,我们先找到中间大小的值. int midValIndex = findMidValIndex(array,left,right); //交换left与中间元素的值. swap(array,left,midValIndex); int pivot = partition(array, left, right); quickSort(array, left, pivot - 1); quickSort(array, pivot + 1, right); //找中间元素 private static int findMidValIndex(int[] array,int start,int end) int minValIndex = start+((end-start)>>>1); if (array[start]<array[end]) if (array[minValIndex]>array[end]) return end; else if (array[start]<array[minValIndex]) return minValIndex; else return start; else if (array[minValIndex]>array[start]) return start; else if (array[minValIndex]<array[end]) return end; else return minValIndex; //找基准 public static int partition(int[] array, int start, int end) int tmp = array[start]; while (start < end) while (start < end && array[end] >= tmp) end--; array[start] = array[end]; while (start < end && array[start] <= tmp) start++; array[end] = array[start]; array[start] = tmp; return start;
九> 归并排序(Merge Sort)

1.准备阶段:
学习归并排序之前首先要知道如何将两个有序数组合并为一组.
public static int[] mergeTwoArray(int[] array1,int[] array2)
if(array1==null||array2==null)
throw new RuntimeException("传入异常");
int[] tmp = new int[array1.length+ array2.length];
int k = 0;//记录k的下标
int s1 = 0;
int e1 = array1.length-1;
int s2 = 0;
int e2 = array2.length-1;
while (s1<=e1&&s2<=e2)
if(array1[s1]<=array1[s2])
tmp[k++] = array1[s1++];
else
tmp[k++] = array2[s2++];
while (s1<=e1)
tmp[k++] = array1[s1++];
while (s2<=e2)
tmp[k++] = array2[s2++];
return tmp;
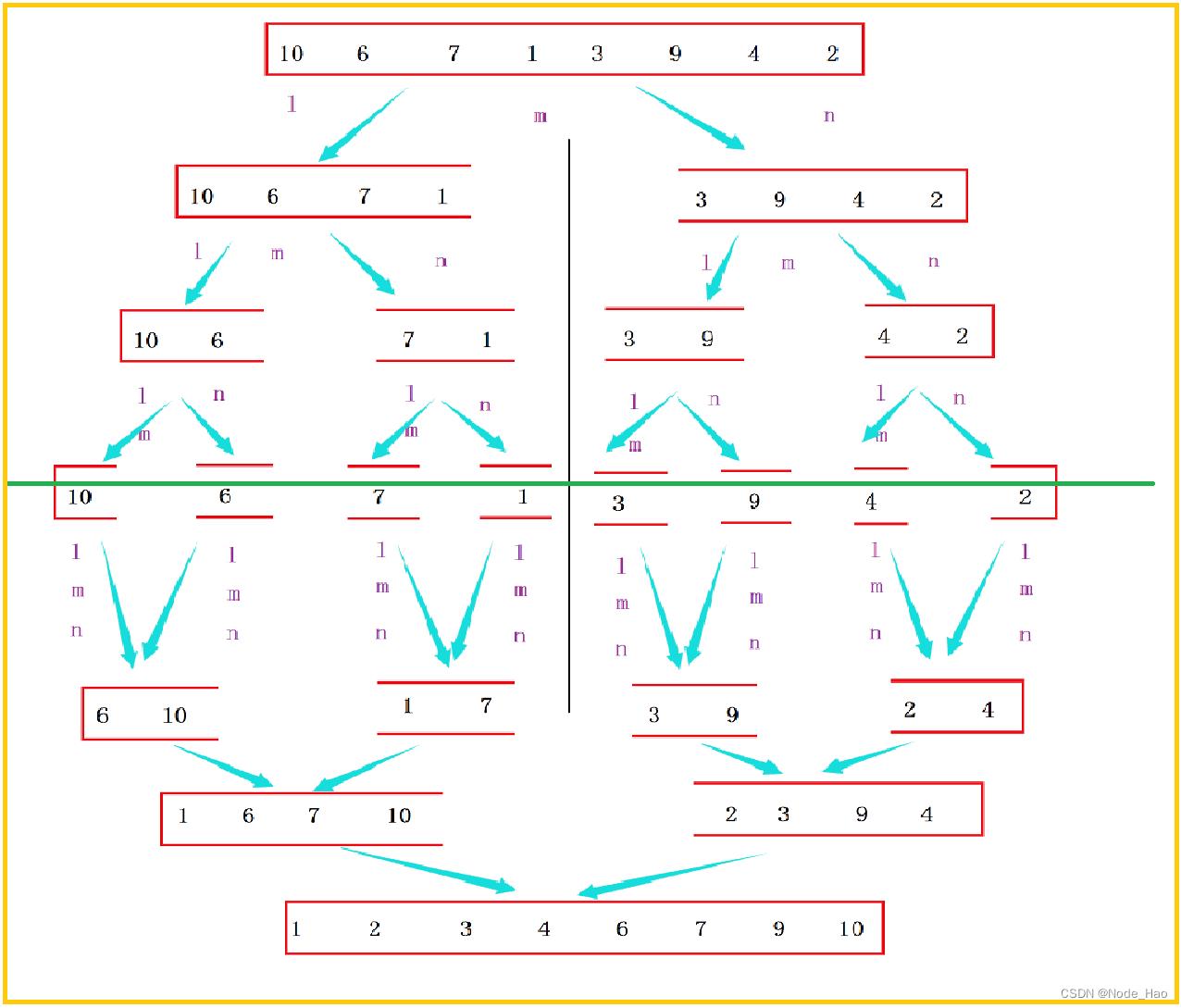
2.递归写法:
递归写法采用分治思想,将一串数据用类似二叉树的结构不断递归
- 步骤1 :递归的结束条件是left>=rigth,
- 步骤2: 每次遍历完左右子树就运用合并两个有序数组将其合并一次,
- 步骤3: 当递归结束后数组也趋于有序.
算法分析:
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:稳定(合并有序数组时有一段代码if(array[s1]<=array[s2])
tmp[k++] = array[s1++];意味着s1中等于s2的元素永远在s2之前.
public static void mergeSort(int[]array)
mergeInternal(array,0, array.length-1);
//递归法
public static void mergeInternal(int[] array,int left,int right)
if(left>=right)
return;
int mid = left + ((right - left) >>> 1);
mergeInternal(array, left, mid);
mergeInternal(array, mid + 1, right);
mergeArray(array, left, mid, right);
public static void mergeArray(int[] array,int left,int mid,int right) //合并两个有序数组
if(array==null)
throw new RuntimeException("传入异常");
int[] tmp = new int[right-left+1];
int k = 0;
int s1 = left;
int s2 = mid+1;
int e1 = mid;
int e2 = right;
while (s1<=e1&&s2<=e2)
if(array[s1]<=array[s2])
tmp[k++] = array[s1++];
else
tmp[k++] = array[s2++];
while (s1<=e1)
tmp[k++] = array[s1++];
while (s2<=e2)
tmp[k++] = array[s2++];
//拷贝数组
for(int i = 0;i<tmp.length;i++)
array[i+left] = tmp[i];
3.非递归写法:
常见可视化化动图都是采用非递归写法,将数组拆分为每组一个元素的小数组,组与组之间进行有序合并,随着组内元素的增加合并的范围也更大.核心思想就是分治归并,两倍两倍的合并排序.

//非递归法
public static void mergeSort2(int[]array)
int nums = 1;//初始每组数据的个数
while (nums< array.length)
//数组每次都要遍历,确定要归并的区间
for (int i = 0; i < array.length; i+=nums*2)
int left = i;
int mid = left+nums-1;
if(mid>= array.length)
mid = array.length-1;
int right = mid+nums;
if(right>= array.length)
right = array.length-1;
//下标确定之后,进行合并
mergeArray(array,left,mid,right);
nums*=2;
public static void mergeArray(int[] array,int left,int mid,int right) //合并两个有序数组
if(array==null)
throw new RuntimeException("传入异常");
int[] tmp = new int[right-left+1];
int k = 0;
int s1 = left;
int s2 = mid+1;
int e1 = mid;
int e2 = right;
while (s1<=e1&&s2<=e2)
if(array[s1]<=array[s2])
tmp[k++] = array[s1++];
else
tmp[k++] = array[s2++];
while (s1<=e1)
tmp[k++] = array[s1++];
while (s2<=e2)
tmp[k++] = array[s2++];
//拷贝数组
for(int i = 0;i<tmp.length;i++)
array[i+left] = tmp[i];
十> 计数排序(Counting Sort)
计数排序的核心是: 将输入数据转化为下标(键),储存在额外开辟的数组中,作为一种线性时间复杂度的排序,计数排序要求排序数据必须是确定定范围的整数.因此它只能对整数进行排序.
10.1 算法描述:
- 步骤1: 找出待排序数组中,最大和最小的元素.
- 步骤2: 创建新数组统计元素数组中每个数据出现的次数.
- 步骤3: 遍历新数组中每个元素,存入到原来数组中.
Tips:待排序数据不一定是1-n,有可能是900-999,此时我们不可能创建大小为1000的数组,所以找出最大最小的元素可以确定创建多大的数组,并且步骤三中存入原数组时,需要让新数组中每个元素加上最小值,这样才能对应到原数组.
10.2 动图演示:
10.3 代码描述:
public static void countingSort(int[] array) //先用擂台原理找到maxVal和minVal int maxVal = array[0]; int minVal = array[0]; for (int i = 0; i < array.length; i++) if (maxVal < array[i]) maxVal = array[i]; if (minVal > array[i]) minVal = array[i]; int[] count = new int[maxVal - minVal + 1]; //统计Array数组中,每个数据出现的次数 for (int i = 0; i < array.length; i++) int index = array[i]; //为了空间合理使用 这里需要index减去最小值 count[index - minVal]++; //接下来只需遍历计数数组即可 int indexArray = 0; for (int i = 0; i < count.length; i++) while (count[i] > 0) //一定要加minVal array[indexArray] = i + minVal; count[i]--; indexArray++;10.4 算法分析:
假设数组有k个元素,那么其时间复杂度为O(n+k),由于计数排序不是比较排序所以理想情况下它比任何比较排序都快,但对于数据较大的情况需要更大的时间和内存.
- 时间复杂度:O(n+k).
- 空间复杂度:O(k).
总结
以上就是常见排序的所有内容,之所以放在数据结构靠后的位置是因为部分排序涉及到二叉树递归和堆的内容,由此可见数据结构之间的关联性很强.码字不易,记得三连哦!!

深入剖析原理!mysql升序排序添加条件
Maven权威指南
首先,本书适合所有Java程序员阅读。由于自动化构建、依赖管理等问题并不只存在于Java世界,因此非Java程序员也能够从该书中获益。无论你是从未接触过Maven、还是已经用了Maven很长时间,亦或者想要扩展Maven,都能从本书获得有价值的参考建议。其次,本书也适合项目经理阅读,它能帮助你更规范、更高效地管理Java项目。
Maven学习目录:
赶时间的朋友可以直接跳到文末获得免费领取方式!
- 第1章对Maven做了简要介绍,通过一些程序员熟悉的例子介绍了Maven是什么,为什么需要Maven。建议所有读者都阅读以获得一个大局的印象。
- 第2~3章是对Maven的一个入门介绍,这些内容对初学者很有帮助,如果你已经比较熟悉Maven,可以跳过。
- 第4章介绍了本书使用的背景案例,后面的很多章节都会基于该案例展开,因此建议读者至少简单浏览一遍。
- 第5~8章深入阐述了Maven的核心概念,包括坐标、依赖、仓库、生命周期、插件、继承和多模块聚合,等等,每个知识点都有实际的案例相佐,建议读者仔细阅读。
- 第9章介绍使用Nexus建立私服,如果你要在实际工作中使用Maven,这是必不可少的。
- 第10~16章介绍了一些相对高级且离散的知识点,包括测试、持续集成与Hudson、Web项目与自动化部署、自动化版本管理、智能适应环境差异的灵活构建、站点生成,以及Maven的Eclipse插件m2eclipse,等等。读者可以根据自己实际需要和兴趣选择性地阅读。
- 第17~18章介绍了如何编写Archeype和Maven插件。一般的Maven用户在实际工作中往往不需要接触这些知识,如果你需要编写插件扩展Maven,或者需要Archetype维护自己的项目骨架以方便团队开发,那么可以仔细阅读这两章的内容。
第一章:maven简介
- 何为maven
- 为什么需要maven
- maven与极限编程
- 被误解的maven

第二章:maven的安装和配置
- 在Windows上安装maven
- 在基于UNIX的系统上安装maven
- 安装目录分析
- maven安装最佳实践

第三章:maven使用入门
- 编写POM
- 打包和运行
- m2eclipse简单使用
- NetBeans Maven插件简单使用

第四章:背景案例
第五章:坐标和依赖
第六章:仓库
第七章:生命周期和插件
第八章:聚合与继承
第九章:使用Nexus创建私服
第十章:使用Maven进行测试
第十一章:使用Hudson进行持续集成
第十二章:使用Maven构建Web应用
第十三章:版本管理
第十四章:灵活的构建
第十五章:生成项目站点
第十六章:m2eclipse
第十七章:编写maven插件
第十八章:Archetype

总结
在清楚了各个大厂的面试重点之后,就能很好的提高你刷题以及面试准备的效率,接下来小编也为大家准备了最新的互联网大厂资料。

.(img-c915HIuv-1626705293448)]
[外链图片转存中…(img-rQakKfcr-1626705293449)]
以上是关于[Java]深入剖析常见排序的主要内容,如果未能解决你的问题,请参考以下文章