用js来实现那些数据结构14（树02-AVL树）

Posted 2020-11-02 Zaking

　　在使用二叉搜索树的时候会出现 一个问题，就是树的一条分支会有很多层，而其他的分支却只有几层，就像下面这样：

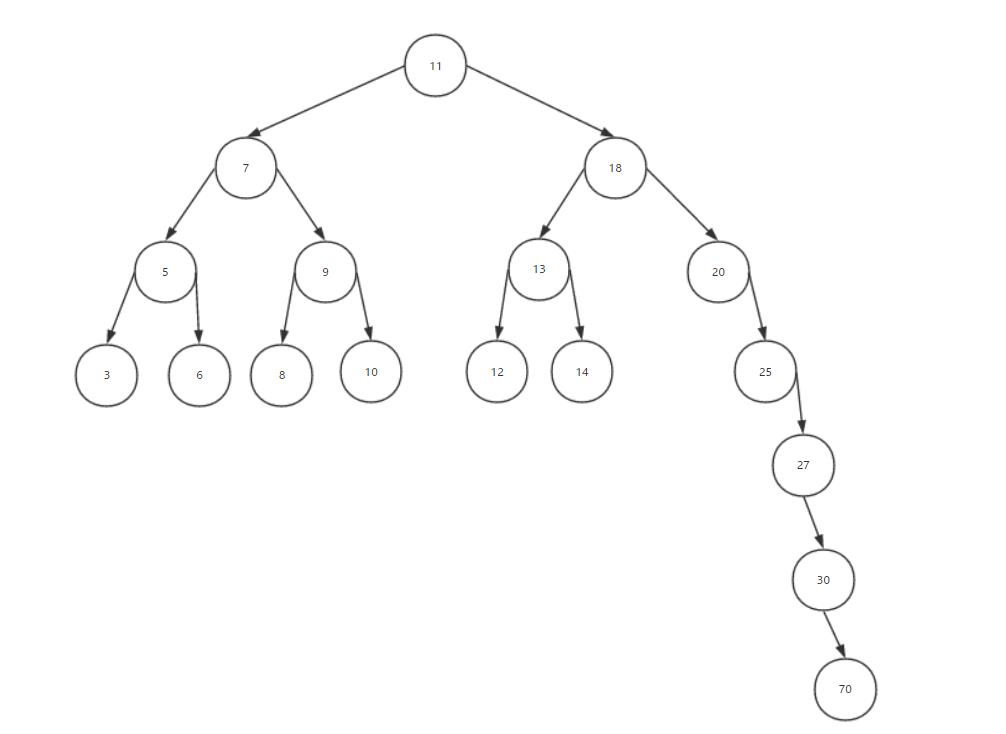
　　如果数据量够大，那么我们在某条边上进行增删改查的操作时，就会消耗大量的时间。我们花费精力去构造一个可以提高效率的结构，反而事与愿违。这不是我们想要的。所以，我们需要另外一种树来解决这样的问题，那就是自*衡二叉搜索树--Adelson-Velskii-Landi（AVL）。什么意思呢？就是说这种树的任何一个节点左右两侧子树的高度之差最多为1。也就是说这种树会在添加或删除节点时尽量试着成为一棵完全树。

　　自*衡二叉搜索树和二叉搜索树的实现几乎是一模一样的，唯一的区别就在于每次在插入或者删除节点的时候，我们需要检测它的*衡因子（因为只有再插入或者删除的时候才有可能会影响到树的*衡性）。如果有需要，那么就将其逻辑应用于树的自*衡。

　　首先我们需要知道这个*衡因子是如何计算的。*衡因子的计算是来自于每个节点的右子树高度（hr）和左子树高度（hl）的差值， 该值应为0，1，-1.如果不是这三个值，那么说明需要*衡该AVL树。这就是*衡因子的简单计算方式。什么意思呢？

 　　我们以上图为例，根节点11的*衡因子6 - 3 = 3。左侧子节点7的*衡因子是2 - 2 = 0；右侧子节点18的*衡因子就是5 - 2 = 3；节点70的*衡因子是0，要记住所有的叶节点（外部节点）的*衡因子都是0。因为叶节点没有子节点。还有一点一定要注意。我们所计算的*衡因子，是该节点的左右子树的高度。

　　我们学会了如何去计算*衡因子，那么我们下面进行一项及其重要的仪式......噢，sorry。是及其重要的知识——旋转。

　　在开始讲解旋转之前，我们先来点开胃菜。看看我们插入子节点后，导致该树不*衡的可能的情况有哪些。我会画几个图，以便大家看得仔细透彻。

　　

 

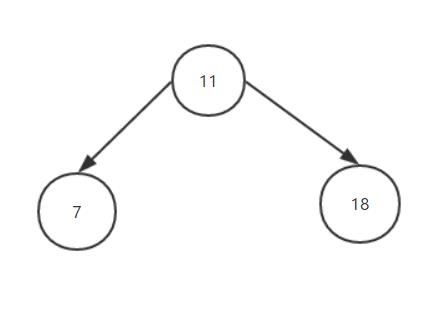
　　首先，我们以上面这张图（截取前面树结构的一部分）作为初始的树，这棵树绝对一定必然是*衡的。大家都没意见吧。那么RR,LL,RL,LR是什么意思呢？那么我们继续往下看。

　　第一种情况：RR。

　　　　我们在18的右侧子节点再加一个节点20，右侧是要加入比父节点大的值的。

 

 

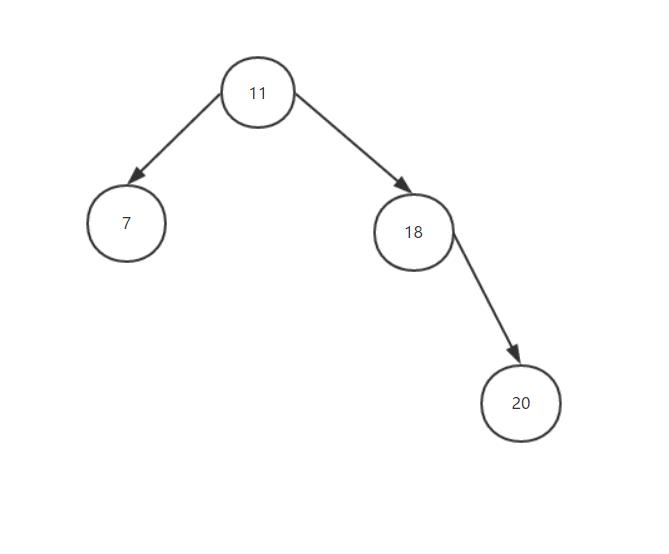
　　　　在我们加入了一个节点20之后，我们发现这棵树还是*衡的！唉？不对啊，跟我想要的结果好像不太一样。我再加一个节点试试？

 

 

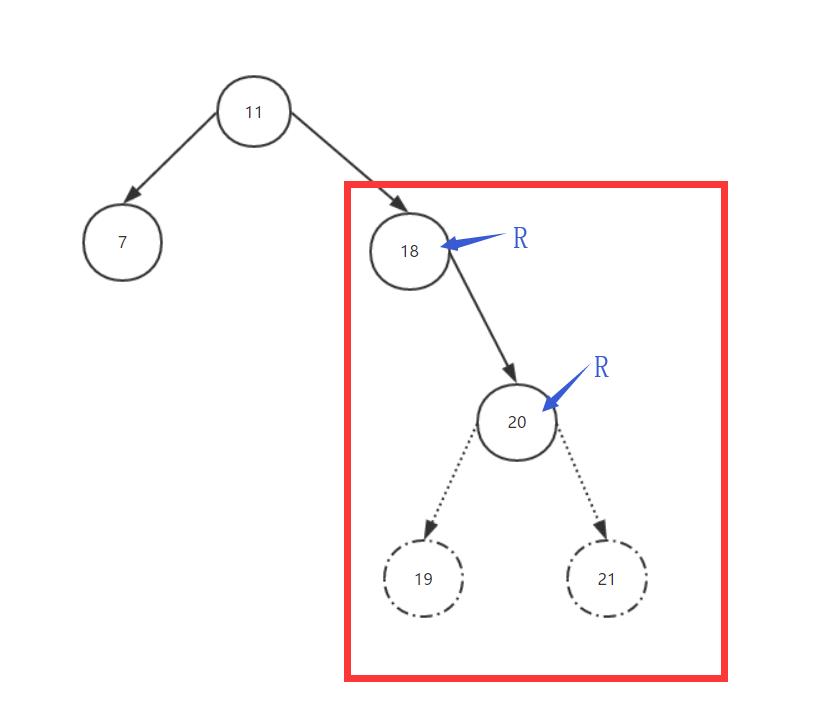
　　　　嗯......现在绝壁不*衡了。那么我们来看看怎么回事。在加入节点21（19）后，11节点左侧子树的深度是1，而右侧子树的深度是1，2，3。是3没错。那么1-3等于-2。嗯，十以内加减法应该不会算错。我们确定在节点18后面加入了两个右侧（R）节点后，这棵树就不*衡了。而现在有一个重要的问题。就是是哪一棵子树导致这棵树不*衡的呢？是在我们加入节点21（19）之后，也就是上图我们用小圈圈诅咒它的那一部分。那么我们可以用一句话来描述，我们在该树右侧子节点的右侧子节点加入了一个右侧子节点(如果加入的是左侧子节点也是一样的)之后，导致了该树的不*衡，所以我们这时候需要去操作也就是旋转右侧的子节点也就是18节点，来使这颗自*衡树来自*衡。换句话说，如果我们加入了一个节点（或者删除了一个节点），导致了我们整颗树的不*衡，那么我们首先要找到最*的不*衡的树来进行调整。

　　　　上面RR情况的我分别加入了19，和21两个字节点，要说明一下，这两个子节点是为了更为清晰的告诉大家在root的右节点的右节点下，无论插入的是左节点还是右节点都属于RR的情况。下同。在具体旋转的时候会给大家详细介绍。

　　　　换句话说，我们判断在增删节点的时候是否会导致不*衡的情况，由插入节点的前两个父节点来确定！大家要注意噢！很重要！

　　　　趁热打铁，上面解释了RR的情况，那么其实下面的LL，LR，RL等情况也是一样的。思路没有任何区别。但是这个时候我想打断大家一下。问大家两个问题。这两个问题的解决会为后面的学习带来极大的便利。

　　　　1、在AVL树或者其他树中，是否可以出现重复的值，比如树中已经有了一个11，我还想再加入一个11，是否允许？是否可以？

　　　　2、看上图（RR情况图），是否有可能出现除了这四种情况外的其他情况？或者说，节点的*衡因子是否可能出现大于2或者小于-2的情况？（这种情况我们要旋转树超过两次，也就超出了我们这四种情况之外。）

　　　　OK。希望大家闭上眼睛，想一想你的梦中情人，哦不对。想一想你的答案。

　　　　不卖关子了，但是我真的希望大家想一想，因为这很必要也很重要。

　　　　好吧，我开始回答第一个问题。其实在前一篇实现的树中是不允许重复的值出现的，我们可以去看一下上一篇的代码，如果相等则会覆盖。那么可能有人会问，我想要这棵树存储重复的值（当然其实这种情况出现的话大多数都是你的设计有问题。。。没有唯一标识了啊......需求还怎么实现）。那么我记得在hashMap篇中有一个解决冲突的办法，是不是可以通过链表来存储key值相同的映射呢？是否还可以使用其他的存储方式？答案比较开放。所以是否可以存放重复的值，看你的实际需求咯。

　　　　第二个问题的答案，不可能出现，因为大家一定要记住一个前提，就是我们在插入了一个导致该树不*衡的节点前，该树一定是*衡的。为什么这么说呢？因为我们的AVL树，是自*衡二叉搜索树，如果在插入之前就是不*衡的，那你告诉我你这是啥?赶紧回头看代码，有BUG了亲。

　　　　这里希望大家已经解除了心中不少的疑惑，如果还有问题，大家可以继续留言探讨。

　　　　那么我们下面继续，把其它几种情况的图示画完。

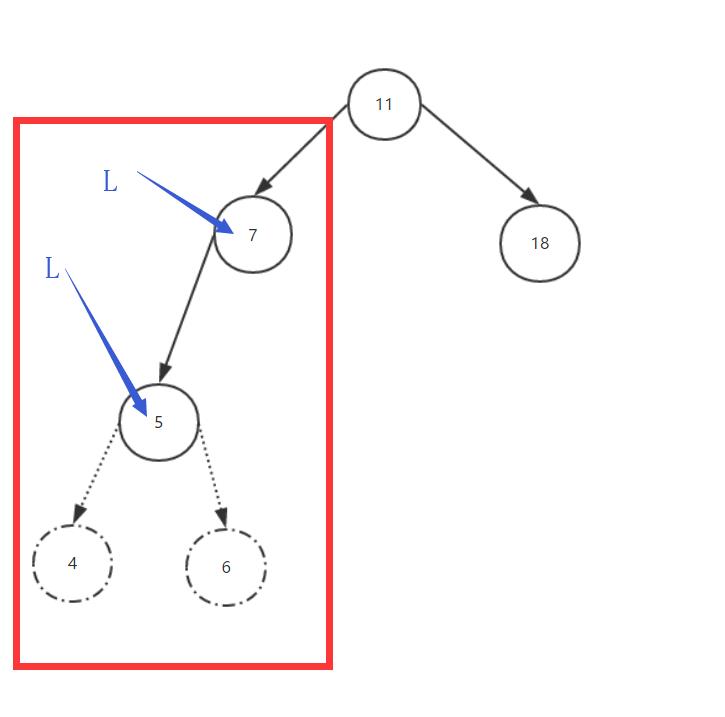
　　第二种情况：LL。

　

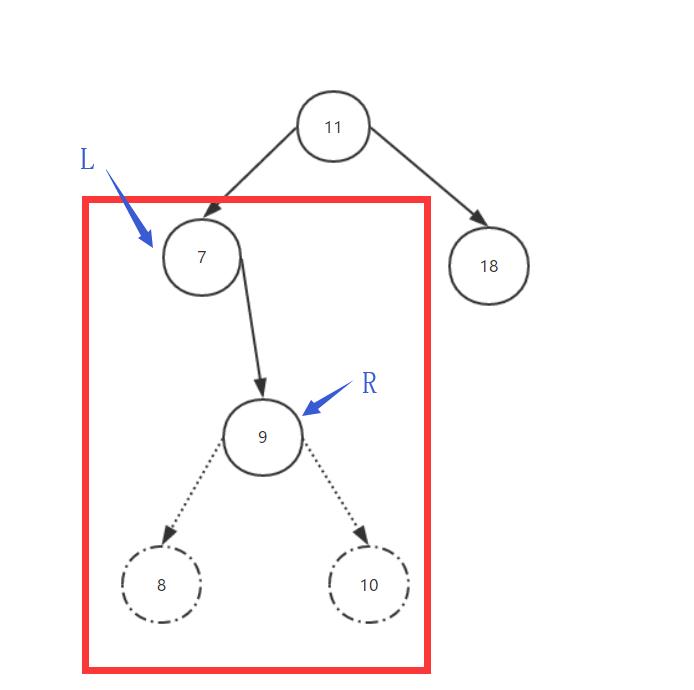
　　第三种情况：LR。

 

 

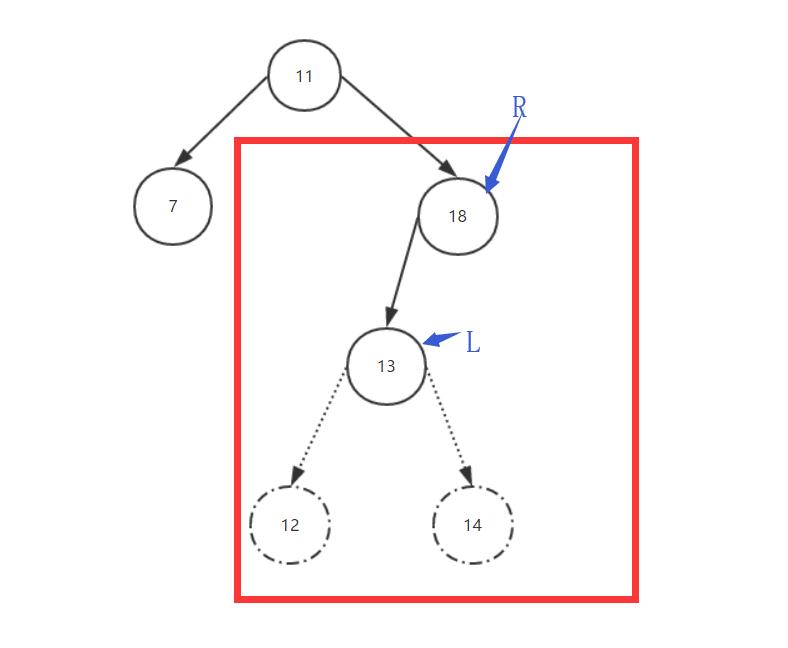
　　第四种情况：RL。

 

 　　那么看完上面这几幅图想必大家都了解了在插入节点的时候影响到树的*衡的4种可能性。那么为了面对这4种可能性。我们给出了与之相对应的4种解决不*衡的方法(其实就两种)。那么这里我们就要进入本篇最重要的内容了，旋转。在开始之前，希望大家记住一句话。那就是，什么情况导致的不*衡，那就用相反方向的旋转。什么意思呢，比如是LL导致的不*衡，那么我们就向右旋转。如果是RR导致的不*衡我们就向左，如果是RL，我们就LL再RR。如果是LR，我们就先RR再LL。好了，下面我们来看看究竟是如何旋转的吧。

　　　那么下面就有点意思了。希望大家可以仔细看。

一、RR情况的左旋转

　　我们还得来看图说话，我尽量把图画的让人容易误解，哦不，容易理解。

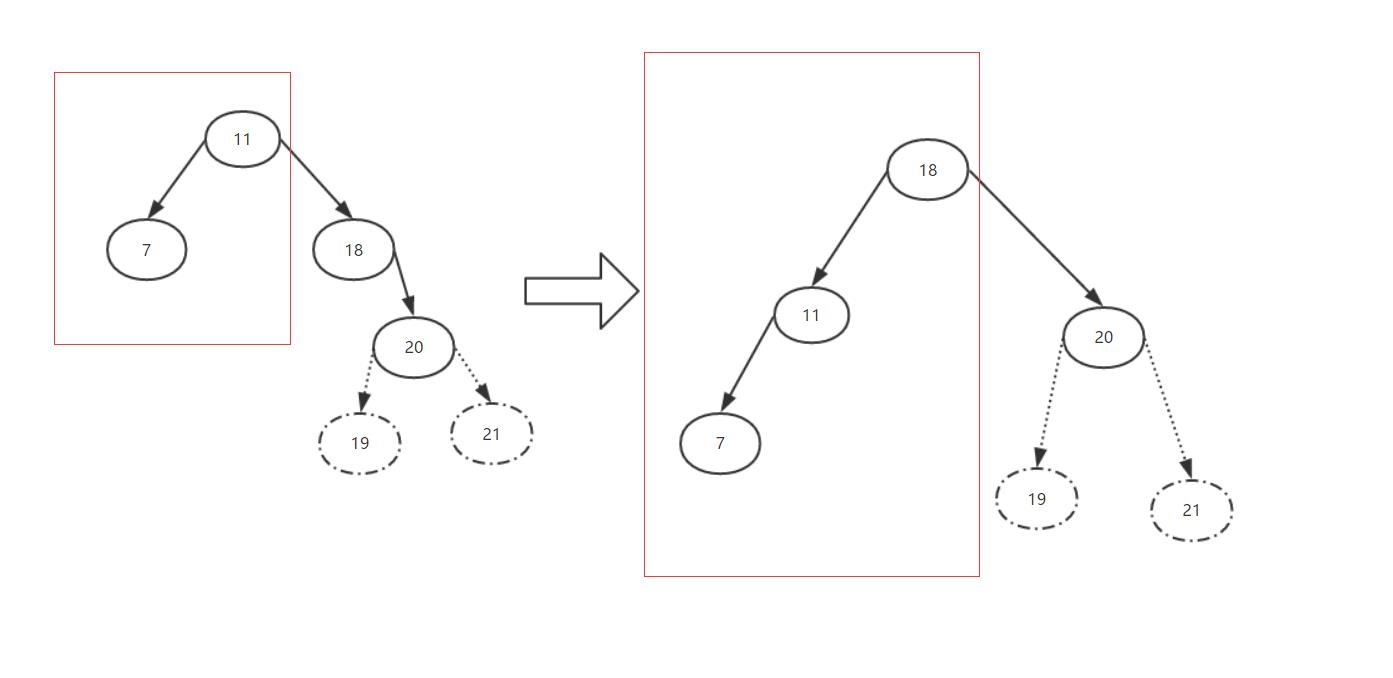
　　本人那个，画图工具用得还不是太熟练，拐歪的曲线没画出来，我拿嘴说吧......

　　大家看上图，左旋是以18为轴心整个树的左部分向左旋转，这样就使18变成了根节点，11变成了18的左侧子节点。这样旋转一下，就相当于减少了一层右侧字树的一层深度，从而使整颗树变成了*衡树。那么可能还有下面的这种情况，但其实是一样的。

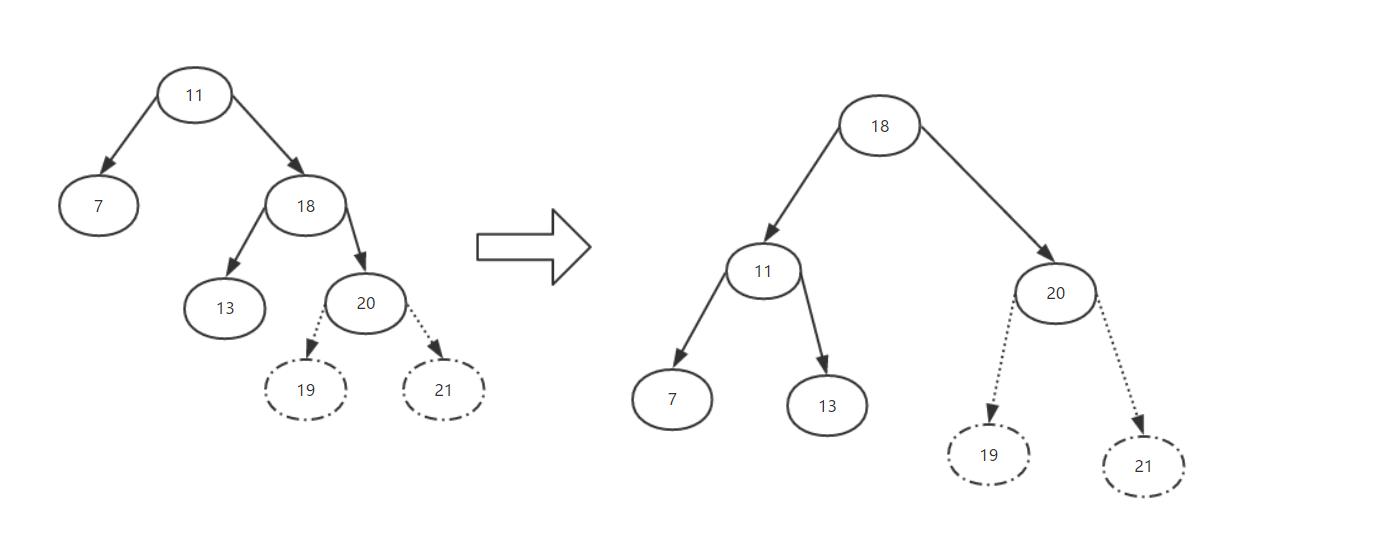
　　那么这种情况是要旋转的轴心节点（18），还有左侧子节点，在旋转之后，18的左侧子节点13就会变成11的右侧子节点。其实可以简单的认为是左旋过后被节点11给“挤”过来的。

　　其实，18的左侧子节点在旋转过后会成为11的右侧子节点还有一个原因，就是，18左侧子节点的值一定是大于11小于18的（旋转之前的图）。为什么自己想。那么在旋转过后，它也一定是大于11的，所以它可以成为11的右侧子节点。

一、LL情况的右旋转

 　那么LL情况的右旋转就没什么好说的了，跟RR情况是一样的，我们直接上图吧。

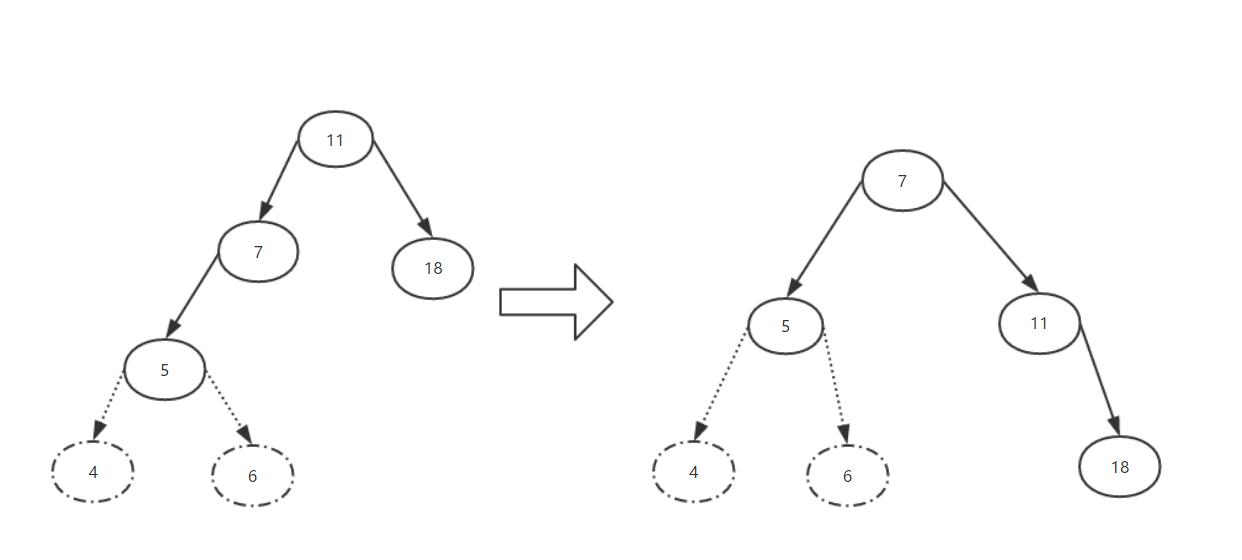
　　这绝壁没问题吧，原理都是一样的。只不过换了一个方向而已。

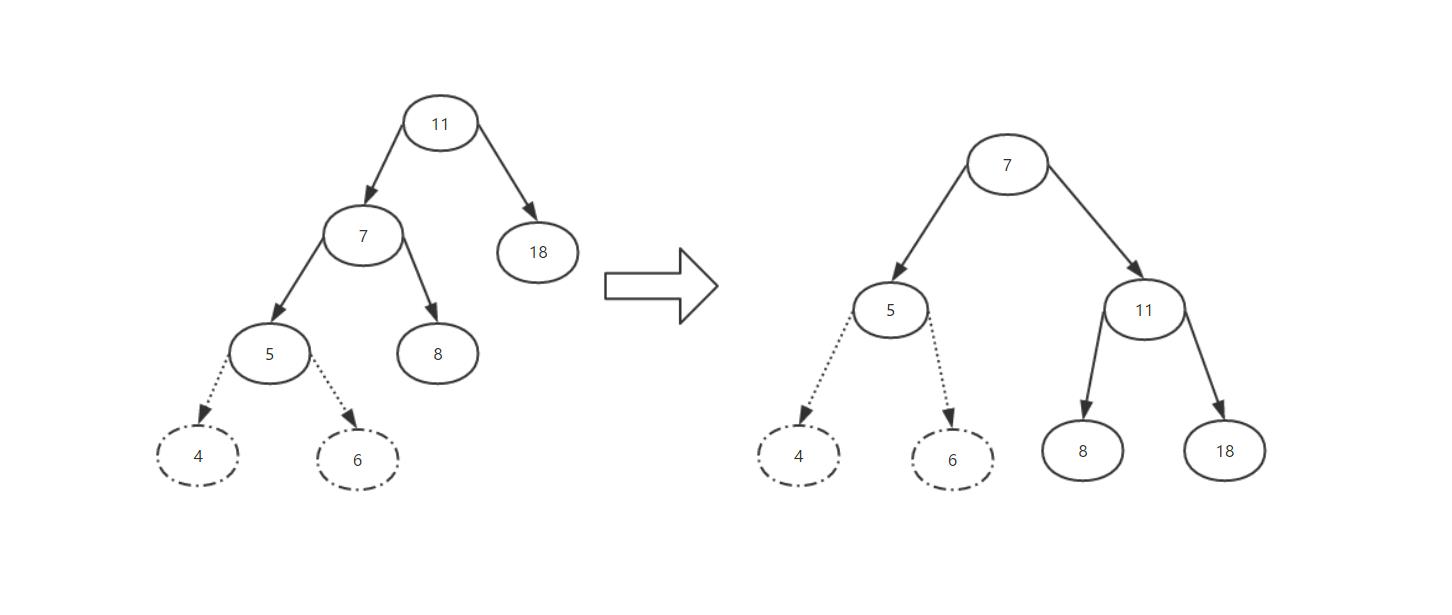
　　这样没啥好说的了，对吧。下面我们看看其他地情况。双旋转......

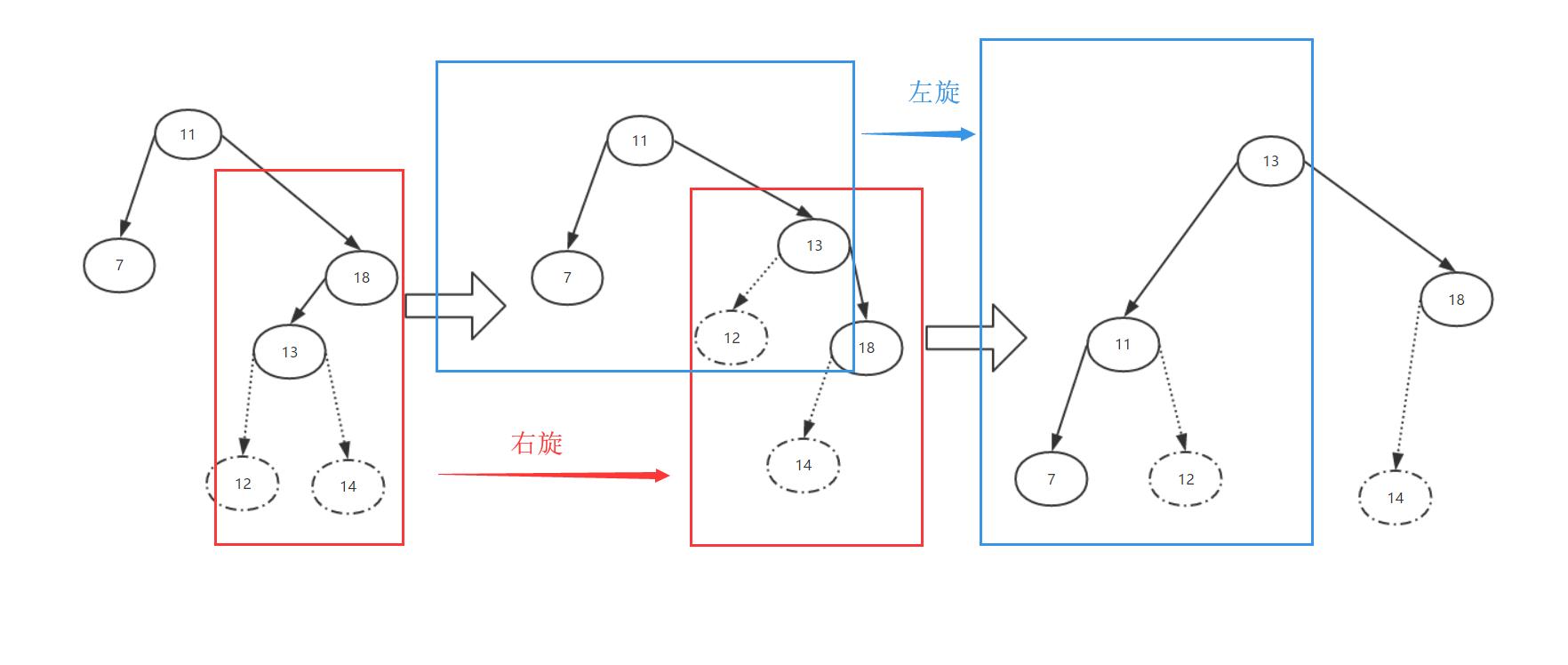
三、LR情况的左旋（RR）再右旋（LL）

　　我们还是直接上图，然后再解释，解释完这个RL情况的又不用再啰嗦了。挺好......挺省事，嘿嘿。

　　其实让人有点懵逼的是名字，我特意加了个括号，希望你别懵逼。

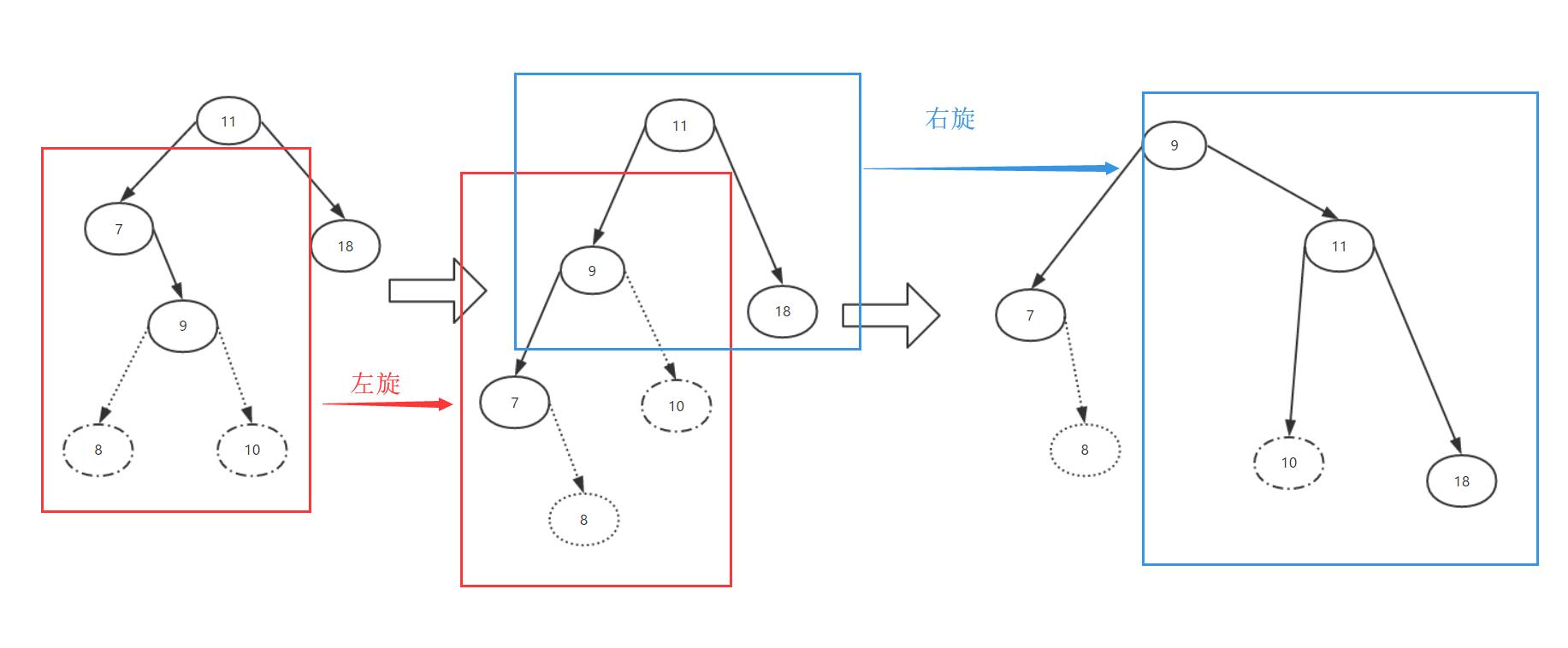
　　不知道大家看没看懂，总感觉这图不是很友好啊，还有8节点的小瑕疵就不要在意了，反正都是虚线......还有指向节点10的那条线是虚线.....不影响.....嘿嘿。

　　解释一下，我们需要双旋转的情况下，第一次旋转的是红框部分，也就是说，如果我们需要双旋转，两次旋转的轴心点是不一样的，第一次旋转的轴心是插入节点的父节点，而第二次旋转的轴心是插入节点的祖父节点。大家一定要注意。

　　那么这里可能会有一个疑问，就是8节点在第一次旋转过后，为什么会成为7节点的右侧子节点。这里十分重要，直接关系到你是否理解了AVL树的旋转。

　　我们先看第一次旋转，如果插入的是8节点而不是10节点，那么在第一次左旋的时候，节点7会成为节点9的左侧子节点，而这个时候8节点是无处可去的，因为7占了我的位置，这咋整，不能因为一次*衡就删除我这个节点啊，节点8肯定不干，不然你插入我干啥.....哎？感觉有点不对劲.....额咳咳....咱们继续吧....而节点8这个位置一定比9小比7大，所以我们在旋转过后，让它成为7节点的右子节点就可以了。希望我说明白了。

　　那么这个时候可能还存在7节点有左侧子节点的情况，上面没画，没关系啊，你是7节点的左侧子节点，左旋转过后你还在原来的位置，没人占你的位置，你就不用动了。嗯，就这样.....完毕！

四、RL情况的右旋（LL）再左旋（RR）

　　其实这里真没啥好说的了，我一点都不解释，大家自己看，看不懂你就从头看！

　　唉.......说了一大堆，终于可以到最后的代码了，上代码！

 

//这是我们计算当前节点的高度的方法
    var heightNode = function (node) {
        // 如果没有那就为-1
        if(node === null) {
            return -1;
        } else {
            // 如果存在执行逻辑
            //那么说一下这里我的理解吧，Math.max比较左节点和右节点的大小，返回大的那个值，然后 + 1。
            //为什么要返回大的那个值呢？因为如果左节点存在，那么值为0（-1 + 1）；并且右节点是不存在的，那么右节点为-1。
            //但是此时我们是有高度的，所以我们要选取有高度的那个节点，也就是值大的那一个。
            //那为什么要+1呢？因为高度只能为0不能为-1。-1是我们通过相减计算得到的，而不是计算高度得到的。记住这里是计算高度。
            console.log(Math.max(heightNode(node.left),heightNode(node.right)) + 1)
            return Math.max(heightNode(node.left),heightNode(node.right)) + 1;
        }
    }

    //RR:向左的单旋转
    var rotationRR = function (node) {
        var tmp = node.right;
        node.right = tmp.left;
        tmp.left = node;
        return tmp;
    }

    //LL:向右的单旋转
    var rotationLL = function (node) {
        var tmp = node.left;
        node.left = tmp.right;
        tmp.right = node;
        return tmp;
    }

    //LR:向右得到双旋转
    var rotationLR = function (node) {
        node.left = rotationRR(node.left);
        return rotationLL(node);
    }

    //RL:向左的双旋转
    var rotationRL = function (node) {
        node.right = rorarionLL(node.right);
        return rorarionRR(node);
    }

    var balanceInsertNode = function (node,element) {
        // 如果node的位置没有值，那么直接加入就好了。
        if(node === null) {
            node = newNode(element);
        // 如果假如的值是小于当前节点的话，说明我们要加在当前节点的左侧。
        } else if(element < node.key) {
            node.left = insertNode(node.left,element);
            // 那么下面就要判断是否是null，如果是null，那么没问题，直接加上就好了。
            if(node.left !== null) {
                // 如果不是，我们就要计算node的左侧高度减去右侧高度是否大于1，如果是，说明不*衡，需要来调用*衡方法来*衡。
                if((heightNode(node.left) - heightNode(node.right)) > 1) {
                    // 如果当前插入的节点的值小于node.left的值，说明是LL的情况，我们需要右旋。否则的话我们就需要先左旋，再右旋。
                    if(element < node.left.key) {
                        node = rorarionLL(node);
                    } else {
                        node = rorarionLR(node);
                    }
                }
            }
        } else if(element > node.key) {
            node.right = insertNode(node.right,element);

            if(node.right !== null) {
                if((heightNode(node.right) - heightNode(node.left)) > 1) {
                    if(element > node.right.key) {
                        node = rorarionRR(node);
                    } else {
                        node = rorarionRL(node);
                    }

                }
            }
        }
    }

 　　代码中多了一个balanceInsertNode方法，这个方法是需要替换我们前面写好的insertNode方法的，这样写是为了让大家更好的对比下。这些代码不像以前那样，写了一大堆的注释用来解释。其实要说的很多，都在前面的图和语言描述中说过了。所以大家看这个代码的时候。有不明白的地方，对照着前面的逻辑一点一点看，肯定就看明白了。比如rotationLL和rotationRR内部的替换以及为什么要这样替换，都在前面说过了。所以就不再在代码中啰嗦了。

　　这一篇文章有点长，也花了我一点心思才完成。很重要，如果你想要对树有一个不错的了解，这些必须要会。我尽可能的用我理解的思路给大家讲解，如果有什么不清楚的地方，大家可以留言讨论。

　　哦对了，本来还要跟大家说说其他树的，但是想了想也没什么必要，给大家一个链接，大家可以自行去做一些简单的了解，比如红黑树，堆积树，还有B树等等等等。种类很多。要想都讲完大概几十篇都不够，希望这两篇树结构的文章可以抛砖引玉。让大家提起对数据结构的兴趣。

　　大家可以看一下这个了解https://zh.wikipedia.org/wiki/AVL%E6%A0%91，滑动到页底，你就能看到其他的树结构了。

　　好了，终于，自*衡二叉搜索树到这里基本就结束了。下一部分会讲解最后一种也是最复杂的一种非线性数据结构——图。

 

　　最后，由于本人水*有限，能力与大神仍相差甚远，若有错误或不明之处，还望大家不吝赐教指正。非常感谢！