DQN蒙特卡洛树搜索（MCTS）

Posted 2023-02-16 Hellsegamosken

DQN

Q-learning

Q(s,a): 状态 s 下采取动作 a 的期望收益

$Q(s,a)\leftarrow (1-\alpha )Q(s,a)+\alpha [r+\gamma {\max }_{a^{\prime }}Q(s^{\prime },a^{\prime })]$

• Q-predict：估计值，当前查 Q-table 得到的。
• Q-target：现实值，计算得到的，中括号内的。相当于我们的目标。
• r：reward，当步奖励

DQN

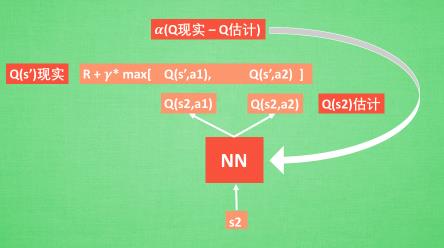
DQN = Q-learning + NN，用神经网络代替 Q-table，即 Q -value 是神经网络算出来的。再根据 Q-predict 和 Q-target 用神经网络的方式去更新参数，相当于更新 Q-table。

experience replay

简单来说， DQN 有一个记忆库用于学习之前的经历。 Q-learning 是一种 off-policy 离线学习法，它能学习当前经历着的， 也能学习过去经历过的， 甚至是学习别人的经历。 所以每次 DQN 更新的时候，我们都可以随机抽取一些之前的经历进行学习。随机抽取这种做法打乱了经历之间的相关性，可能利于神经网络的更新。

fixed Q-targets

DQL: Dueling Double DQN, Prioritized Experience Replay, and fixed Q-targets（三下）_mike112223的博客-CSDN博客_fixed q target

在 Bellman 方程中，每更新一次我们都会离目标更近，但目标也同步在变化，这就可能导致训练过程中的震荡。如果使用 fixed Q-targets，我们就会在 DQN 中使用到两个结构相同但参数不同的神经网络，预测 Q -predict 的神经网络具备最新的参数，而预测 Q -target 的神经网络使用的参数则是定期更新的（比如每 T 步）。这样在一段时间内，我们的目标是固定的。

on-line 与 off-line

1. 由于样本收集很困难，或者很危险。所以实时的和环境进行交互是不太可能的，那么可否有一种仅利用之前收集的数据来训练的方法去学习策略呢？
2. 不管它是on-policy还是off_policy，我只要经验回放池中的交互历史数据,去拟合函数是否可行？
3. 仅利用轨迹数据学习的策略能否和Online算法的媲美？

on-policy 与 off-policy

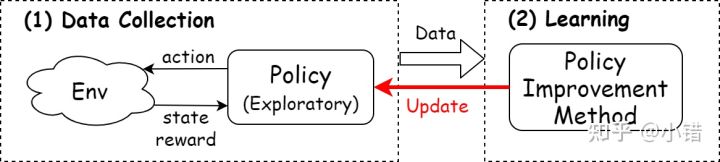
当前策略提供的动作不一定最优，所以必须要有随机搜索的能力（尝试非最优动作）。

off-policy：将收集数据当做一个单独的任务。它准备两个策略：行为策略(behavior policy)与目标策略(target policy)。行为策略是专门负责学习数据的获取，具有一定的随机性，总是有一定的概率选出潜在的最优动作。而目标策略借助行为策略收集到的样本以及策略提升方法提升自身性能，并最终成为最优策略。Off-policy是一种灵活的方式，如果能找到一个“聪明的”行为策略，总是能为算法提供最合适的样本，那么算法的效率将会得到提升。

而 on-policy 采用的是当前策略搜集的数据训练模型，每条数据仅使用一次。

the learning is from the data off the target policy.

也就是说RL算法中，数据来源于一个单独的用于探索的策略(不是最终要求的策略)。

以 Q-learning 为例，算法数据收集部分用的策略是 Q-table 构造的 epsilon-greedy 策略，而不是完全基于 Q-table 的目标策略，因此是典型的 off-policy。

Importance Sampling

蒙特卡洛积分中，如果在 $f(x)$ 对积分贡献大的区域进行相对密集的采样，可以在采样数不变的情况下增加准确度，减少方差。

换句话说，如果我们对 x 的采样本身就满足一个分布 $p(x)$，那么 $p(x)$ 和 $f(x)$ 越接近，统计量的方差就越小。

蒙特卡洛积分与重要性采样详解 - 烈日行者 - 博客园 (cnblogs.com)

go-explore

【伏羲讲堂】强化学习的探索方法简介 - 知乎 (zhihu.com)

主要解决 hard - exploration 的问题：

1. 奖励稀疏（sparse）。需要做出特定的一连串动作才能获得一个非零奖励。
2. 奖励有误导性（deceptive）。比如小动作有负奖励，会导致 agent 原地不动，停止探索。

最简单的方法是认为设计 reward 来引导 agent，但需要先验知识，并且可能会限制 agent 甚至将其带偏。

与之相对的，可以引入内在奖励（intrinsic reward）

Intrinsic Reward

Count-based exploration 中 intrinsic reward 来源于 agent 对所遇到的状态的“新奇”程度。算法直接统计 agent 到达某个状态的次数来衡量再次到达该状态带来的 intrinsic reward，次数越少 agent 获得的 intrinsic reward 越大。

在高维的状态空间中，agent很难重复访问到一个完全相同的状态，会导致统计到的访问次数非零的状态极少。为解决这个问题，一种方法是使用密度模型（density model）来近似估计一个状态被访问的频率，并依据访问频率推导一个状态的 pseudo-count；另一种方法是采用 Locality-Sensitive Hashing 将相近的状态映射到相同的 hash code。

Prediction-based Exploration 中 intrinsic reward 来源于 agent 对状态变化的“惊讶”程度。agent 通过学习一个 prediction model 预测环境变化，预测结果与实际结果之间的差值越大，说明 agent 对这部分环境的变化规律越不熟悉，对环境的探索获得的 intrinsic reward 就越高。

go-explore

采用 intrinsic explore 的方法，会产生 detachment 问题。想象 agent 一开始在一座桥的中央，如果它一开始往左走，获取了左半部分的 intrinsic reward，那么它就很难再探索到右边去了。

为解决 detachment 的问题， go-explore 方法分为两个步骤。

• explore until solved
  1. 从 archive 中随机抽取一个之前访问到的 state
  2. 按照记录的轨迹回到这个 state
  3. 从这个 state 出发继续探索 N 步
  4. 探索过程中如果在某个状态下获得了更高的分数（extrinsic reward），则将这个状态及路径记录在 archive 中
• 使用上一部分保存的轨迹进行 self-imitation learning

self-imitation learning

Go

Monte Carlo tree search（MCTS）

蒙特卡罗方法、蒙特卡洛树搜索（Monte Carlo Tree Search，MCTS）初探 - 郑瀚Andrew.Hann - 博客园 (cnblogs.com)

一种基于树结构的，在搜索空间巨大时仍有效的方法，结合了随机模拟的一般性和树搜索的准确性。

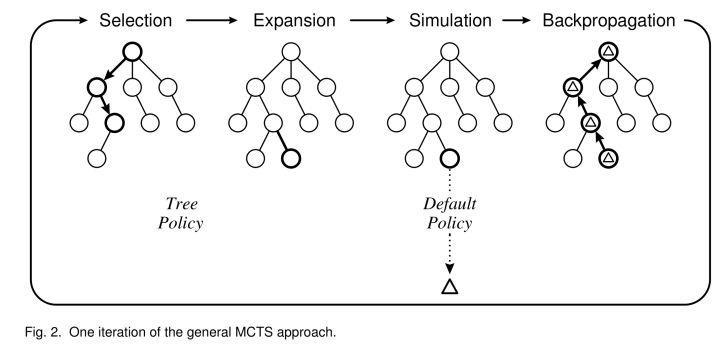
MCTS 的过程即是构造搜索树的过程，按照一种非对称的策略进行树的搜索空间拓扑结构增长。这个算法会更频繁地访问更加有可能导致成功的节点，并聚焦其搜索时间在更加相关的树的部分。每个节点维护访问次数以及累计评分。每次迭代分为四个步骤：

1. 选择（selection）。从根节点出发向下一路选择出一个最急迫需要被拓展的节点N。对于某个结点有三种情况：
   • 该节点所有可行动作都已经被拓展过：如果所有可行动作都已经被拓展过了，这表示该节点已经完成了一个完整搜索（complete search），那么我们将使用UCB公式计算该节点所有子节点的UCB值，并找到值最大的一个子节点继续检查。反复向下迭代。
   • 该节点有可行动作还未被拓展过：如果被检查的局面依然存在没有被拓展的子节点(例如说某节点有20个可行动作，但是在搜索树中才创建了19个子节点)，那么会在剩下的可行动作中随机选取一个动作（子节点）A，执行下一步的拓展（expansion）操作。
   • 该节点游戏已经结束了(例如已经连成五子的五子棋局面)：如果被检查到的节点是一个游戏已经结束的节点。那么从该节点直接执行反向传播（backpropagation）步骤。
2. 拓展（expansion）。新建一个节点，表示步骤 1 中拓展出的节点。
3. 模拟（simulation）。给新建节点一个初始评分。可以从该局面开始以既定策略或者随机策略完成一局游戏。
4. 反向传播（backpropagation）。更新选中节点到根路径上每个结点的累计评分。

每一次迭代都会拓展搜索树，随着迭代次数的增加，搜索树的规模也不断增加。当到了一定的迭代次数或者时间之后结束，选择根节点下最好的子节点作为本次决策的结果。

https://zhuanlan.zhihu.com/p/32335683)

Upper Confidence Bounds（UCB）

Multi-Armed Bandit: UCB (Upper Bound Confidence) - 知乎 (zhihu.com)

epsilon-greedy 生硬的将选择过程分为探索阶段（exploration）和利用阶段（exploitation），在探索阶段对所有物品以相同的概率进行探索，不会用到历史信息，包括（1）某道菜被探索的次数，（2）某道菜获得好吃反馈的比例。

因此，我们采用 UCB 的方式
$$v_i+C\times \sqrt{\frac{\ln N}{n_i}}$$
vi 是结点估计值，ni 是访问次数，N 是其父节点访问次数，C 是超参数。

UCB 公式对已知收益节点加强收敛，同时鼓励接触那些相对未曾访问的节点的尝试性探索。这是一个动态均衡公式。

最强通用棋类AI，AlphaZero强化学习算法解读 - 译站 - AI研习社 (yanxishe.com)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OLadhR6F-1660187200431)(C:\\Users\\Hellsegamosken\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220625115007788.png)]

• 监督学习的策略网络 $p_{\sigma }$ ，根据棋盘状态输出概率分布。根据人类棋手的围棋历史数据预测落子，最大化在某个下与人类玩家动作的相似度，得到一个初步的策略网络。
• 强化学习，自我博弈，优化的策略网络 $p_{\rho }$，使其尽量赢得比赛。网络结构与上面一致。训练方法是随机选取之前的某个版本网络进行对弈，奖励赢一次+1，输一次-1。
• 训练一个可以预测胜率的网络 $v_{\theta }$ ，后面在MCTS中有用。

$p_{\pi }$ 是一个规模较小的网络，可以做快速预测。

之后，使用策略网络和值网络进行搜索