求总体为指数分布的矩估计和极大似然估计
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了求总体为指数分布的矩估计和极大似然估计相关的知识,希望对你有一定的参考价值。
解答:

设X~EXP(入)
E(X)=1/入
^入=1/(xbar)
L(入|x)=π(连乘符号)(i=1~n) 入e^(-入xi)
两边取对数 ,并使ln(L)=l
l(入|x)=ln(入^n)+(-入)Σ(xi)
求导
l'(入|x)=n/入-n(xbar)
让导数=0
0=1/^入-(xbar)
1/^入=xbar
^入=1/(xbar)
再检验l二阶导为负数,所以l有最大值,最大拟然估计为1/(xbar),同矩形估计。
定义
最大似然估计,只是一种概率论在统计学的应用,它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值。
最大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆就把这个参数作为估计的真实值。
参考技术A简单计算一下即可,答案如图所示
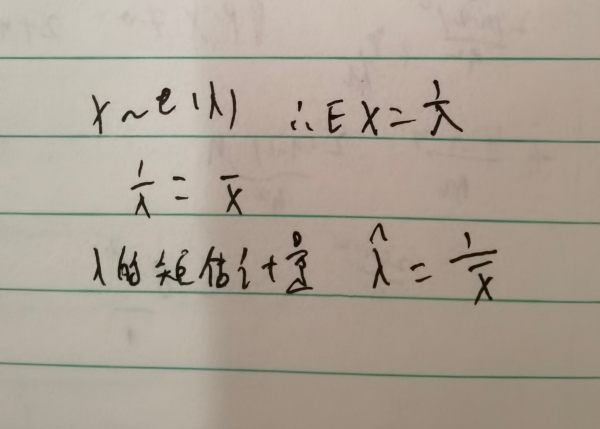


以上是关于求总体为指数分布的矩估计和极大似然估计的主要内容,如果未能解决你的问题,请参考以下文章