时域频域时频域+三种频域变换的理解

Posted 2023-03-15 五角场研究僧

0.引言

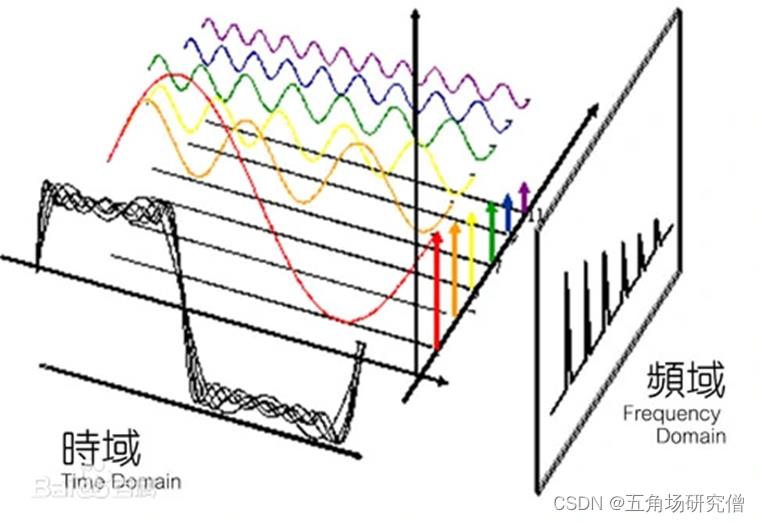
时域上的复杂，在频域上也许很规律，即使复杂如交响乐，也是1~7不同调子（蝌蚪文）的组合，并且有规律，即曲谱。
大统一的弦理论，似乎也是从频域去尝试解释世界，解释基本粒子。

对于理工科，频域变换，最大的作用就是把时域上复杂的微分方程转为频域上多项式，极大地方便离散求解。

基础资料：《信号与系统》和《复变函数》

1.时域和频域

时域：真实世界，唯一存在的域，我们的经历都是在时域中发展和验证；比如听音乐会，随着时间流逝，我们完整的欣赏这段音乐；这是时域中发生的事情，而频域，这段音乐只是由特地的音符组成的乐谱而已，这是永恒的与时间无关系。
**信号在：**时域转换频域。通过傅里叶变化；
时域来看，多个波形分析；
而频率可能具体某个值。
信号有噪声、有极限漂移；

直接线上通常时域，时间振荡情况；
然后还要频域，具体某个hz（频域，谱图）50hz；
时频：横轴时间，纵轴频率；
设定采样率；2000HZ
起始时间：一段零，另一个就要时间；
有大量50hz谐波成分。简单的带阻滤波器，49.5-50.5，滤出 50 hz成分；
滤掉话，即频域分析峰值没有了；时频图上也没有明显的。

时频分析:横轴时间，纵轴频率，颜色深浅表示情况。

3.常见的——三种频域变换的理解

傅里叶变换，操作真实的时域信号（确知信号）
简单的周期信号，使用傅里叶级数变换，得到离散的频率谱（离散的频率谱均是信号频率的整数倍）；非周期信号，使用傅里叶变换，得到连续的频率谱（非周期信号，近似可看作由无数种周期信号叠加形成，每一个变换后都形成对应的整数倍离散频率谱，无数种不同离散频率谱叠加，就是频域上的连续谱）。

拉普拉斯变换， 操作不收敛信号
主要用来计算微分方程

Z变换，相当于是离散的拉普拉斯变换
主要用来计算差分方程