机器学习------- 线性回归（Linear regression ）

Posted 2023-02-15 菜菜粥

发现网上有很多的原理讲解，其实这个大家都差不多会的，很少有提供代码参考的，我这里python直接实现出来，后面还会实现神经网络，回归树和其他类型的机器学习算法
先来一篇小试牛刀，个人表达能力不是很好，大家见谅

简要说下自己的理解：

训练一个Linear Regression，给定一组特征值（[x1,x2,x3,x4,...,xn]) 和 对应的结果 y，目标就是得到一个模型W权重向量

            图一                    图一表示原始训练数据集（当然训练规模 远比这个大，这里只是图形化理解下） 把图一扩充一列全为1，然后用训练出来的权重w（怎么训练下面会说到）和矩阵相乘可以预测结果，这里是用原数据集和训练出来的w来为以后计算模型的代价，当然给定一组新的数据，你就能用w来预测结果了。
图二用权重计算y值
图三原数据的y值




上图表达的是通用形式
在这个例子中，我们的预测模型就是Hypothesis，未正则化的代价函数J，后面是使用正则化来消除过拟合（什么叫过拟合，举个例子，简单的说就是，在训练集上的表现太好了可以看成100%正确预测训练集，就是你训练的模型，在原数据集上进行，预测结果是100%正确。那么就存在一个问题，本来一些干扰值本身就是干扰项，而你的模型却不能排除，那么在以后的数据集上你就会预测错误。换句话说，你不能很好容错率。我们希望有好的推广能力，而不拘泥于仅仅的训练集）
注意是要同时更新theta所有值 上图中J不能预防过拟合，所以用下图中的公式
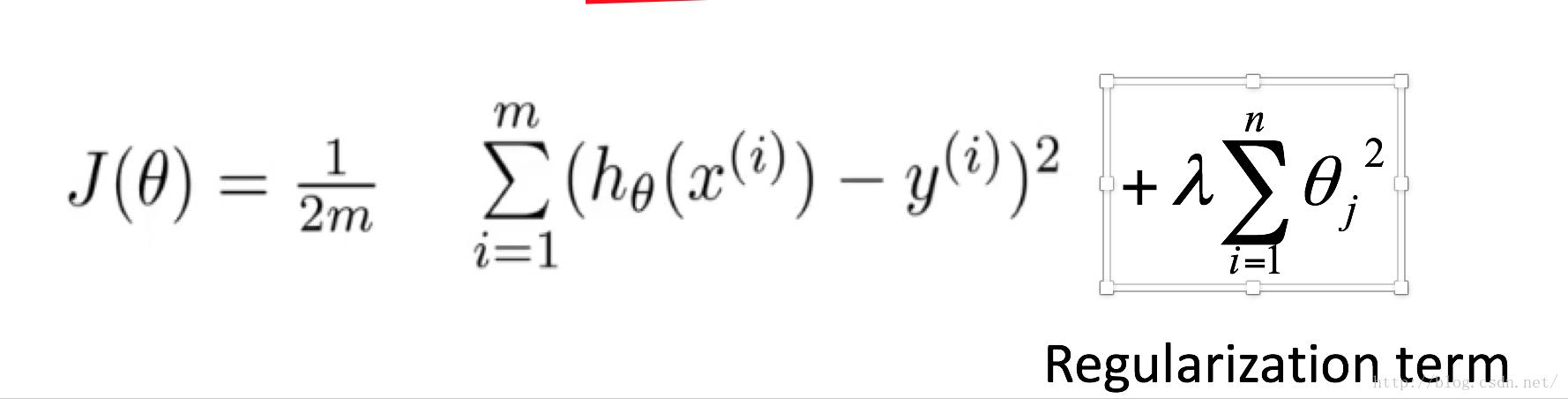
我们的目标是要是的J尽量等于0，相当于保证不过你和的情况下，让在数据集犯的错误尽可能的少。 注意观察预测函数的表达形式，theta0的系数为0，为了J的求导的统一形式，所以为X数据集填上一列1 所以上图为我实现的形式，代码为J就是代价函数，注意正则化theta是不包括theta0的（具体理解我是用极限法理解的，如果lambda很大，那么所有的theta都很小，留下theta0才能保证 正确，可以这样理解，theta0定义了一个基本调子，类似一个平均水平的意思，然后其他theta进行微调）

<pre name="code" class="python">def countCostFunc(X, y, theta, lamb):
    #X为训练集，y表示训练集上的lable，theta表示权重，lamb是正则常数
    #注意这里的X，theta都经过了扩充，X增加了一列1，theta增加了theta0，这主要是为了向量的统一运算
    m, n = np.shape(X)  #X矩阵行m，列n
    h = np.dot(X,  theta) #举证相乘
    regtheta = np.copy(theta)#深拷贝，因为，python是引用，
    regtheta[0,0] = 0
    J = ((np.dot((h-y).transpose(), (h - y))  +  lamb * np.dot(regtheta.transpose(), regtheta) )/ float(2 * m))
    grad = (1  / float(m)) * (np.dot(X.transpose(),  h-y) +  lamb * regtheta)  #对所有theta求导，这个就是J函数对theta分别求导后，然后变成一个列向量
    return J, grad

#theta多了theta0但是X还没有增加1列，用训练出来的模型，预测结果
def predict(X, theta):
    X = np.array(X)
    m,n = np.shape(X)
    X = np.hstack([np.ones((m, 1)), X]) #为X增加一列1
    h = np.dot(X, theta)
    return h

下面python代码为例子,实现一个完整的Linear Regression，原理通过代码阐述，注意下文中的theta也就是前面说到的w权重 生成简易的数据集，考虑好像简单形象化，并没有使用80M的数据集，而是临时生成简易的数据集。代码如下 一些导入的文件和库，具体说明看后面，python2.7

#coding=utf-8
import numpy as np
import grandDescent
import costFunction
import loadData
import predict
import write2File
import rmse
import os
import random
import matplotlib.pyplot as plt
from pylab import plot,show
from scipy import stats

生成数据集 横轴为X，纵坐标为y

def handle_data_self():
    X_train = np.array([0,1,2,3,4,5,6,7,8,9]).reshape(10, 1)
    y_train = np.array([0,2,3,4,5,6,7,4,9,10]).reshape(10, 1)
    X_cross = np.copy(X_train)
    y_cross = np.copy(y_train)
    X_test = np.array([0,1,2,3,4,5,6,7,8,9, 10,11,23,1]).reshape(14,1)
    plt.scatter(X_train, y_train, color="Red")
    # plt.show()
    return X_train,y_train,X_cross,y_cross,X_test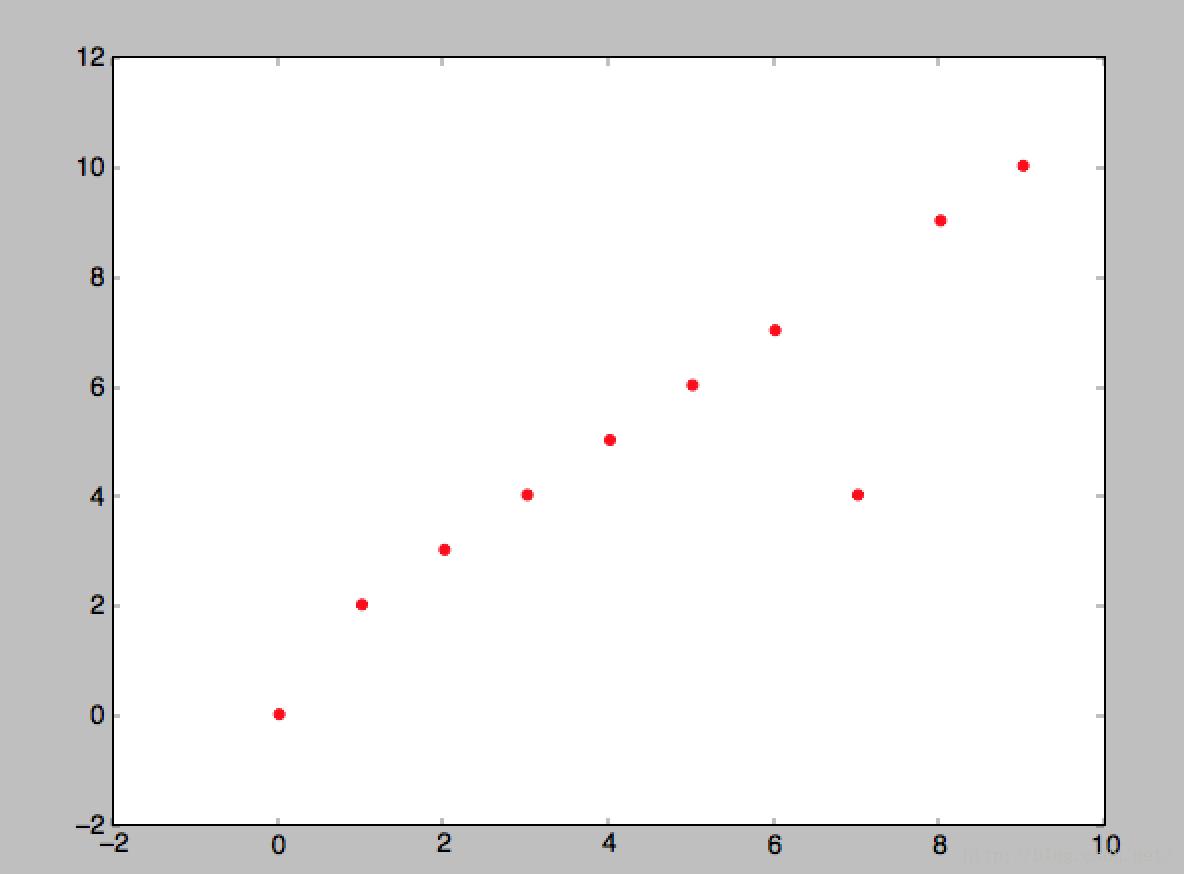

最后贴出主程序如下main.py

<pre name="code" class="python">#coding=utf-8
import numpy as np  #系统库
import grandDescent
import costFunction
import loadData
import predict
import write2File
import rmse
import os  #库 
import random #库
import matplotlib.pyplot as plt #库



def regression_simple(X, y, X1, y1, option):
    alpha = float(option["alpha"])
    maxCycles = int(option["maxCycle"])
    lamb = float(option["lamb"])
    save = bool(option["saveRecord"])
    add = bool(option["add"])
    optGoal = option["optGoal"]
    methods = option["method"]
    thetaPath = option["thetaWritePath"] if option.has_key("thetaWritePath") else None
    m,n = np.shape(X)
    J_train = None
    theta = None
    if methods == "stocGradDescent":
        J_train, theta = grandDescent.stocGradDescent(np.copy(X), y, maxCycles, alpha, lamb)
    elif methods == "grandDescent":
        J_train, theta = grandDescent.grandDescent(np.copy(X),  y, maxCycles, alpha, lamb)
    J_cross = costFunction.countCostFunc(np.hstack([np.ones((X1.shape[0], 1)), X1]), y1, theta, lamb)
    rmseResult = rmse.countrmse(np.copy(X1),y1,theta) #后面都是保存一些东西
    if save and thetaPath:
        if not add and os.path.exists(thetaPath):
            os.remove(thetaPath)
        file_object = None
        if not add:
            file_object = open(thetaPath, 'w')
        elif os.path.exists(thetaPath):
            file_object = open(thetaPath, 'a')
        else:
            file_object = open(thetaPath, 'w')
        file_object.write("J_traincost=>"+ str(J_train) + ",J_crosscost=>" + str(J_cross[0]) +  ",alpha=>" + str(alpha) + ",lamb=>" +  str(lamb) + ", Cycles=>"+ str(maxCycles) + ", rmse=>" + str(rmseResult) + "\\n" + ",theata==>"+str(theta.transpose()) + "\\n")
        file_object.close()
    J = None
    if optGoal == "J_train":
        J = J_train
    elif optGoal == "J_cross":
        J = J_cross
    elif optGoal == "rmse":
        J = rmseResult
    else:
        print "optGoal fault!!!"
    return J, theta



def handle_data_self():
    X_train = np.array([0,1,2,3,4,5,6,7,8,9]).reshape(10, 1)
    y_train = np.array([0,2,3,4,5,6,7,4,9,10]).reshape(10, 1)
    X_cross = np.copy(X_train)
    y_cross = np.copy(y_train)
    X_test = np.array([0,1,2,3,4,5,6,7,8,9, 10,11,23,1]).reshape(14,1)
    plt.scatter(X_train, y_train, color="Red")
    plt.show()
    return X_train,y_train,X_cross,y_cross,X_test

if __name__ == "__main__":
    print "load data..."
    X_train, y_train, X_cross, y_cross, X_test = handle_data_self()
    print "load data finished"
    print "进入traing..."
    action = "regression_grandDescent"
    J = None
    theta = None
    if action == "regression_grandDescent":
        option = "maxCycle": 400, "alpha": 0.05, "lamb": 0.001, "saveRecord": 1,
                  "thetaWritePath": "./thetaSave.txt", "add":1, "optGoal":"J_train",
                  "method": "grandDescent"
        J, theta = regression_simple(X_train.copy(), y_train.copy(), X_cross.copy(), y_cross.copy(), option)
        plt.plot(X_train, predict.predict(X_train, theta), color="Green")
        plt.show()
   
    print "完成traing"

    if action == "regression_grandDescent" or action == "regression_grandDescentWithBestAlphaAndLamb" or action == "regression_stocGradDescent":
        y_pre = predict.predict(X_test, theta)
        write2File.savePrediction(y_pre, path="sample_submission.csv")
    print "预测完毕","保存结果至sample_submission.csv"

其中

X_train, y_train, X_cross, y_cross, X_test = handle_data_self()
这里分别是，原始数据集X，原始数据集y，交叉验证集X，交叉验证y，检测集X

原始数据集X：就是给你的训练样本的特征值，注意这里还没添加X0为一，后面会在其他地方加上，为什么要加一列，是为了统一后面的导数计算，

grandDescent.py文件
<pre name="code" class="python">#coding=utf-8

import numpy as np
import operator
import copy
import math
import costFunction


def grandDescent(X, y, maxCycles, alpha, lamb):
    m,n = np.shape(X)
    theta = np.zeros((n + 1, 1))
    X = np.hstack([np.ones((m,1)), X])
    J = 0
    for i in range(maxCycles):
        J, grad = costFunction.countCostFunc(np.copy(X), y, np.copy(theta), lamb)
        #print "J的第",i+1,"次==>" ,J
        theta = theta - alpha * grad
    return J, theta

costFunction.py文件
<pre name="code" class="python">#coding=utf-8

import numpy as np
import operator
import copy
import math





def countCostFunc(X, y, theta, lamb):
    m, n = np.shape(X)
    h = np.dot(X,  theta)
    regtheta = np.copy(theta)
    regtheta[0,0] = 0
    J = ((np.dot((h-y).transpose(), (h - y))  +  lamb * np.dot(regtheta.transpose(), regtheta) )/ float(2 * m))
    grad = (1  / float(m)) * (np.dot(X.transpose(),  h-y) +  lamb * regtheta)
    return J, grad

rmse.py 文件
#coding=utf-8

import numpy as np
import operator
import copy
import math
import costFunction


def countrmse(X, y, theta):
    m,n = np.shape(X)
    theta = theta
    #扩展1
    X = np.hstack([np.ones((m,1)), X])
    h = np.dot(X , theta)
    #按列求和
    sumDiffY = np.dot((h - y).transpose(), (h - y))
    J = sumDiffY / float(m)
    #print np.shape(J)
    return math.sqrt(J)


predict.py文件

#coding=utf-8
import numpy as np
import costFunction


#theta多了theta0但是X还没有增加1列
def predict(X, theta):
    X = np.array(X)
    m,n = np.shape(X)
    X = np.hstack([np.ones((m, 1)), X])
    h = np.dot(X, theta)
    return h

write2File.py文件
def savePrediction(y_pre, path):
    file_object = open(path, 'w')
    file_object.write("Id,reference\\n")
    for i in range(len(y_pre)):
        file_object.write(str(i) + "," + str(y_pre[i][0]) + "\\n")

最红结果如下：红点表示预测原来的数据集，绿色的线表示用训练出来的额theta计算的结果



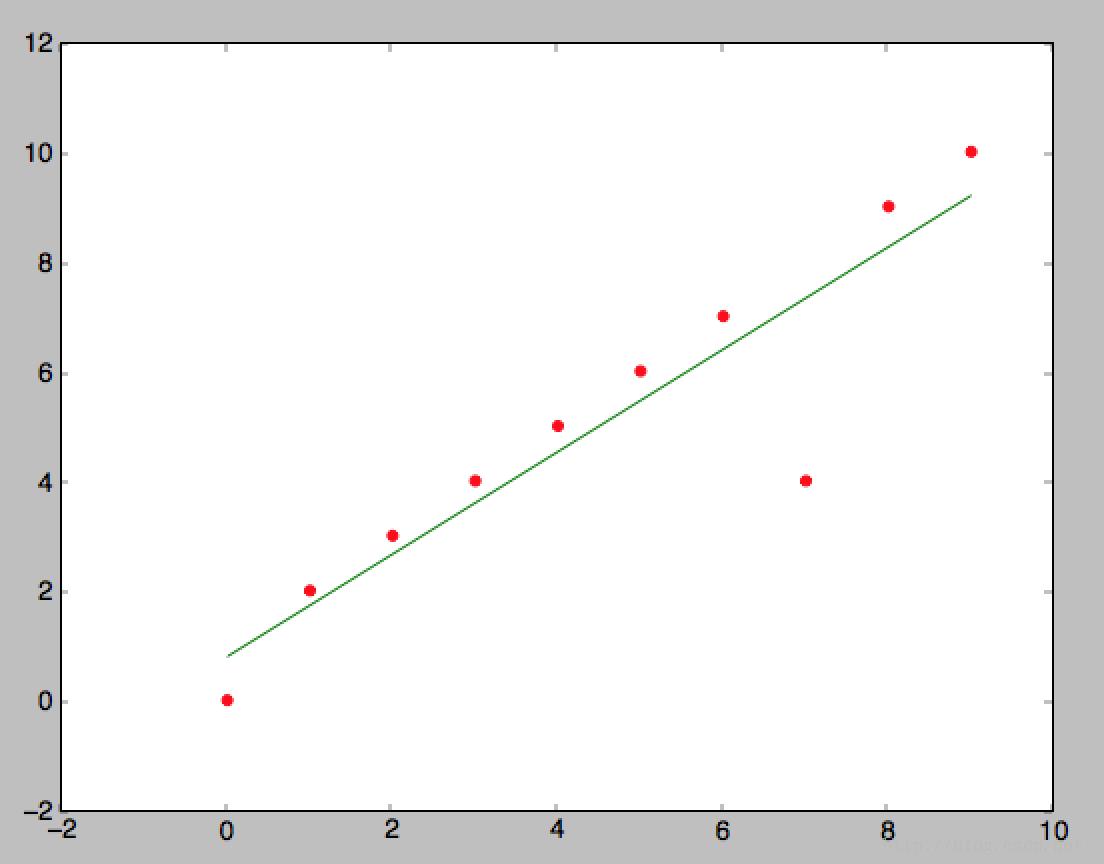
本文主要是用python，采用梯度下降的方法实现了正则化的Linear Regression 总结一些重要的地方， 1我这里没进行数据的预处理，因为各个特征值得数量级要保持一样。有两种方法， 第一种一般会采用把所有的数据集的变为均值为0，方差为1（x= (x - 这一列均值)/这一列标准差 ） 第二种变为-0.5到+0.5之间（x=(x-min)/(max-min) 对每列求得最小值和最大值，然后对每个值这样处理）， 

2.增加数据集一列1，theta增加theta0，是为了能统一计算梯度，而不用对theta0特殊计算
3.除了梯度下降（小规模数据） 还有随机梯度下降（适合大规模数据，比如上G的量，未演示出来，如果需要，后面会给出） 采用线性代数直接求X*theat = y的方法( 这种方法有特定条件限制，一般不采用），下图解决不可逆问题，但是由于矩阵求逆在矩阵很大的时候，计算误差很大，所以一般不采用


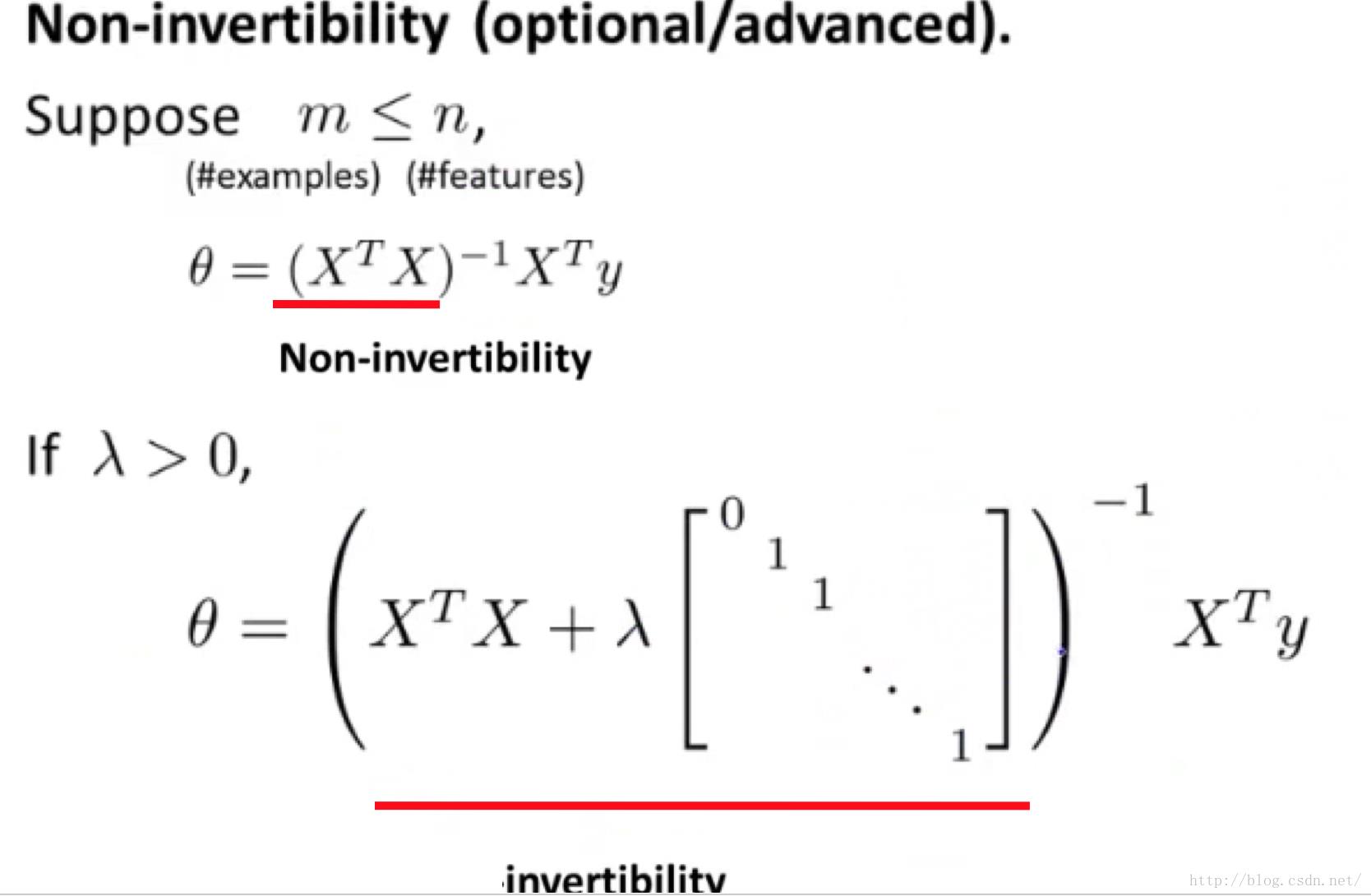
4正则化是使用的L2平方，这样好计算导数， 还有更好的L1，采用绝对值，效果更好 但是不好计算导数，所以这里没涉及 5这里只是两个theta0和theta1， 略微大一点都有上万的，预测值都是采用线性加权的方法
6另外关键的是，alpha和lambda的设定，都是经验值，alpha 一般你可是尝试一下组合

alphas = [0.1, 0.05, 0.01, 0.005, 0.001, 0.0005, 0.0001]
maxCycles = 200
lambs = [100,10,1,0.1,0.01, 0.001]

7并行化处理还没涉及，因为工业化必要分布式的，在有限的时间中训练出来，线性模型简单，预测速度快，仍然是一个主流算法