微积分溯源：当我们谈基本定理时，我们在谈什么？

Posted 2023-03-09 turingbooks

所谓微积分溯源，自然要回到历史语境中——定积分的概念来源于处理实际问题，而如今大学生学习的积分与微分是互为逆运算，是经历了许多伟大数学家思考论证得出的精粹。不了解历史脉络并不影响我们使用微积分，但这样去学习可能会把凝练的伟大思想当成既定的事实。

撰文 | 陈见柯

在一篇 2011 年发表于 《美国数学月刊》（American Mathematical Monthly）的文章里，作者开篇列出了名为 fundamental theorem of integral calculus (以下简称FTIC) 的定理：

[FTIC]对于区间[a, b]上的任意连续函数f，有

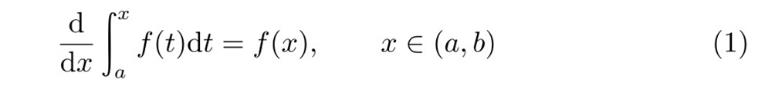
并且，如果对于所有的x∈(a, b)，有F'(x)=f(x)，则

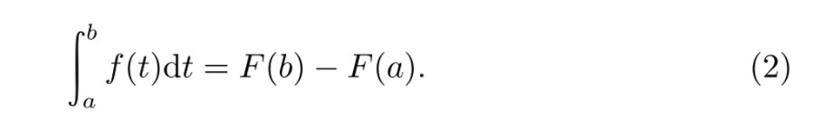
我们提两个问题：

(i) FTIC 应该如何翻译?

(ii) 微积分 (学) 基本定理是什么?

calculus的本义是小卵石，这个含义被保留在医学术语里，翻译为结石。在calculus成为以微分、积分为主题的一门课程之前，它在数学中的意思是计算方法。除去differential calculus、integral calculus这样与微积分密切相关的术语外，还有algebraical calculus、exponential calculus和symbolic calculus等术语。这样看来，将FTIC翻译成积分学基本定理应是准确的。在发表于《数学译林》的译稿中，陆柱家老师就是这么做的。在本书的中译本里，我们也是这么做的。第一个问题似乎过于简单了。然而，为了做到这步，我们还是走了一些弯路。

根据定理的表述，将公式(2)称作微积分基本公式，或者牛顿–莱布尼茨公式，是比较通用的做法。我们可以在同济大学数学系主编、面向非数学专业的微积分教材《高等数学》，华东师范大学数学系编写、面向数学专业的教材《数学分析》，以及小平邦彦的《微积分入门》中看到这样的表述。包括笔者在内的许多人都会想当然地认为公式(2)就是微积分(学)基本定理，这的确是上文提及的《高等数学》的表述。20世纪80年代（其实开始的时间要更早），科学出版社曾组织国内数学专业的专家学者们翻译了日本数学会编写的《数学百科词典》；其中“微分和积分的关系”这个词条也是将公式(2)称作微积分基本定理^[注释1]。若考虑新近的教材或者讲义，高等教育出版社的《简明数学分析》，清华大学数学系、丘成桐数学科学中心的于品教授为丘成桐数学英才班开设课程所编写的《数学分析之课程讲义》(定理128)，也都采用了这种表述。换言之，微积分（学）基本定理就是牛顿–莱布尼茨公式。

然而真是这样吗？公式(1)的部分如何理解呢？将 FTIC 中的integral删掉，直接写成 fundamental theorem of calculus（以下简称 FTC），岂不是更简洁？彼得·拉克斯与玛利亚·特雷尔的《微积分及其应用》（Calculus with Applications and Computing）、詹姆斯·斯图尔特（James Stewart）的《微积分》（Calculus: Early Transcendentals）以及斯蒂芬·阿博特（Stephen Abbott）的《分析入门》（Understanding Analysis）都是采用了FTC的表述^[注释2]，并且将公式 (1)和(2)分别称作定理的第一部分和第二部分。看一看国内比较有代表性的情况：郇中丹教授是前文提及的《简明数学分析》的作者之一。他在面向北京师范大学数学专业的大一新生讲授《数学分析》的视频公开课中，明确提到：“微积分基本定理就是讨论积分上限函数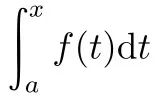 的性质”。再翻一翻中文教科书。华东师范大学数学系编写的《数学分析》明确地将公式(1)称作微积分学基本定理，并给出如下说明：

本定理^[注释3]沟通了导数和定积分这两个从表面上看去似不相干的概念之间的内在联系，同时也证明了“连续函数必有原函数”这一基本结论, 并以积分形式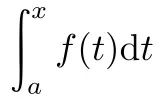给出f的一个原函数。

这无疑是一个精准、凝练的叙述。打一个不算恰当的比喻，公式(1)与公式(2)的关系像是“道”与“术”的关系一样：公式(1)回答了“有还是无”的问题，公式(2)回答了“怎么算”的问题。将公式(1)和公式(2)综合地写成一个定理，才是更完整的叙述。值得一提的是，东南大学丘成桐中心、东南大学数学学院的李逸教授新近编写的《基本分析讲义》里，也是写成了微积分基本定理第一部分和第二部分的形式。在中文微积分或者数学分析主题的教材、讲义以及译著里，这是我们唯一看到明确将公式(1)与公式(2)合写成一个定理的叙述^[注释4]；但若把搜索的范围再扩大一点儿，在实变函数主题的中文教材中，倒是可以看到合写的表述。

为了回答最初提及的两个问题，我们还要再多走一点点。与华东师范大学版《数学分析》配套的参考资料《数学分析(第四版)学习指导书》的“定积分”一章里，指明了如下说法同样值得我们注意：

从数学发展历史看，形成定积分概念远早于不定积分的概念。

确实如此。正如本书第一章的标题是累积（accumulation），谈到定积分，大部分教科书会从计算图形面积、物体体积、位移等具体问题展开。尽管用无限分割、近似求和、求极限的方法定义定积分直到柯西的时代（19 世纪）才宣告完成，但问题本身伴随着测量的出现就已经出现。许多教材会将定积分的内容安排在不定积分之后。从教学的角度而言，这种做法的确带来了很多便利；但这并不是历史发展的先后顺序。尽管“微分与积分是互逆的运算”非常凝练，但这是先贤们不断探索之后的高度总结。更麻烦的问题在于，如果我们理解得不够好，单纯地将积分理解为—–或者干脆定义为—–微分的逆（一个显然的事实是，并不是所有教微积分、数学分析的从业者都能达到郇中丹老师的高度），这就会使得原本处于微积分核心地位的公式(1)变成了近乎平凡的事实。出于以上的诸多考量，在考证了术语的演化之后（详见第2.7节的脚注2)，作者不厌其烦地、坚决地使用术语FTIC，而非FTC。尽管定积分是通过求和、求极限的方式定义的，深刻的是，这样定义的定积分可以用微分的逆进行求解和计算， 而FTIC的第一部分就是沟通微分和积分的桥梁。从计算的角度，如果要考虑定积分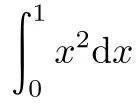，比起将区间[0, 1]进行n等分，然后在第i (i ≥ 1)个小区间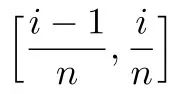选取小区间的右端点的函数取值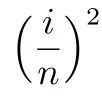，近似得到曲边梯形的面积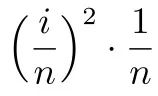，进而求和、求极限的做法

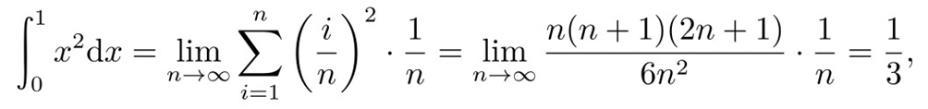
我们更习惯的直接借助微积分基本公式（即FTIC的第二部分），

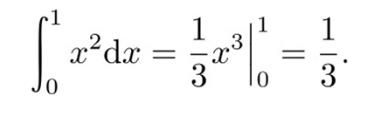
一桥飞架南北，天堑变通途。不管在现实生活中，还是在各色理论里，显然，没有人不喜欢桥梁。而FTIC的第一部分，则是我们可以搭梁建桥的原因。

本书作者还提到了如下观点：在积分学没有建立，甚至连积分的术语都不清不楚的时代，不管是牛顿还是莱布尼茨，都不可能建立微分和积分之间的联系。需要特别说明的是，这个观点并非语不惊人死不休，而同样是尊重历史的做法。我们不能否认牛顿、莱布尼茨的伟大，但也不能带着今天已经了然于心的知识储备穿越回他们的时代、进而评价他们的工作。怎样理解这种观点呢？我们不妨看一个具体的例子。因为有

现在我要说明，一般的求积问题可简化为寻找一条有特定相切规则的曲线。^[注释5]

这样一句话，莱布尼兹发表于1693的论文^[注释6]一直被公认为最早就积分学基本定理给出了证明。结合当时的时代背景、分析了莱布尼茨的论文后，荷兰乌得勒支大学的数学史学者维克托·布洛舍（Viktor Blåsjö）认为这是断章取义的做法，作者进而给出如下观点^[注释7]:

(i)尽管与积分学基本定理存在关联，尽管莱布尼茨对一般的面积求解问题感兴趣，但 1693年论文的基本出发点是牵引运动这样一个具体、特殊的问题；

(ii)涉及到多项式函数、指数函数、对数函数的求面积问题已被广泛地讨论，1693年的论文讨论的恰好是积分学基本定理不能使用的场景（若采用当代的记号，即 ）；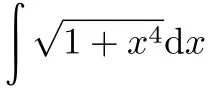

(iii)尽管“定义–定理–证明”的模式已经成为当代论证的基本模式，但莱布尼茨本人并不认为积分学基本定理是一个定理，自然也“不需要”一个证明；

出于这样新颖的观点，这篇论文被普林斯顿大学出版社收录在The Best Writing on Mathematics 2016中。

笔者仅就自己负责翻译的部分指出一点不足，作者在一些细节的处理上太在乎读者的感受，但在另外一些细节上处理得又不太够。一方面，在3.5节，引用李普曼·伯斯单调递增函数定理的证明之时，给定实数集合S，作者有意回避了上确界sup(S)这样令人望而生畏的专业术语，转而采用文字叙述，显然这是为了考虑读者的感受。但另一方面，在3.3节，对于大于1的底数a和充分小的正数ω，作者省略了欧拉给出的具体的演算实例，直接令aω=1+kω。在数学科普文章中，欧拉计算自然底数e的故事无疑是值得讲述的，但作者这种“武断的”做法不太容易让人接受。我们可以引用费尔南多·戈维亚（Fernando Gouvêa）在这本书的评论中发表的观点:

作者阐述数学的方式有点儿快，这个做法大大超过了本科生的接受能力。事实上这部书的真正受众应是那些讲授微积分课程的老师。

回想自己在大学时期对微积分的认知，再结合近几年教微积分的经历, 笔者大致认同这个观点。但话说回来，考虑到文理结合的通识课程正在被越来越广泛地提及，网络的普及使人们可以便捷地检索和查阅诸多优质的线上教学资源，我们依旧可以期待有兴趣的读者朋友能够从历史的角度去了解微积分那些惊心动魄的伟大时刻，去看看那些闪闪发光的公式、定理，去试着理解和把玩这些结果。这无疑是对刻板、严肃、以传统教科书的方式进行的课堂教学的极好补充。

本书的翻译在林开亮的提议和组织、叶卢庆的技术支持下，由三人通力合作而完成，其中：

叶卢庆负责第一章的翻译, 并提供了tex模板；

陈见柯负责第二、三章的翻译，以及全书的译稿统筹工作；

林开亮负责第四、五、六、七章的翻译。

在翻译过程中，我们与作者通过电子邮件进行了有效的沟通，作者也给予我们很多中肯的建议。我们要感谢人民邮电出版社北京图灵文化发展有限公司的编辑老师。我们在 2019 年年初接手这本书的中文翻译工作，预计交稿时间是一年后。出于各种原因，交稿日期一拖再拖，所幸最终付梓。笔者要向北京市朝阳区教育研究中心的张浩博士、中国矿业大学理学院的张汉雄博士和中国传媒大学经济与管理学院2018级齐嘉璐同学、数据科学与智能媒体学院 2018 级马行健同学, 感谢他们耐心地阅读了笔者负责翻译的部分，并提出宝贵的建议；感谢他们告知我们，于品教授、李逸教授都曾编写过数学分析的讲义。笔者也向中国传媒大学信息与通信工程学院的刘金波博士和2016级张锦皓同学表示感谢，感谢他们分别为笔者补充了电磁学和乐理的基本知识。

我们努力做到忠实于原著，也希望能够传达作者对于那些“大先生”所处时代的历史考证。但出于译者水平和修养所限，书稿中难免出现错误，还望读者朋友们不吝赐教，我们的邮箱地址是:

叶卢庆 [e-mail]

陈见柯 [e-mail]

林开亮 [e-mail]

2021年12月4日于十三陵

注释

[1] 它的英文术语标注为fundamental theorem of infinitesimal calculus。 

[2] 有些奇怪的是，在他们所有的表述中，都没有提及牛顿–莱布尼茨公式的说法。 

[3] 指FTIC中公式(1)及之前的部分。  

[4] 蒙李逸老师告知，2005年，清华大学出版社出版，徐森林、薛春华老师编著的《数学分析》就已经使用这样的说法了。 

[5] I shall now show that the general problem of quadratures can be reduced to the finding of a curve that has a given law of tangency. 

[6] Supplementum geometriae dimensoriae, seu generalissima omnium Tetragonismorum effectio per motum: similiterque multiplex constructio lineae ex data tangentium conditione. ” Acta Eruditorum. 385-392. 1693.  

[7] The Myth of Leibniz’s Proof of the Fundamental Theorem of Calculus.” Nieuw Archief voor Wiskunde. Series 5, Volume 16, Issue 1, 46-50. 2015.

  推荐阅读

作者：[美]戴维·M. 布雷苏（David M. Bressoud）

译者：陈见柯 林开亮 叶卢庆

美国数学协会推荐读物，汤涛院士推荐

一堂“新角度”微积分数学课，带你回溯微积分的起源与思想发展历程

前美国数学协会会长、《高等微积分》作者戴维•M.布雷苏最新数学科普作品