论文笔记：Multivariate Time-series Imputation with Disentangled Temporal Representations

Posted 2023-03-08 UQI-LIUWJ

ICLR 2023

1 Intro

• 多元时间序列补全的新模型
  • N个变量，时间跨度为T的多元时间序列，可以表示成
    • 这提供了两个视角以供补全
      • 建模变量间的关联性（cross-channel correlation）
      • 提取时间动态性
• 深度学习的方法大多基于RNN来建模多元时间序列
  • 但他们大多使用纠缠着的表征（entangled representation）【比如hidden state】来表征时间序列的动态
    • 但是在实际的时间序列中，他们的动态是由各种独立的因素组成的（比如趋势、周期性、残差项）
    • 使用entangled representaion可能不会得到好的补全效果
      • 因为entangled representation需要同时解释多个独立的、正交的pattern
• 这篇论文提出了TIDER（Time-series Imputation with Disentangled tEmporal Representations）
  • 将多元时间序列中复杂的动态关系，用解耦的表征分别建模时间序列的趋势、周期、局部残差项
  • 使用矩阵分解的框架，在长时间序列中更scalable
  • 同时，不同的解耦表征也给模型带来了可解释性

2 模型部分

2.1 整体部分

 

• 其中M 是一个mask 矩阵，表示哪些元素有观测值，哪些没有

   

  • 
• V_t是趋势特征矩阵
• V_s是周期特征矩阵
• V_b是残差特征矩阵

当这些低秩特征矩阵都学习完毕后，原来有观测值的位置保持不变，没有观测值的部分使用补全值

 2.2 趋势特征矩阵

• 建模时间序列的内部趋势
  • 希望是逐步的、平滑的变化
  • 将趋势特征矩阵的平滑度表示为

   

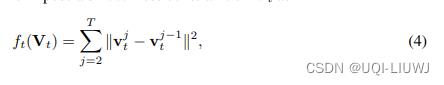
2.3 周期特征矩阵

使用傅里叶级数表示

其中： 

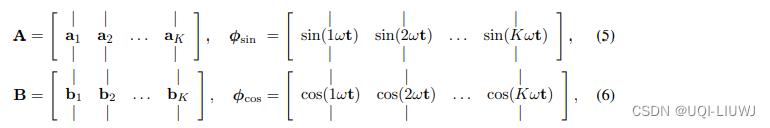
 这里ω是一个超参数

2.4 趋势特征矩阵

优点类似TRMF的自回归方式 

2.5 自适应权重

中的V改成：

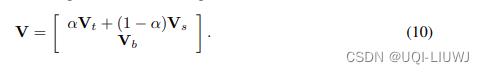
其中α是一个可学习的参数

3 实验 

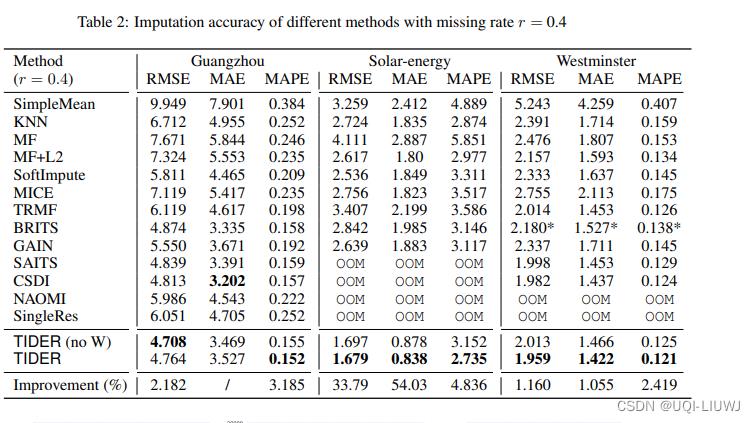
3.1 补全效果

 

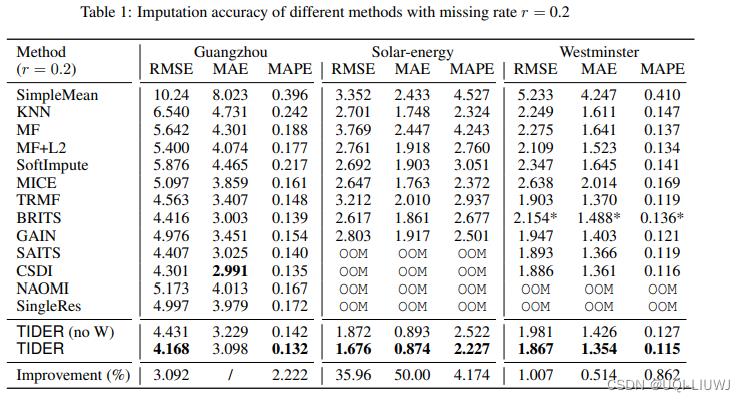
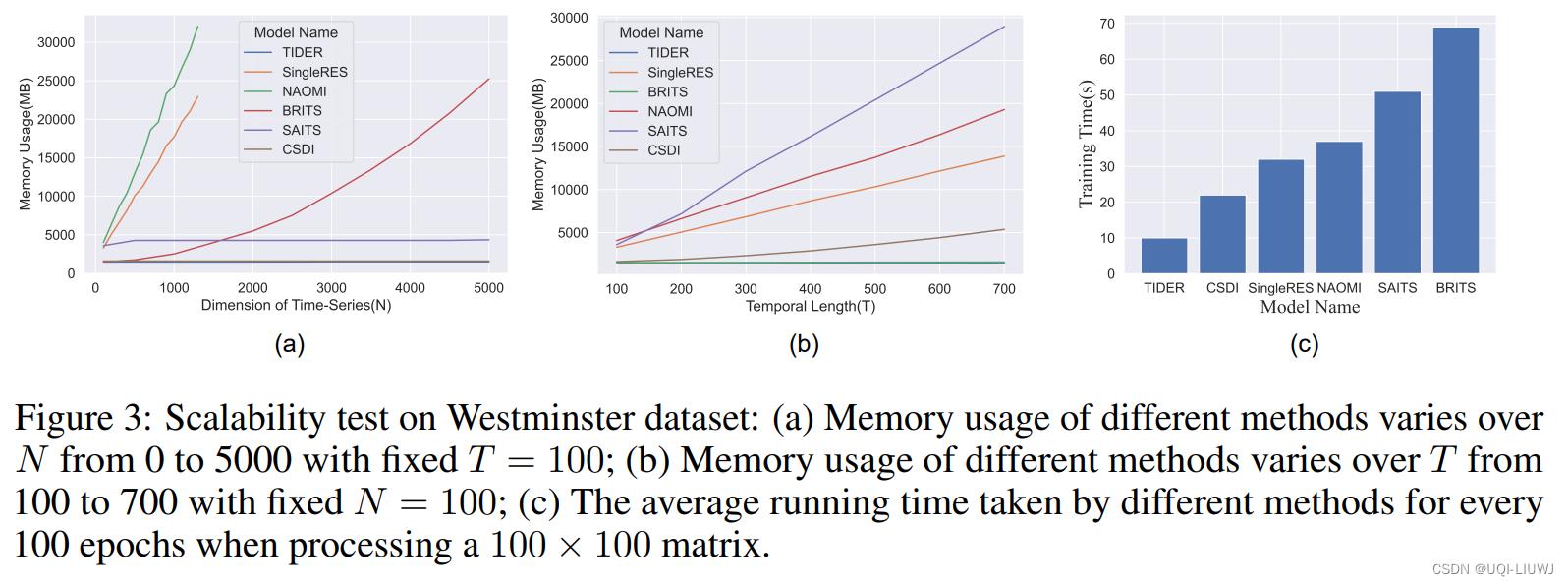
 3.2  scalability

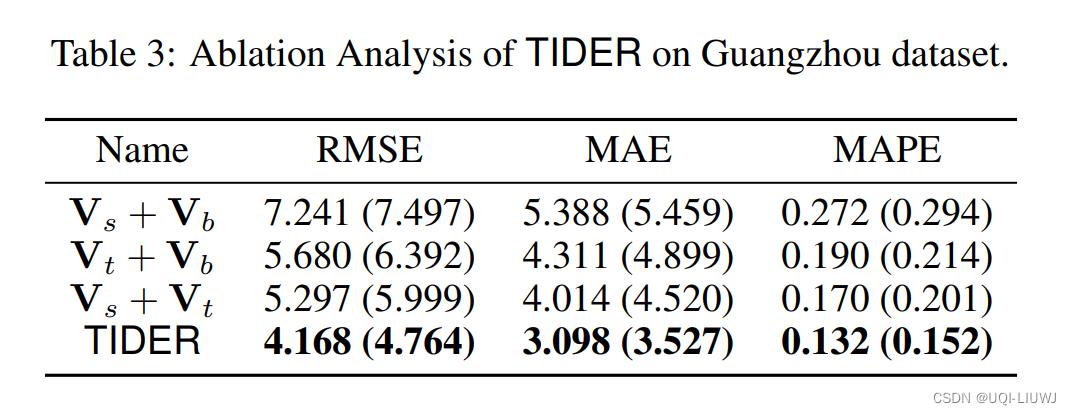
 3.3 Ablation

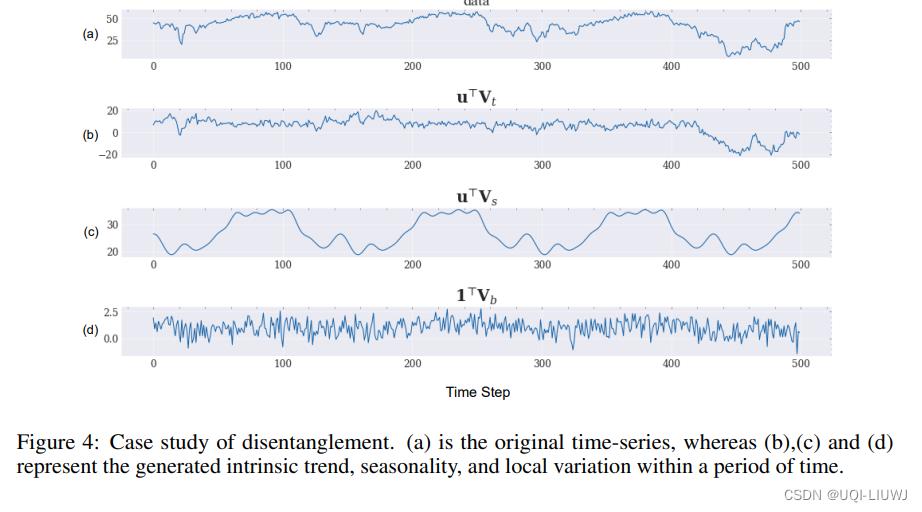
 3.4 Disentanglement 可视化