信号与系统 2023(春季) 作业要求 - 第二次作业
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了信号与系统 2023(春季) 作业要求 - 第二次作业相关的知识,希望对你有一定的参考价值。

01 基础练习
一、信号的直流分量
分别写出下面信号的直流分量与交流分量。
注: 交流分量可以使用原信号减去对应的直流分量来表示。
1、必做题
(1)全波整流信号
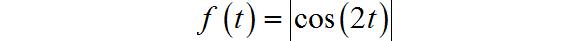
(2) 周期矩形信号

(3) 周期冲激信号
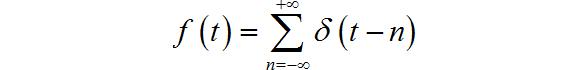
(4)非周期信号
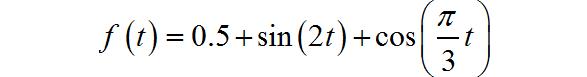
二、信号奇偶分解
1、必做题
(1) 奇偶分解
分别绘制出下面有限长信号与序列的奇分量与偶分量。
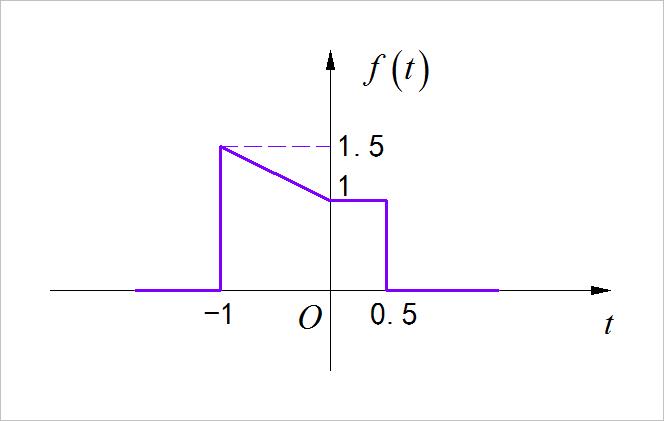
▲ 图1.2.1 连续时间信号
▲ 图1.2.2 离散序列信号
(2) 求解原信号波形
根据已知的信号 x ( t ) x\\left( t \\right) x(t) 偶分量与右半边波形, 绘制出原始信号 x ( t ) x\\left( t \\right) x(t) 的波形。

▲ 图1.2.3 信号的偶分量与信号的右半边波形
2、选做题
(1) 信号进行奇偶分解
绘制出下面连续时间信号与离散时间序列的奇分量与偶分量。
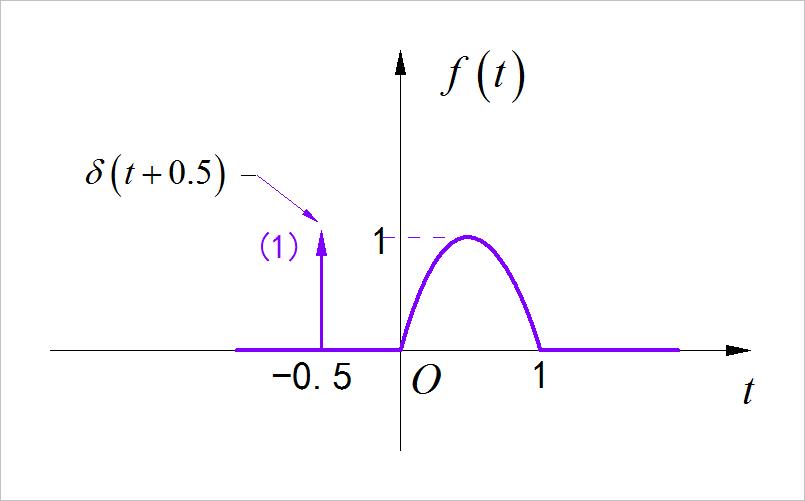
▲ 图1.2.4 连续时间信号
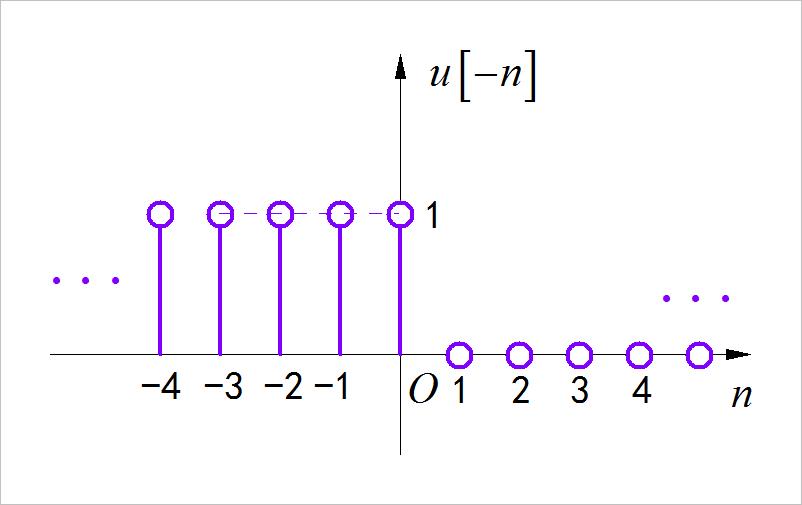
▲ 图1.2.5 反因果单位阶跃序列信号

三、信号尺度变换
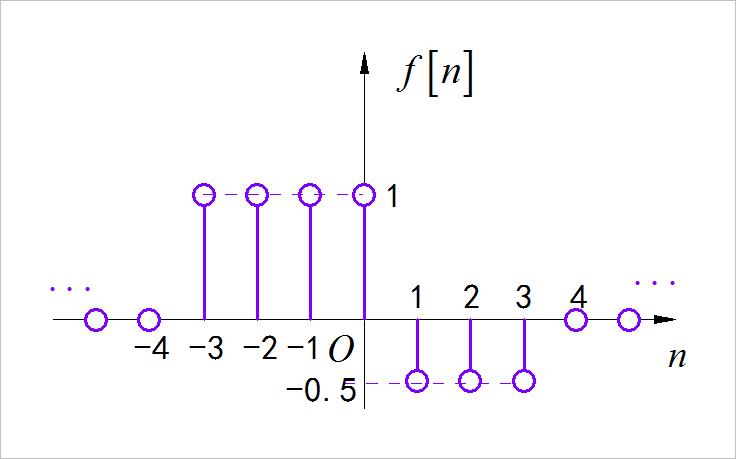
已知离散时间序列信号
f
[
n
]
f\\left[ n \\right]
f[n] 与连续时间信号
f
(
t
)
f\\left( t \\right)
f(t) 的波形如下图所示, 请根据后面给出的表达式绘制出对应自变量变化后的信号波形。

▲ 图1.3.1 离散时间序列与连续时间信号
1、必做题
(1)
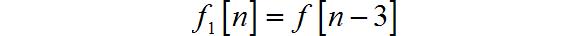
(2)
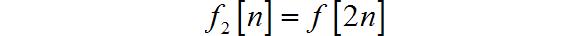
(3)

(4)
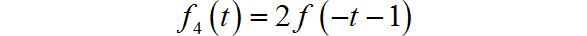
2、选做题
(1)
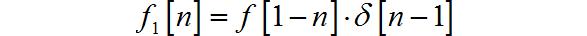
(2)
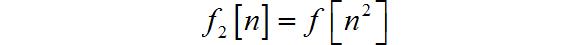
(3)
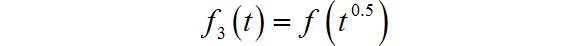
(4)

四、LTI系统响应
1、必做题
已知一个线性时不变(LTI)系统, 当激励为 e 1 ( t ) = u ( t ) e_1 \\left( t \\right) = u\\left( t \\right) e1(t)=u(t) 时, 对应的系统响应为 y 1 ( t ) = t 2 ⋅ e − 0.5 t ⋅ u ( t ) y_1 \\left( t \\right) = t^2 \\cdot e^ - 0.5t \\cdot u\\left( t \\right) y1(t)=t2⋅e−0.5t⋅u(t)
试求当激励为 e 2 ( t ) = δ ( t − 1 ) e_2 \\left( t \\right) = \\delta \\left( t - 1 \\right) e2(t)=δ(t−1) 时, 对应的系统相应 y 2 ( t ) y_2 \\left( t \\right) y2(t) 的表达式。
- 假定系统的起始条件为 0, 系统输入输出之间满足严格的线性关系。 本题需要利用线性时不变系统的微分特性与时不变特性。
2、选做题
Conside a LTI system whose response to the signal x 1 ( t ) x_1 \\left( t \\right) x1(t) in Figure (A) is the signal y 1 ( t ) y_1 \\left( t \\right) y1(t) illustrated in Figure (B). Determine and sketch carefully the response of the system to the input x 2 ( t ) x_2 \\left( t \\right) x2(t) and x 3 ( t ) x_3 \\left( t \\right) x3(t) illustrated in Figure (C ) and (D) respectively.
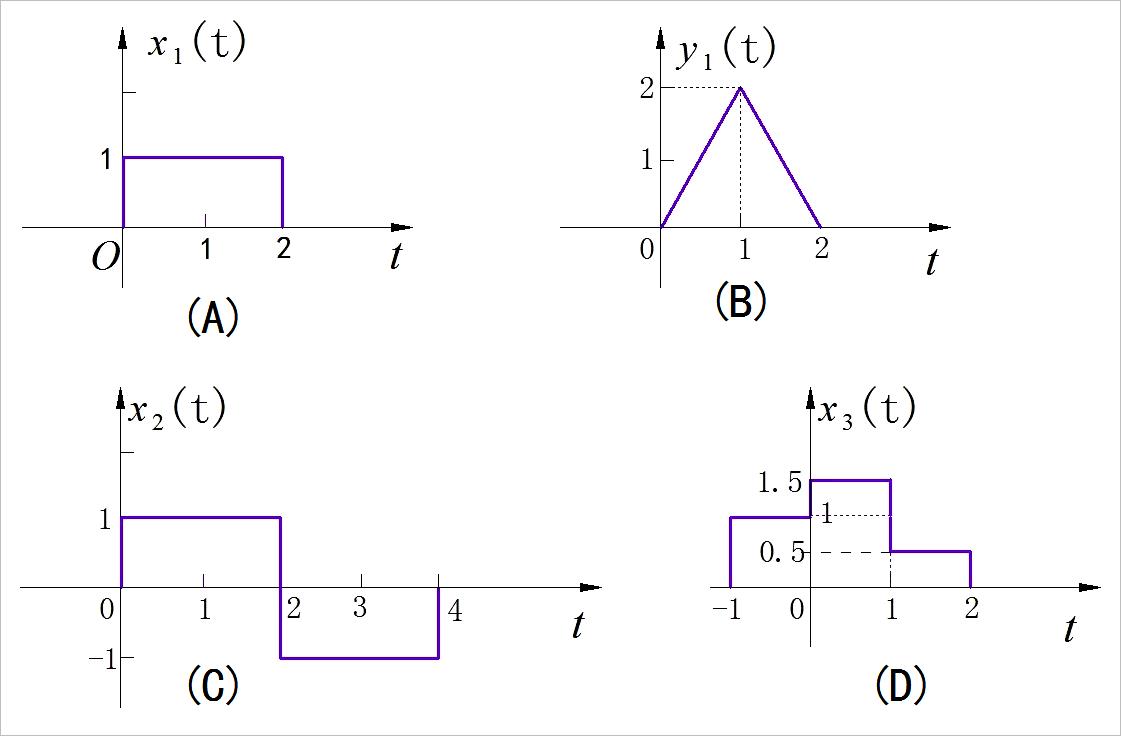
▲ 图1.4.1 LTI 系统输入输出信号
提示: 利用线性时不变系统特性求解此题。 将新的输入信号 x 2 ( t ) , x 3 ( t ) x_2 \\left( t \\right),x_3 \\left( t \\right) x2(t),x3(t) 分别表示成 x 1 ( t ) x_1 \\left( t \\right) x1(t) 与其时移信号的线性组合, 然后在根据 LTI 特性, 对应系统输出可以使用 y 1 ( t ) y_1 \\left( t \\right) y1(t) 和它的延时信号进行线组合而得。
五、系统的可逆性
判断下列系统是否可逆。 如果可逆则给出对应的逆系统。 如果不可逆, 则给出两个不同的输入信号,他们所引起系统的输出是相同的。
题目中, 输入信号为 e ( t ) , e [ n ] e\\left( t \\right),e\\left[ n \\right] e(t),e[n] , 输出信号为 r ( t ) , r [ n ] r\\left( t \\right),r\\left[ n \\right] r(t),r[n] 。
1、必做题
(1)
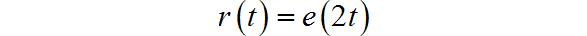
(2)
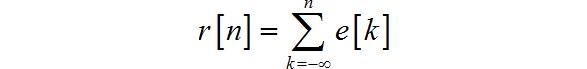
(3)
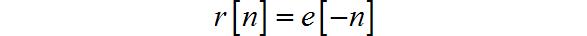
(4)

2、选做题
讨论下面电路输入输出之间是陈本可逆?
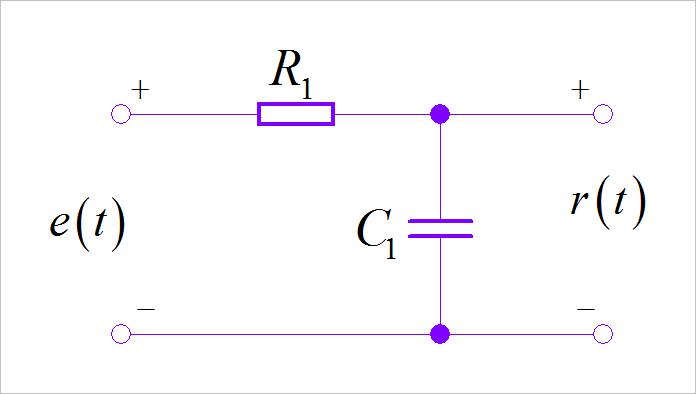
▲ 图1.5.1 低通滤波电路
- 提示: 参见博文 RC低通滤波器的逆系统
RC滤波器的逆系统
六、系统特性
1、必做题
根据下面表格描述系统的输入输出关系表达式, 分别判断系统的线性、时不变、因果 特性。
| 序号 | 系统输入输出关系 | 线性? | 时不变? | 因果? |
|---|---|---|---|---|
| 1 | r ( t ) = d d t e ( t ) r\\left( t \\right) = d \\over dte\\left( t \\right) r(t)=dtde(t) | |||
| 2 | r ( t ) = e ( t ) ⋅ u ( t ) r\\left( t \\right) = e\\left( t \\right) \\cdot u\\left( t \\right) r(t)=e(t)⋅u(t) | |||
| 3 | r ( t ) = e ( 1 − t ) r\\left( t \\right) = e\\left( 1 - t \\right) r(t)=e(1−t) | |||
| 4 | r ( t ) = e ( 3 t ) r\\left( t \\right) = e\\left( 3t \\right) r(t)=e(3t) | |||
| 5 | r ( t ) = e 2 ( t ) r\\left( t \\right) = e^2 \\left( t \\right) r(t)=e2(t)以上是关于信号与系统 2023(春季) 作业要求 - 第二次作业的主要内容,如果未能解决你的问题,请参考以下文章 |