2022年第十一届认证杯数学中国数学建模国际赛小美赛:C 题 对人类活动进行分类 建模方案及代码实现
Posted Better Bench
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2022年第十一届认证杯数学中国数学建模国际赛小美赛:C 题 对人类活动进行分类 建模方案及代码实现相关的知识,希望对你有一定的参考价值。
2022年第十一届认证杯数学中国数学建模国际赛小美赛:C 题 对人类活动进行分类 建模方案及代码实现

更新进展
(1)2022-12-3 10:00 发布合并后的数据,完整的python代码、LSTM建模方案
(2)2023-1-4 更新完所有代码,解决了bug
1 题目
人类行为理解的一个重要方面是对日常活动的识别和监控。可穿戴活动识别系统可以在许多关键领域提高生活质量,如门诊监测、居家康复、跌倒检测等。基于惯性传感器的活动识别系统通过个人报警系统[1]、跌倒检测和分类[2]、医疗诊断和治疗[3]、在家或学校远程监测儿童、康复和物理治疗、生物力学研究、人体工程学、体育科学、芭蕾舞和舞蹈、动画、电影制作、电视、现场娱乐、虚拟现实和电脑游戏[4]等应用于远程监测和观察老年人。我们尝试使用微型惯性传感器和定位于身体不同部位的磁力计来对人类活动进行分类,获得了以下数据。
这19项活动由8名受试者(4名女性,4名男性,年龄在20至30岁之间)进行,每项活动持续5分钟。每个受试者的每项活动信号总持续时间为5分钟。受试者被要求以自己的风格执行活动,不受活动应该如何执行的限制。因此,在一些活动的速度和幅度上存在着学科间的变化。
对传感器单元进行校准,以获取25赫兹采样频率的数据。5分钟的信号被分成5秒的片段,因此每个活动可获得480(= 60 × 8)个信号片段。
这19个活动是:
1.坐(A1);
2.站(A2);
3.仰卧(A3);
4.右侧卧(A4);
5.上升楼梯(A5);
6.下行楼梯(A6);
7.静止站在电梯里(A7);
8.在电梯里四处走动(A8);
9.在停车场散步(A9);
10.在跑步机上以4公里/小时的速度平卧和15度斜卧行走(A10);
11.在跑步机上以4公里/小时的速度以15度倾斜姿势行走(A11);
12.在跑步机上以8公里/小时的速度跑步(A12);
13.在步进机上锻炼(A13);
14.在交叉训练机上锻炼(A14);
15.水平骑健身自行车(A15);
16.以垂直姿势骑健身自行车(A16);
17.划船(第A17);
18.跳(A18);
19.打篮球(A19)。
要求你们队建立一个合理的数学模型来解决以下问题。
1.请设计一组特征和一个高效的算法,以便从这些穿戴式传感器的数据中对19种人类行为进行分类。
2.由于数据成本高,我们需要在有限的数据集下,使模型具有良好的泛化能力。我们需要对这个问题进行具体的研究和评估。请设计一个可行的方法来评估你的模型的泛化能力。
3.请研究并克服过拟合问题,让你的分类算法可以广泛应用于人的动作分类问题。
完整的数据可以通过以下链接下载:https://caiyun.139.com/m/i?0F5CJUOrpy8oq
附录:文件结构
19项活动(a)
8个科目§
60个片段
躯干(T),右臂(RA),左臂(LA),右腿(RL),左腿(LL) 5个单元
每个单元上有9个传感器(x, y, z加速度计,x, y, z陀螺仪,x, y, z磁力计)
文件夹a01, a02,…, a19包含19个活动记录的数据。
对于每个活动,子文件夹p1, p2,…, p8包含了这8个主题中的每一个的数据。
在每个子文件夹中,有60个文本文件s01, s02,…, s60,每个段一个。
在每个文本文件中,有5个单元× 9个传感器= 45列,5秒× 25赫兹= 125行。
每一列包含在5秒的时间内从其中一个单元的其中一个传感器获取的125个数据样本。
每一行包含在一个用逗号分隔的特定采样时刻从所有45个传感器轴获得的数据。
列1-45对应于:
T_xacc, T_yacc, T_zacc, T_xgyro,…, T_ymag, T_zmag,
RA_xacc, RA_yacc, RA_zacc, RA_xgyro,…, RA_ymag, RA_zmag,
LA_xacc, LA_yacc, LA_zacc, LA_xgyro,…, LA_ymag, LA_zmag,
RL_xacc, RL_yacc, RL_zacc, RL_xgyro,…, RL_ymag, RL_zmag,
LL_xacc, LL_yacc, LL_zacc, LL_xgyro,…, LL_ymag, LL_zmag。因此,1-9对应1号单元(T)的传感器,10-18对应2号单元(RA)的传感器,19-27对应3号单元(LA)的传感器,28-36对应4号单元(RL)的传感器,37-45对应5号单元(LL)的传感器。
2 思路解析
这是分类问题,大多数现成的模型是深度学习,主流的研究方向也是采用的深度学习。用机器学习的很少。当涉及到挖掘特征的时候,需要考虑的就是机器学习方法了。
1.请设计一组特征和一个高效的算法,以便从这些穿戴式传感器的数据中对19种人类行为进行分类。
解析:合并19个文件夹中的文件,对数据预处理,包括缺失值处理、数据归一化,滑动窗口设置。归一化的时候,注意
磁力计的数值远高于加速度计和陀螺仪的数值。如果我们用这些数据训练我们的网络,磁力计数据将比加速度计和陀螺仪具有更高的重要性。将所有传感器数据缩放在一起归一化会保持这种不平衡。单独对每种传感器的数据归一化,就是是重新缩放数据传感器,可以打破这种平衡。
2.由于数据成本高,我们需要在有限的数据集下,使模型具有良好的泛化能力。我们需要对这个问题进行具体的研究和评估。请设计一个可行的方法来评估你的模型的泛化能力。
提高模型的泛化能力。可以采用迁移学习,或者小样本学习中的元学习,都能在有限的样本内提高泛化能力。从四个角度出发
(1)从数据上提升性能
- 对数据做缩放(归一化,标准化等方法)
- 对数据做变换
- 特征选择(机器学习方法时采用)
(2)从算法上提升性能
- 算法的筛选(采用不同的分类模型)
- 重采样的方法(k折交叉验证、分层采样划分)
(3)从算法调优上提升性能
深度学习模型采用一下方法
- 模型可诊断性
- 权重的初始化
- 学习率
- 激活函数
- 网络结构
- batch和epoch
- 正则项
- 优化目标
- 提早结束训练
机器学习模型采用调参,可以考虑网格调参法。
(4)从模型融合上提升性能
- Bagging
- stacking
3.请研究并克服过拟合问题,让你的分类算法可以广泛应用于人的动作分类问题。
(1)数据集角度
- 增加样本量,数据集扩增
- 原有数据加随机噪声
- 重采样
(2)特征角度
- 特征选择
- 特征降维
(3)模型角度
- 降低模型复杂度
正则化 ,正则化正是通过在损失函数上添加额外的参数稀疏性惩罚项(正则项),来限制网络的稀疏性,以此约束网络的实际容量,从而防止模型出现过拟合。L1正则化是将权值的绝对值之和加入损失函数,使得权值中0值比重增大,因此得到的权值较为稀疏。L2正则化是将权重的平方之和加入损失函数,使得权值分布更加平均,所以权值较为平滑。
Dropout舍弃,在深度学习网络的训练过程中,对于神经网络单元,按照一定的概率将其暂时从网络中丢弃,使得每次训练的网络结构多样。
(4)训练角度
-
早停止,如在训练中多次迭代后发现模型性能没有显著提高就停止训练
-
交叉验证
2 python代码实现
2.1 数据分析
(1)数据集分析
data下有19个文件夹,分表表示19个活动,如a01,a01文件夹下有8个文件夹,表示8种科目,如p1,p1下有60个txt文件。表示60个片段。
其中每个txt文件中的格式如下
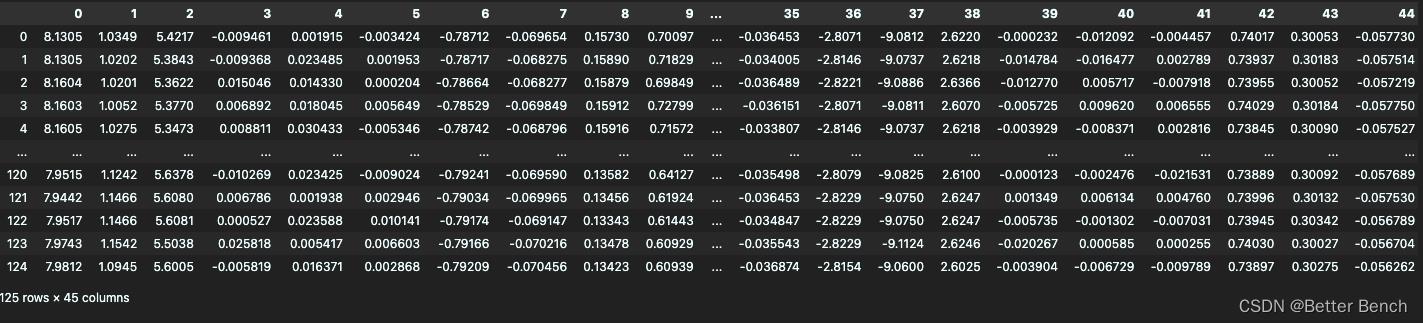
有125行,45列。总共费时5秒,一秒25赫兹的速度采集样本,得到5×25行的数据。45列表示身体放置有5个部位的设备,每种设备中有三个传感器,分别是加速度计、陀螺仪和磁力计,每个传感器有x,y,z三个坐标,就得到3×3×5 = 45列。
(2)读取文件分析
以19个动作分类,合并所有文件
import os
import pandas as pd
path = "data" #文件夹目录
files= os.listdir(path) #得到文件夹下的所有文件名称
s = []
all_txt = []
label = []
for A in files: #遍历文件夹
P_path= path+'/'+A
if os.path.isdir(P_path): #判断是文件夹,是文件夹才打开
P= os.listdir(path+'/'+A)
for s in P:
S_path= path+'/'+A+'/'+s
if os.path.isdir(S_path): #判断是文件夹,是文件夹才打开
S= os.listdir(path+'/'+A+'/'+s)
for t in S:
txtpath =path+'/'+A+'/'+s+'/'+t
。。。略
all_txt.append(txtfile)
label.extend([A]*len(txtfile))
data = pd.concat(all_txt, axis=0)
cols_str = 'T_xacc1,T_yacc1,T_zacc1,T_xacc2,T_yacc2,T_zacc2,T_xacc3,T_yacc3,T_zacc3,\\
RA_xgyro1,RA_ymag1,RA_zmag1,RA_xgyro2,RA_ymag2,RA_zmag2,RA_xgyro3,RA_ymag3,RA_zmag3,\\
LA_xgyro1,LA_ymag1,LA_zmag1,LA_xgyro2,LA_ymag2,LA_zmag2,LA_xgyro3,LA_ymag3,LA_zmag3,\\
RL_xgyro1,RL_ymag1,RL_zmag1,RL_xgyro2,RL_ymag2,RL_zmag2,RL_xgyro3,RL_ymag3,RL_zmag3,\\
LL_xgyro1,LL_ymag1,LL_zmag1,LL_xgyro2,LL_ymag2,LL_zmag2,LL_xgyro3,LL_ymag3,LL_zmag3'
cols = cols_str.split(',')
data.columns = cols
....
分析总数据集
import pandas as pd
data = pd.read_csv('data/all_txt.csv')
data
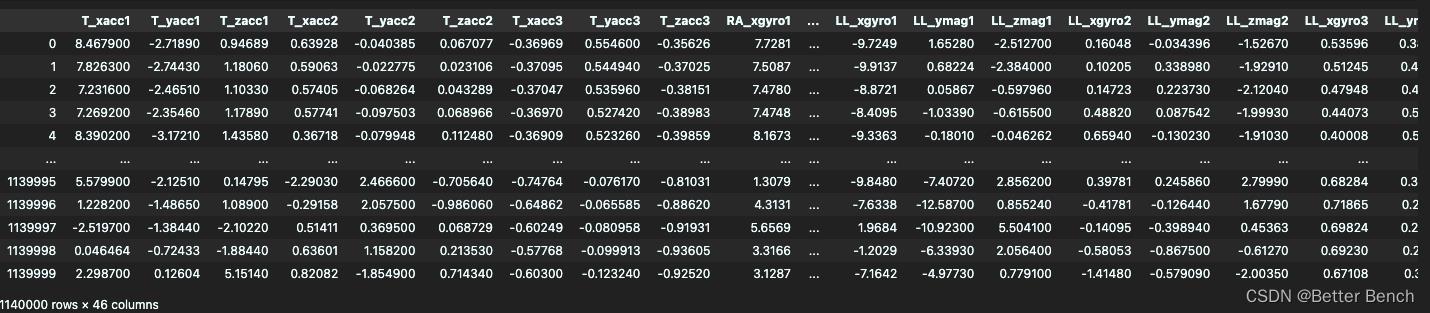
分析标签的分布
import matplotlib.pyplot as plt
x_axis = dict(data.label.value_counts()).keys()
y_axis = dict(data.label.value_counts()).values()
plt.figure(figsize=(12, 5))
plt.bar(x_axis, y_axis, width=0.5)
plt.xlabel('Activity label')
plt.ylabel('Count')
plt.title('Label Distribution')
plt.show()

查看是否 有缺失值
data.isnull().any().value_counts()
False 46 dtype: int64
无缺失值
2.2 数据预处理
(1)归一化
数据归一化,归一化的有两种,在每个标签的样本中逐个归一化,或者在整个数据集中归一化。对比一下归一化效果
def plot_data(y,title):
plt.figure(figsize=(15, 10))
x = range(len(y))
if isinstance(y, pd.DataFrame):
y1 = list(y.iloc[:,0])
y2 = list(y.iloc[:,1])
y3 = list(y.iloc[:,2])
else:
y1 = list(y[:,0])
y2 = list(y[:,1])
y3 = list(y[:,2])
plt.plot(x, y1)
plt.plot(x, y2)
plt.plot(x, y3)
plt.title(f'title')
plt.show()
原始数据中挑第一个传感器的x,y,z可视化
# 原始数据
plot_data(data,'origin dataset')
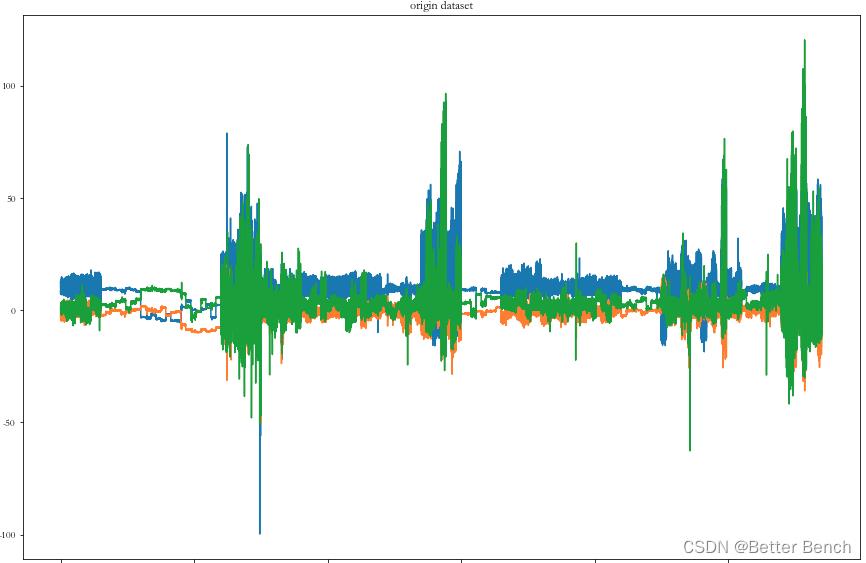
两种 不同方式的归一化后可视化分析
from sklearn.preprocessing import MinMaxScaler
import pandas as pd
scaler = MinMaxScaler(feature_range=[-1,1])
data_activity_wise =
data_activity_wise_scaled = []
all_activites = pd.unique(pd.Series(data.iloc[:, -1]))
for activity in all_activites:
data_activity_wise[activity] = data[data.iloc[:, -1] == activity]
import numpy as np
for activity, activity_data in data_activity_wise.items():
data_activity_wise_scaled.append(scaler.fit_transform(activity_data.iloc[:,0:-1]))
scaled_data = scaler.fit_transform(data.iloc[:, 0:-1])
data_scaled_at_once = np.concatenate((scaled_data, data.iloc[:, -1][:, None]), axis=1)
data_activity_wise2 = np.concatenate(data_activity_wise_scaled)
# 第一种归一化方式
plot_data(data_scaled_at_once[:, 0:3], "Scaled at once")
# 第二种归一化方式
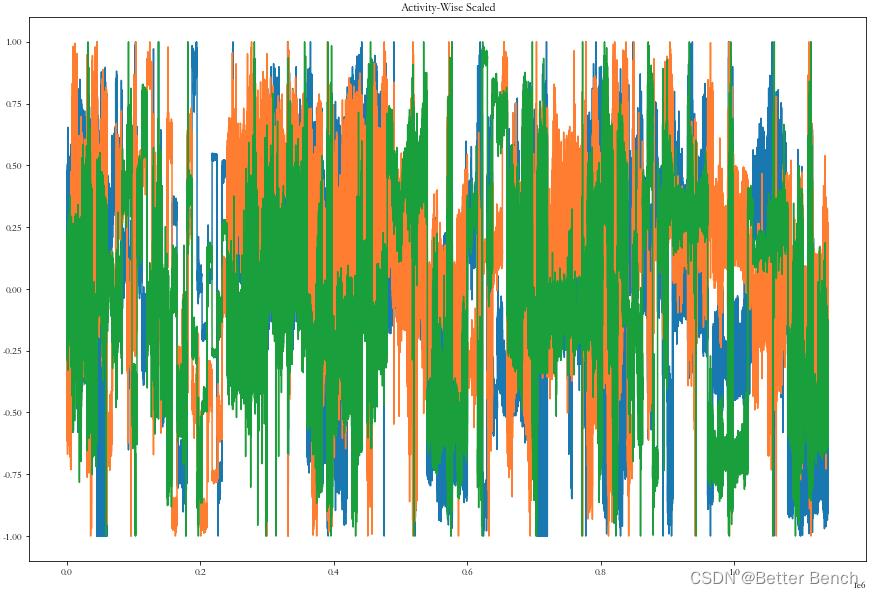
plot_data(data_activity_wise2, 'Activity-Wise Scaled')
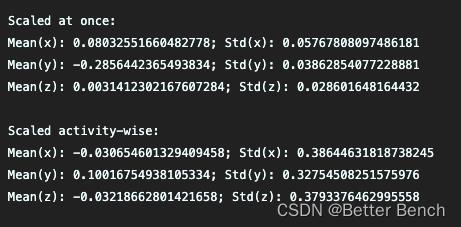
print("Scaled at once:")
print("Mean(x): " + str(np.mean(data_scaled_at_once[:, 1])) + "; Std(x): " + str(np.std(data_scaled_at_once[:, 1])))
print("Mean(y): " + str(np.mean(data_scaled_at_once[:, 2])) + "; Std(y): " + str(np.std(data_scaled_at_once[:, 2])))
print("Mean(z): " + str(np.mean(data_scaled_at_once[:, 3])) + "; Std(z): " + str(np.std(data_scaled_at_once[:, 3])))
print("\\nScaled activity-wise:")
print("Mean(x): " + str(np.mean(data_activity_wise2[:, 0])) + "; Std(x): " + str(np.std(data_activity_wise2[:, 0])))
print("Mean(y): " + str(np.mean(data_activity_wise2[:, 1])) + "; Std(y): " + str(np.std(data_activity_wise2[:, 1])))
print("Mean(z): " + str(np.mean(data_activity_wise2[:, 2])) + "; Std(z): " + str(np.std(data_activity_wise2[:, 2])))

对数据归一化后设置滑动窗口
注意:这里采用了方法二,因为简单。但是磁力计的数值远高于加速度计和陀螺仪的数值。如果我们用这些数据训练我们的网络,磁力计数据将比加速度计和陀螺仪具有更高的重要性。将所有传感器数据缩放在一起归一化会保持这种不平衡。方法一的归一化方法是重新缩放数据传感器,可以打破这种平衡。在改进的时候,可以对比讨论一下,丰富论文的实验内容。
from sklearn.model_selection import StratifiedShuffleSplit
# 归一化
scaled_data = scaler.fit_transform(data.iloc[:, 0:-1])
data_scaled_at_once = np.concatenate((scaled_data, data.iloc[:, -1][:, None]), axis=1)
# 层次划分训练集和验证集
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, valid_index in split.split(scaled_data,data.iloc[:, -1]):
train_data = data_scaled_at_once[train_index,:]
valid_data = data_scaled_at_once[valid_index,:] # 保证测试集
(2)设置滑动窗口,封装数据集
import numpy as np
def sliding_window_seconds(data, length_in_seconds=1, sampling_rate=50, overlap_ratio=None):
"""
Return a sliding window measured in seconds over a data array.
:param data: input array, can be numpy or pandas dataframe
:param length_in_seconds: window length as seconds
:param sampling_rate: sampling rate in hertz as integer value
:param overlap_ratio: overlap is meant as percentage and should be an integer value
:return: tuple of windows and indices
"""
windows = []
indices = []
curr = 0
overlapping_elements = 0
win_len = int(length_in_seconds * sampling_rate)
if overlap_ratio is not None:
overlapping_elements = int((overlap_ratio / 100) * win_len)
if overlapping_elements >= win_len:
print('Number of overlapping elements exceeds window size.')
return
while curr < len(data) - win_len:
windows.append(data[curr:curr + win_len])
indices.append([curr, curr + win_len])
curr = curr + win_len - overlapping_elements
return np.array(windows), np.array(indices)
def sliding_window_samples(data, samples_per_window, overlap_ratio):
"""
Return a sliding window measured in number of samples over a data array.
:param data: input array, can be numpy or pandas dataframe
:param samples_per_window: window length as number of samples per window
:param overlap_ratio: overlap is meant as percentage and should be an integer value
:return: tuple of windows and indices
"""
windows = []
indices = []
curr = 0
win_len = int(samples_per_window)
if overlap_ratio is not None:
overlapping_elements = int((overlap_ratio / 100) * (win_len))
if overlapping_elements >= win_len:
print('Number of overlapping elements exceeds window size.')
return
while curr < len(data) - win_len:
windows.append(data[curr:curr + win_len])
indices.append([curr, curr + win_len])
curr = curr + win_len - overlapping_elements
try:
result_windows = np.array(windows)
result_indices = np.array(indices)
except:
result_windows = np.empty(shape=(len(windows), win_len, data.shape[1]), dtype=object)
result_indices = np.array(indices)
for i in range(0, len(windows)):
result_windows[i] = windows[i]
result_indices[i] = indices[i]
return result_windows, result_indices
def apply_sliding_window(data_x, data_y, sliding_window_size, unit, sampling_rate, sliding_window_overlap):
"""
Function which transforms a dataset into windows of a specific size and overlap.
:param data_x: numpy float array
Array containing the features (can be 2D)
:param data_y: numpy float array
Array containing the corresponding labels to the dataset (is 1D)
:param sliding_window_size: integer or float
Size of each window (either in seconds or units)
:param unit: string, ['units', 'seconds']
Unit in which the sliding window is measured
:param sampling_rate: integer
Number of hertz in which the dataset is sampled
:param sliding_window_overlap: integer
Amount of overlap between the sliding windows (measured in percentage, e.g. 20 is 20%)
:return:
"""
output_x = None
output_y = None
if unit == 'units':
tmp_x, _ = sliding_window_samples(data_x, sliding_window_size, sliding_window_overlap)
tmp_y, _ = sliding_window_samples(data_y, sliding_window_size, sliding_window_overlap)
elif unit == 'seconds':
tmp_x, _ = sliding_window_seconds(data_x, sliding_window_size, sampling_rate, sliding_window_overlap)
tmp_y, _ = sliding_window_seconds(data_y, sliding_window_size, sampling_rate, sliding_window_overlap)
output_x = tmp_x
output_y = tmp_y
output_y = [[i[-1]] for i in output_y]
return output_x, np.array(output_y).flatten()
# settings for the sliding window (change them if you want to!)
sw_length = 50
sw_unit = 'units'
sw_overlap = 50
# apply a sliding window on top of both the train and validation data; you can use our predefined method
# you can import it via from preprocessing.sliding_window import apply_sliding_window
X_train, y_train = apply_sliding_window(train_data.iloc[:, :-1], train_data.iloc[:, -1], sliding_window_size=sw_length, unit=sw_unit, sampling_rate=50, sliding_window_overlap=sw_overlap)
X_valid, y_valid = apply_sliding_window(valid_data.iloc[:, :-1], valid_data.iloc[:, -1], sliding_window_size=sw_length, unit=sw_unit, sampling_rate=50, sliding_window_overlap=sw_overlap)
2.3 模型训练
(1)采用LSTM,框架是Pytorch。定义LSTM网络结构
from torch import nn
class DeepConvLSTM(nn.Module):
def __init__(self, config):
super(DeepConvLSTM, self).__init__()
# parameters
self.window_size = config['window_size']
self.drop_prob = config['drop_prob']
self.nb_channels = config['nb_channels']
self.nb_classes = config['nb_classes'以上是关于2022年第十一届认证杯数学中国数学建模国际赛小美赛:C 题 对人类活动进行分类 建模方案及代码实现的主要内容,如果未能解决你的问题,请参考以下文章