import torchvision
train_set = torchvision.datasets.MNIST(root='../dataset/mnist', train=True,  download=True)
test_set  = torchvision.datasets.MNIST(root='../dataset/mnist', train=False, download=True)

这段代码中，包括两个参数：root和train，download为可选参数。root指定数据集下载的根目录，train指定要加载的数据集类型，train=True表示加载训练集，train=False表示加载测试集。download=True表示如果本地不存在则进行该数据集的下载，最后将训练集和测试集分别保存在train_set和test_set两个变量中。

1.2 CIFAR-10数据集

CIFAR-10是一个常用的图像分类数据集，由10个不同类别的60000个32x32彩色图像组成。这些类别包括：飞机、汽车、鸟、猫、鹿、狗、青蛙、马、船和卡车。数据集被分为训练集和测试集，其中训练集包含50000个图像，测试集包含10000个图像。CIFAR-10数据集被广泛用于计算机视觉和深度学习研究领域，特别是用于图像分类算法的开发和测试。

import torchvision
train_set = torchvision.datasets.CIFAR10(…)
test_set  = torchvision.datasets.CIFAR10(…)

2 课堂内容

2.1 回归任务和分类任务的区别

回归任务和分类任务是机器学习中两个重要的任务类型，其主要区别在于预测目标的不同。分类任务的目标是将输入数据分到预定义的类别中。例如，手写数字分类任务中，目标是将手写数字图像分到0-9十个数字中的一个类别中。回归任务的目标是预测连续的数值。例如，房价预测任务中，目标是预测房屋的售价，这是一个连续的数值。

因此，回归任务和分类任务的主要区别在于预测目标的类型：分类任务的目标是预测一个离散的类别，而回归任务的目标是预测一个连续的数值。

2.2 为什么使用逻辑斯蒂回归

对于分类问题，由于值是离散的，所以用逻辑斯蒂回归(logistic regression)。二分类问题中，我们需要求得结果是 输入数据 所属的类别。例如下图，结果要么通过要么不通过，属于典型的二分类(binary classification)问题。

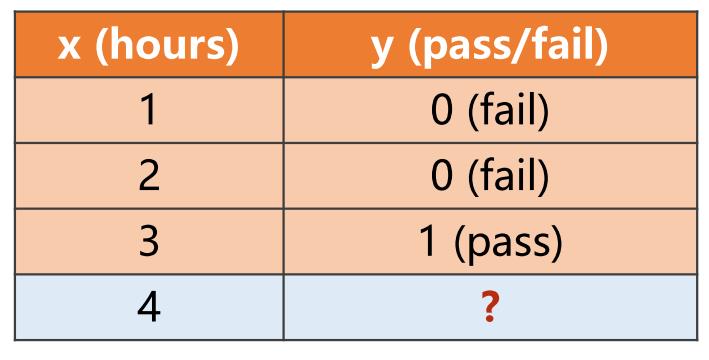
二分类问题是机器学习中最常见的问题之一，应用广泛，例如判断一封邮件是否是垃圾邮件、判断一个人是否患有某种疾病等。

2.3 什么是逻辑斯蒂回归

在二分类问题中，我们衡量输入的数据运算过后的所属类别的方法，一般是通过概率来表示，我们得到对应类别的概率值，哪个概率值大，就认为它是属于哪个类别。

Logistic回归是一种用于二分类问题的线性分类模型。它的基本思想是，将输入特征和对应的类别之间的关系建模为一个线性函数，并通过Sigmoid函数将其映射到[0,1]的区间上，以得到对应于正例的概率，所以可以说sigmoid函数的作用是使数据映射到[0,1]区间上。

2.4 Sigmoid函数和饱和函数的概念

在数学中，饱和函数（Saturated Function）是一类函数，当输入值接近正或负无穷时，函数的输出值趋向于一个有限的上下限。饱和函数通常用于神经网络的激活函数，例如Sigmoid函数

当输入值x的绝对值很大时，Sigmoid函数的输出值会趋近于0或1，因此称为“饱和函数”。

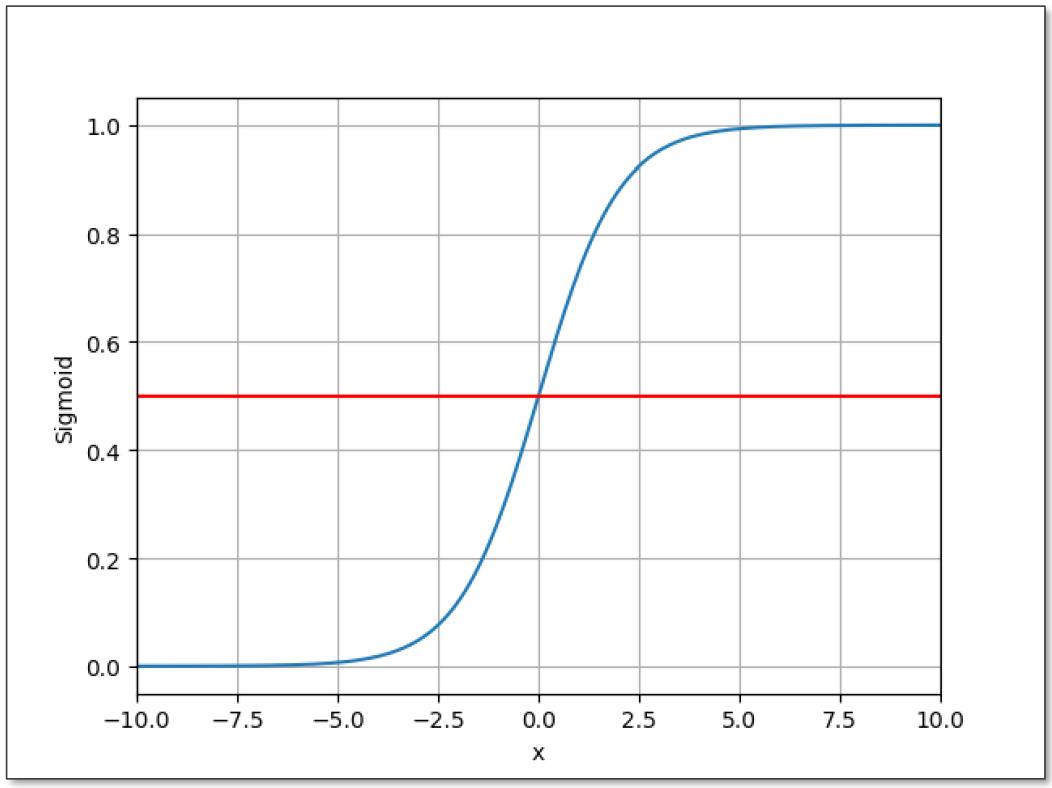
Sigmoid 函数在输入为负无穷时，输出为 0，在输入为正无穷时，输出为 1，因此可以将预测结果解释为概率值，并进行阈值分类。

在神经网络中，饱和函数作为激活函数具有平滑、可导的性质，并能够将输出值限制在一定范围内，使神经网络的训练更加稳定。但是，由于饱和函数在梯度计算时可能会出现梯度消失的问题，因此在深度神经网络中，更常使用一些非饱和函数作为激活函数，例如ReLU函数。

常见的Sigmoid函数还有：

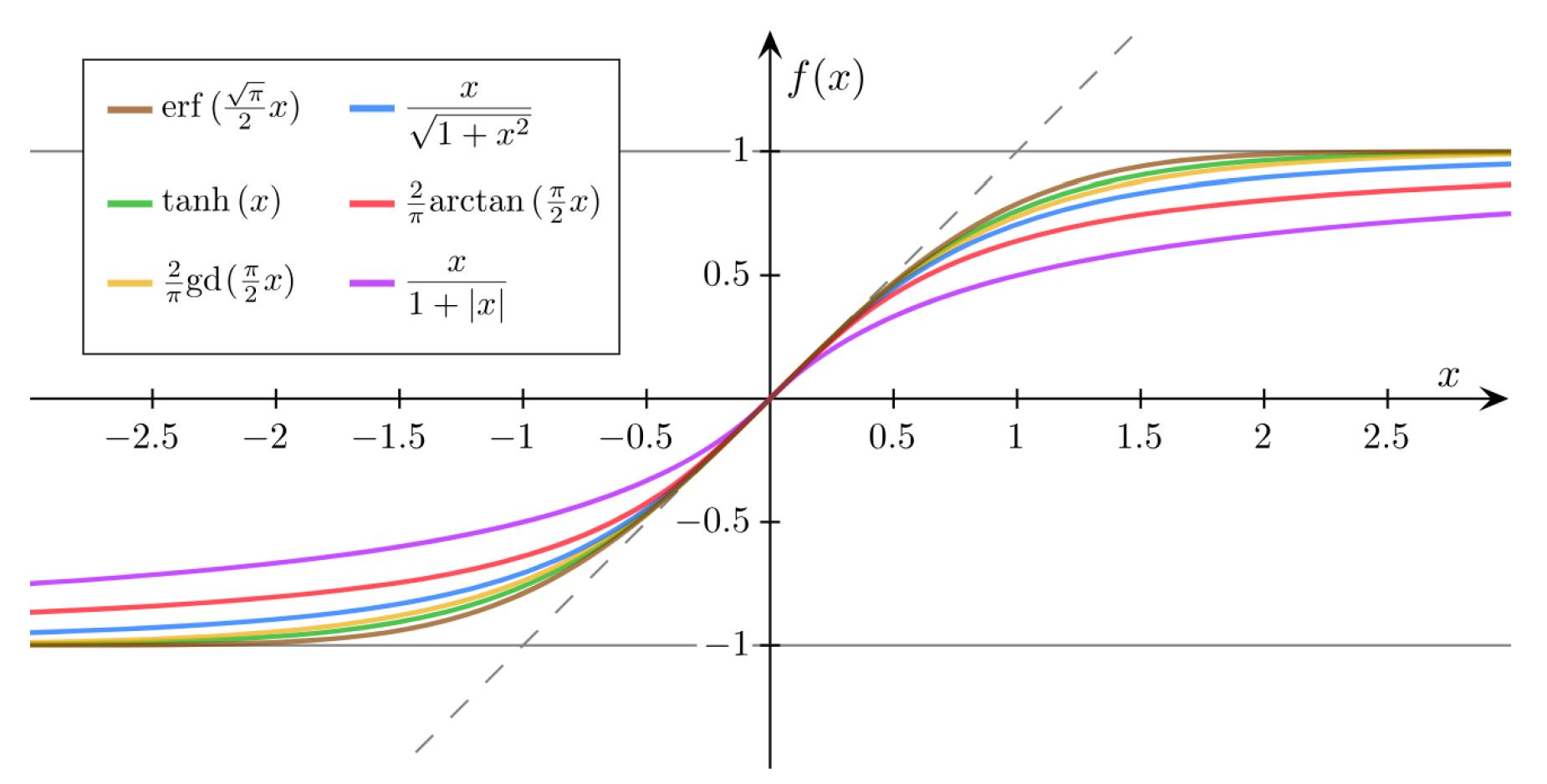
2.5 逻辑斯蒂回归模型

添加完logistic函数后的模型相较于普通的线性回归模型的变化：

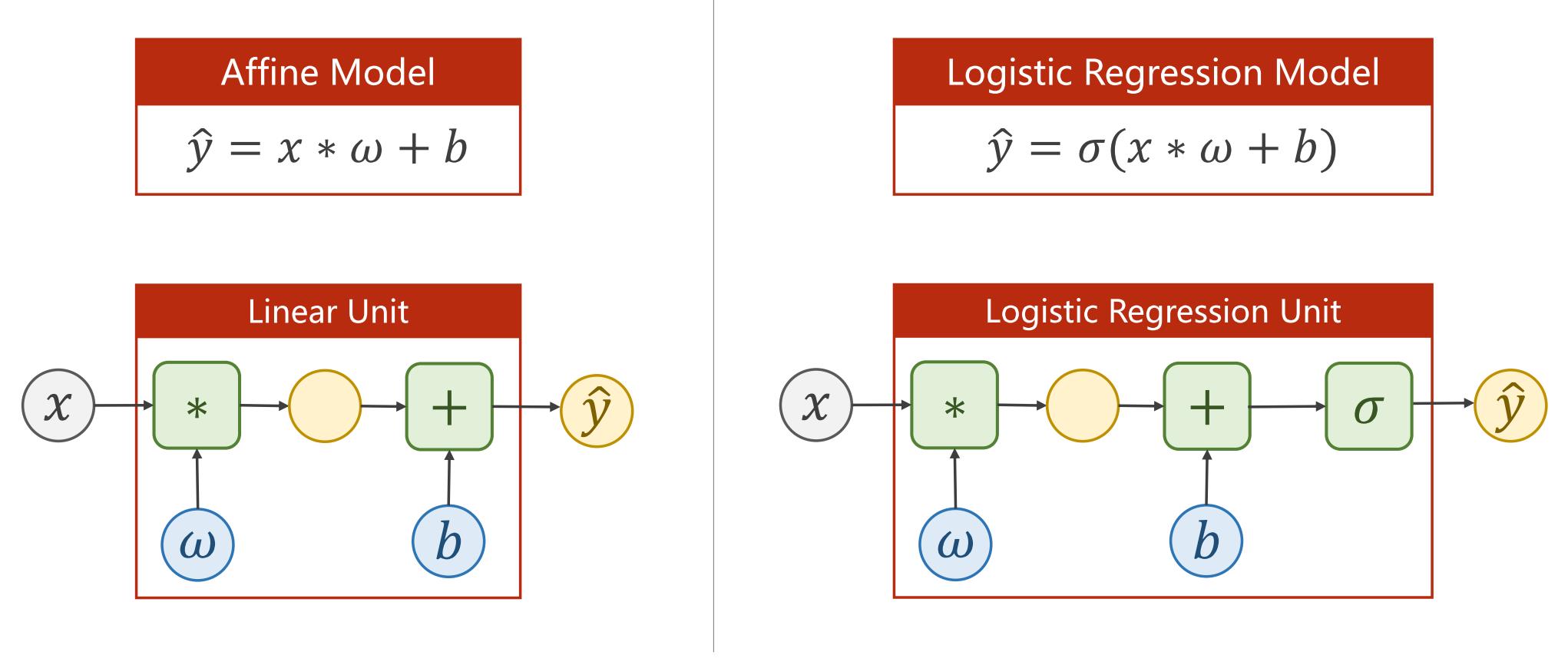
2.6 逻辑斯蒂回归损失函数

2.6.1 二分类交叉熵损失函数

二分类交叉熵损失函数(Binary Cross Entropy, BCE)较线性回归的损失函数也发生了些许变化，主要是引入了交叉熵(Cross Entropy)这个概念。交叉熵是在给定一组真实标签和一组预测标签的情况下，衡量这两组标签之间的差异的一种方法。

二分类交叉熵是指特定于二元分类任务而设计的交叉熵损失函数。对于二元分类问题，二分类交叉熵损失函数可以表示为：

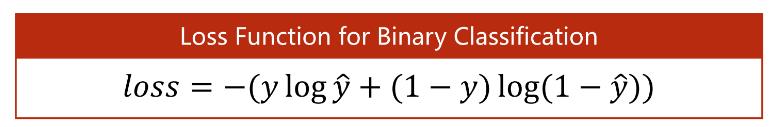
其中，y表示样本的真实标签（0或1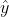），表示样本的预测标签（取值范围为[0, 1]）。

交叉熵损失函数的基本思想是：将真实标签和预测标签的概率分布进行比较，计算它们之间的差距，用来衡量预测标签和真实标签之间的相似度。当预测标签与真实标签越相似时，损失函数的值越小，反之，损失函数的值越大。

对于二分类问题而言，交叉熵损失函数可以解释为：如果样本的真实标签为1，那么我们希望模型预测标签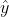的值越接近1越好；如果样本的真实标签为0，那么我们希望模型预测标签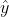的值越接近0越好。因此，交叉熵损失函数可以作为衡量二分类模型预测效果的重要指标。

BCE和MSE的区别？

BCE主要应用于二元分类问题，它的损失函数形式简单，可以直接衡量模型对于每个样本预测出的概率值和真实标签之间的差距。而 MSE 更适合用于回归问题，它可以衡量模型对于每个样本预测出的数值和真实值之间的差距。

2.6.2 小批量二分类损失函数

在实际应用中，我们通常需要对大规模数据集进行训练。如果使用全量数据计算梯度，会占用过多的内存和计算资源，从而导致训练速度缓慢或者无法完成训练。而使用小批量的BCELoss，可以将数据集分批次读入内存，逐个小批量地计算损失函数，进而计算梯度，从而加快训练速度，同时还能够有效降低内存使用和计算复杂度。

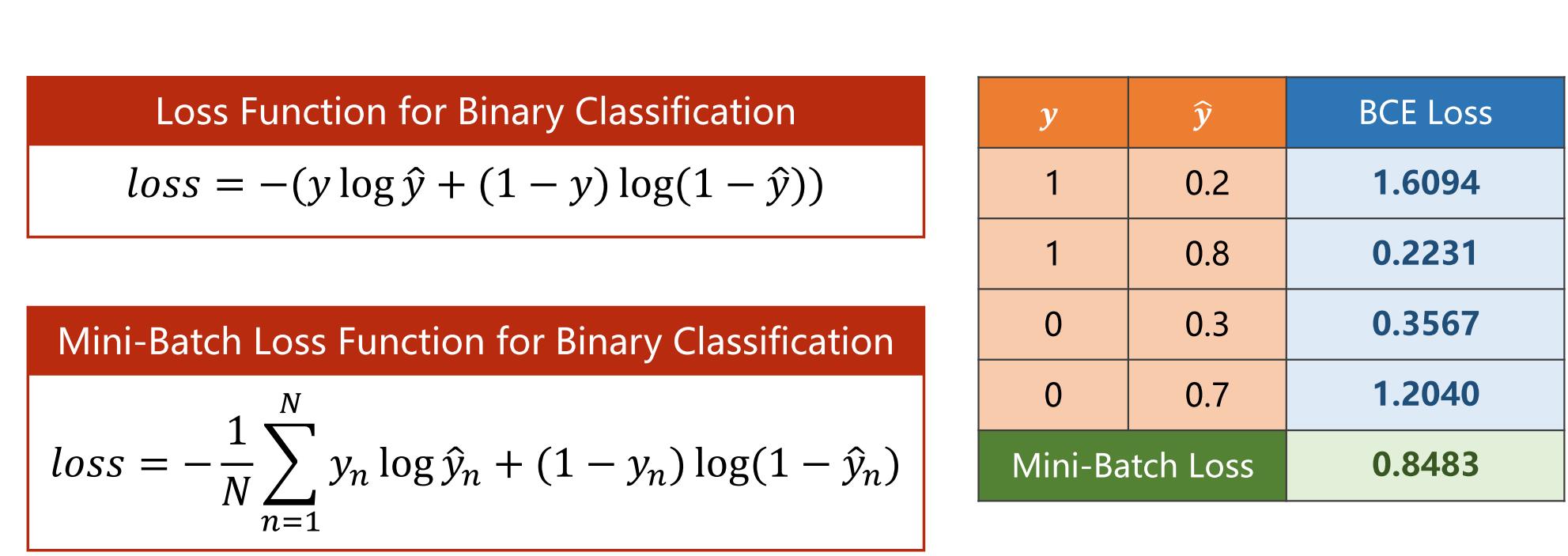
如果模型的预测值越接近真实值，交叉熵的损失就越小。因此，通过最小化交叉熵损失，我们可以训练一个能够准确分类数据的模型。

3 代码实现

1、这段代码定义了一个 logistic 回归模型类 LogisticRegressionModel，继承了 Module 类。该模型使用单个线性层（Linear）来预测输入 x 的输出。

class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)

    def forward(self, x):
        y_pred = F.sigmoid(self.linear(x)) # sigmoid 函数将输入值压缩到 [0,1] 的区间内，可以将线性层的输出转换为概率值，用于二分类问题的预测。
        return y_pred

2、定义一个二分类交叉熵损失函数对象，并将其赋值给变量criterion：

criterion = torch.nn.BCELoss (size_average=False)

在PyTorch中，torch.nn.BCELoss是二分类交叉熵损失函数的实现，它用于度量模型输出与真实标签之间的差异，其返回值即为模型的损失值。size_average参数表示是否对每个batch的损失值求平均，默认为True，如果设为False，则不求平均，返回的是每个batch的总和。因为我们一般在训练神经网络时，采用小批量梯度下降法，因此需要对每个小批量的损失值求平均。

输出图像

import numpy as np
import matplotlib.pyplot as plt

'''这里使用NumPy的linspace函数在0到10之间生成了200个等间距的数字，
并将其转换为PyTorch张量，方便后续计算。'''
x = np.linspace(0, 10, 200)
x_t = torch.Tensor(x).view((200, 1))

y_t = model(x_t)

'''这里使用PyTorch张量的data属性将其转换为NumPy数组，
并使用matplotlib库的plot函数绘制出曲线。'''
y = y_t.data.numpy()
plt.plot(x, y)

plt.plot([0, 10], [0.5, 0.5], c='r') # 这里绘制了红色的水平分界线，表示y值为0.5时的x轴取值范围
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()

完整代码

x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])
#-------------------------------------------------------#
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, x):
y_pred = F.sigmoid(self.linear(x))
return y_pred
model = LogisticRegressionModel()
#-------------------------------------------------------#
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
#-------------------------------------------------------#
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()

使用逻辑斯蒂回归处理二分类问题的整个过程：

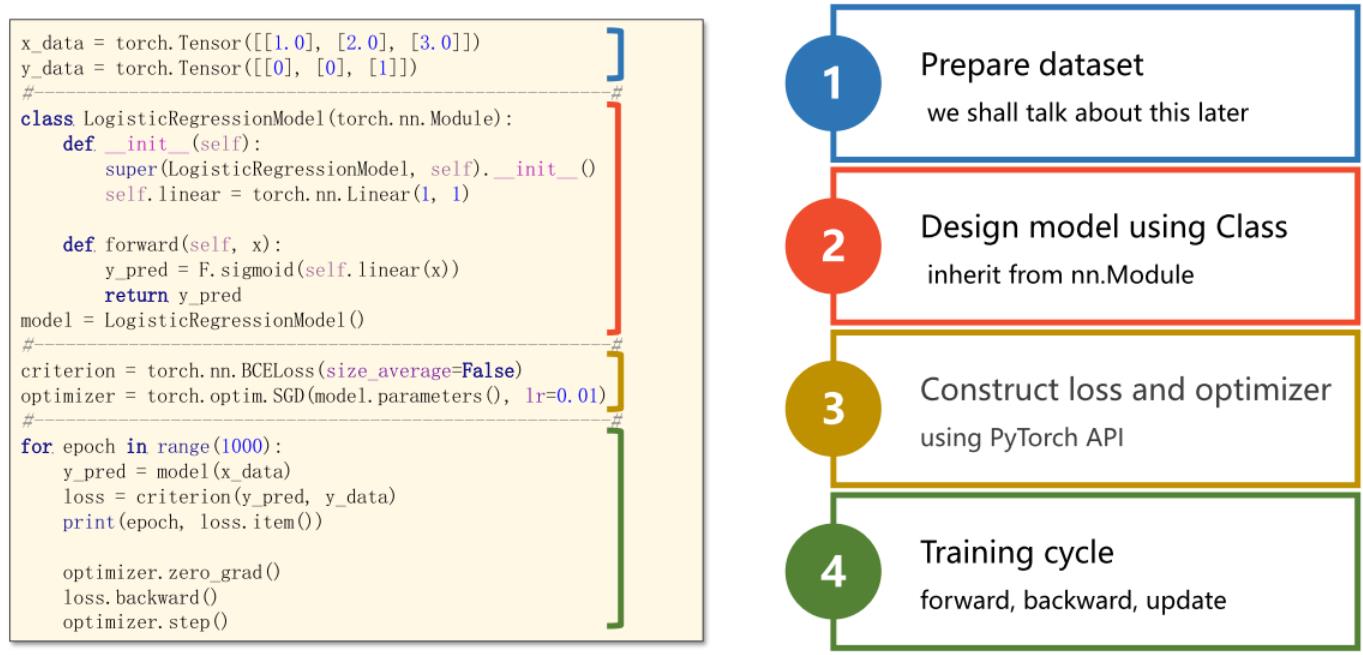
官方文档链接：https://pytorch.org/docs/stable/nn.html?highlight=bceloss#torch.nn.BCELoss

以上是关于Lecture6 逻辑斯蒂回归(Logistic Regression)的主要内容，如果未能解决你的问题，请参考以下文章

logistic regression与最大熵模型·逻辑斯蒂回归模型

Logistic Regression逻辑斯蒂回归

用二项逻辑斯蒂回归解决二分类问题

逻辑斯蒂回归（Logistic Regression）

pytorch学习笔记：逻辑斯蒂回归（Logistic Regression）

梯度下降法解逻辑斯蒂回归