蒙特卡洛计算圆周率

Posted 2023-03-03 科研路上的小C

使用MC计算圆周率的小例子，使用python的numpy，matplotlib库

import numpy as np

import matplotlib.pyplot as plt

def mc_calculate_pi(t):

np.random.seed(t)

rand_num = np.random.rand(t)

rand_num2 = np.random.rand(t)

l1 = rand_num-0.5

l2 = rand_num2-0.5

l0 = np.array([0,0])

list_c =[]

list_d =[]

num1 = 0

num2 =0

for i in range(t):

x,y= l1[i],l2[i]

d = np.array([x,y])

#d=np.array([3,4])

dist = np.sqrt(np.sum(np.square(d- l0)))

if dist<0.5:

list_c.append(d)

num1 = num1+1

else:

list_d.append(d)

num2 = num2+1

pi = 4*num1/(num1+num2)

p = ((pi-3.1415926)/3.1415926)*100

list_c1 = np.array(list_c)

list_d1 = np.array(list_d)

print(num1,num2,pi,np.around(np.absolute(p),2))

plt.figure( figsize=(5,5) )

plt.xlim(-0.5,0.5)

plt.ylim(-0.5,0.5)

plt.scatter(list_c1[:,0],list_c1[:,1],c ="red",s = 0.1)

plt.scatter(list_d1[:,0],list_d1[:,1],s = 0.1)

plt.show()

t= [100,1000,10000,100000,1000000,10000000]

for i in t:

print("n=",i)

mc_calculate_pi(i)

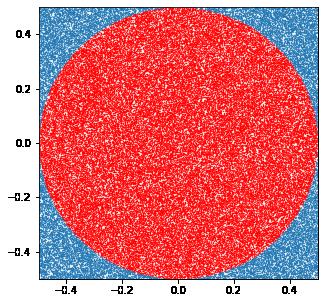
采样10万次的结果：

π= 3.14608，误差0.14%