参加CUDA线上训练营CUDA进阶之路 - Chapter 7 -原子操作

Posted 2023-03-03 Chiao.

7.1 原子操作的基本概念

CUDA的原子操作可以理解为对一个Global Memory或Shared Memory中变量进行“读取-修改-写入”这三个操作为一个最小单位的执行过程。它在执行过程中不允许其他并行线程对该变量进行读取和写入操作。

CUDA中的原子操作本质上是让线程在某个内存单元完成读-修改-写的过程中不被其他线程打扰。基于这个机制，原子操作实现了对在多个进程间共享的变量的互斥保护，确保任何一次对变量的操作的结果的确定性。

没有原子操作的后果

Kernel程序最后面直接写 $x=x+a$。执行到这一步时, 有很多线程想读取x的值，同时也有很多线程想写入x的值，这就会产生不确定性的错误。

7.1.1 向量元素求和

难点是如何利用shared memory实现分而治之，并且合理地安排线程。最需要注意的地方在于并不是所有线程在所有步骤都会有动作。这里先介绍一种避免使用原子操作的方法。

假设有一个大小为2048的向量，我们想用归约算法对该向量求和。于是我们申请了一个大小为1024的线程块，并声明了一个大小为2048的共享内存数组，并将数据从全局内存拷贝到了该共享内存数组。

我们可以有以下两种方式实现归约算法：

不连续的约归

如下图所示，同一个Block内的相邻线程在共享内存中的访问步长为2，因此是不连续的约归方式，而由之前的文章访问步长与bank conflict一节节所讲，这将会发生Bank Conflict。

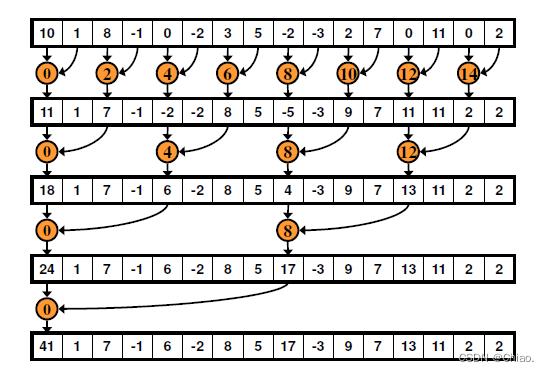
实现代码如下：

// 非连续的归约求和
__global__ void BC_addKernel(const int *a, int *r)

    __shared__ int cache[ThreadsPerBlock];
    int tid = blockIdx.x * blockDim.x + threadIdx.x;
    int cacheIndex = threadIdx.x;

    // copy data to shared memory from global memory
    cache[cacheIndex] = a[tid];
    __syncthreads();

    // add these data using reduce
    for (int i = 1; i < blockDim.x; i *= 2)
    
        int index = 2 * i * cacheIndex;
        if (index < blockDim.x)
        
            cache[index] += cache[index + i];
        
        __syncthreads();
    

    // copy the result of reduce to global memory
    if (cacheIndex == 0)
        r[blockIdx.x] = cache[cacheIndex];

连续的约归

如下图所示，同一个Block内的相邻线程在共享内存中的访问步长为1，由于每个线程的ID与操作的数据编号一一对应，因此很明显不会产生bank冲突。

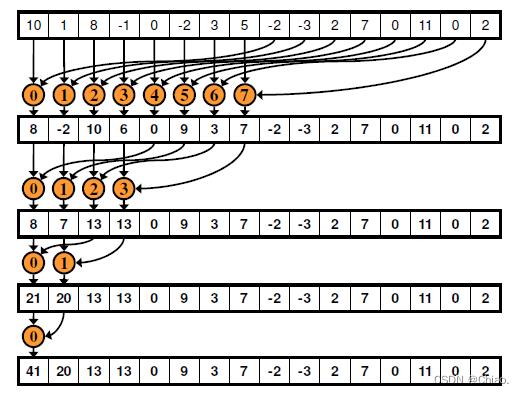
实现代码如下：

// 连续的归约求和
__global__ void NBC_addKernel2(const int *a, int *r)

    __shared__ int cache[ThreadsPerBlock];
    int tid = blockIdx.x * blockDim.x + threadIdx.x;
    int cacheIndex = threadIdx.x;

    // copy data to shared memory from global memory
    cache[cacheIndex] = a[tid];
    __syncthreads();

    // add these data using reduce
    for (int i = blockDim.x / 2; i > 0; i /= 2)
    
        if (cacheIndex < i)
        
            cache[cacheIndex] += cache[cacheIndex + i];
        
        __syncthreads();
    

    // copy the result of reduce to global memory
    if (cacheIndex == 0)
        r[blockIdx.x] = cache[cacheIndex];

代码的过程如下图所示，注意这样则到的结果仍然是一个数组，数组中的一个数代表一个Block所对应数据之和。也就是说，上述过程仅能算出一个Block内的数据之和。要进一步获得向量所有元素之和，则将上一步的输出结果作为第二次核函数执行的输入即可。

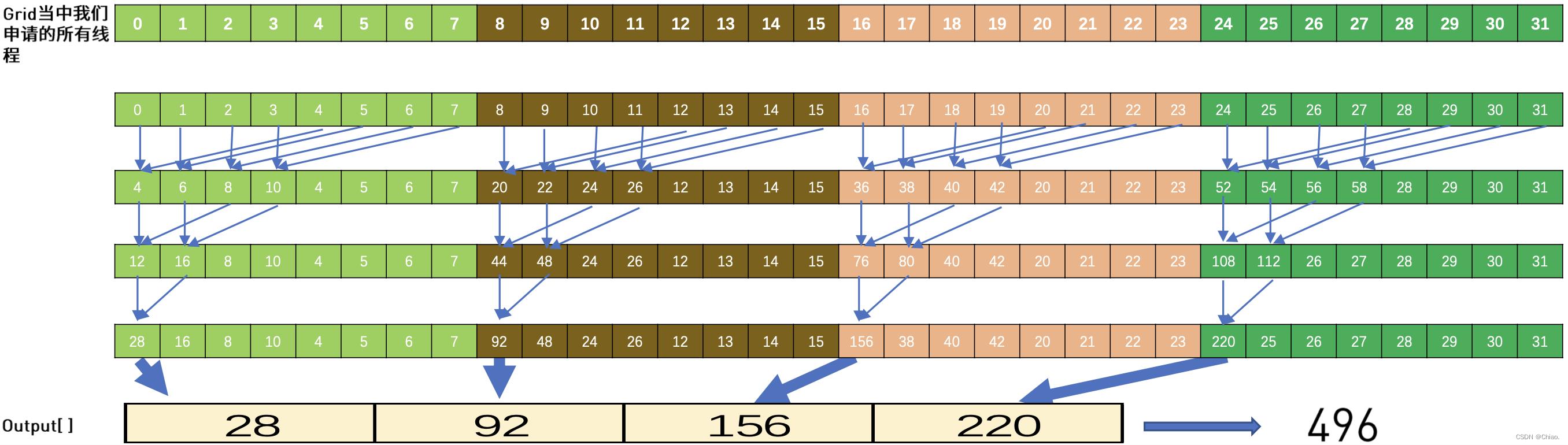
由此可见，对向量进行求和，如果不用原子操作，则还需要将核函数执行多次才能得到最终的结果。

7.2 原子操作的常用函数

原子函数对驻留在全局或共享内存中的一个32位或64位字执行读-修改-写原子操作。

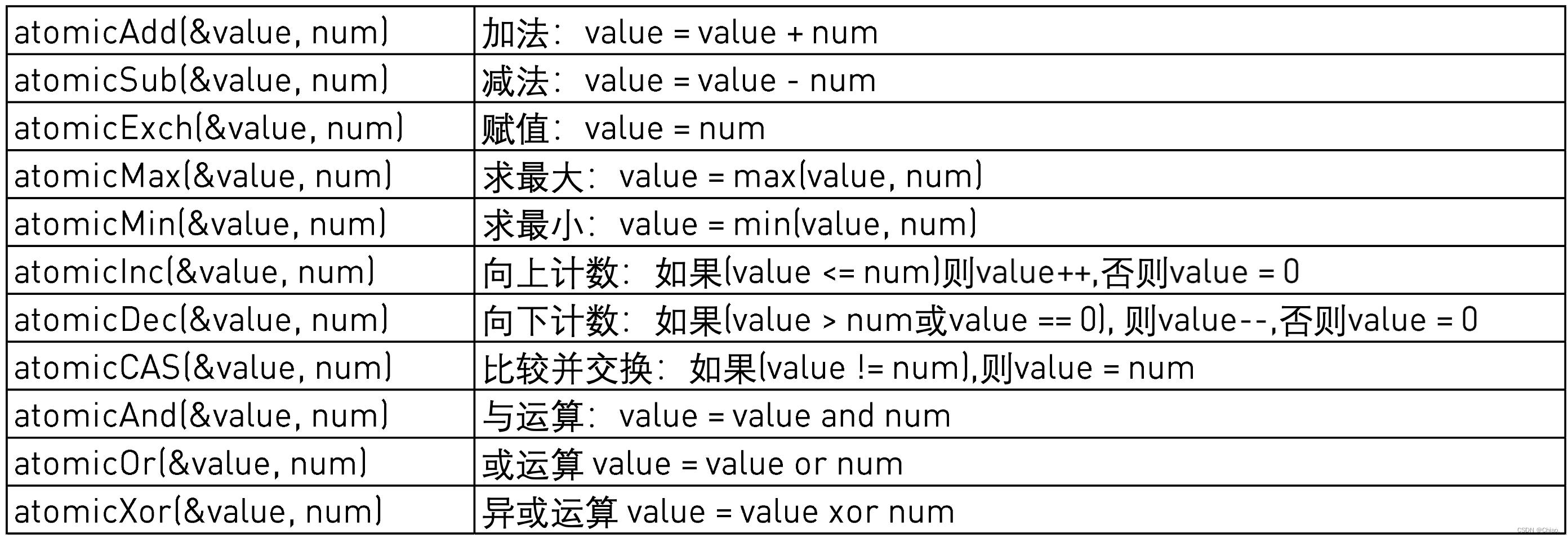
7.3 原子操作向量求和实例

前面提到过，在不使用原子操作的情况下，无法对存储单元中的任何一个变量进行累加操作，因为有很多线程想读取x的值的同时，也有很多线程想写入x的值，这样会产生不确定性的错误。

而引入原子操作就可以让各个线程之间彼此互不影响，可将结果累加到output，就不需要再在第二轮的执行了。

实现代码如下：

__global__ void _sum_gpu(int *ptr, int count, int *result)
    __shared__ int sum_per_block[THREADSPERBLOCK];

    int tmp = 0;
    for(int idx = threadIdx.x + blockIdx.x * blockDim.x; idx < count; idx += gridDim.x * blockDim.x)
        tmp += ptr[idx];
    

    sum_per_block[threadIdx.x] = tmp;
    __syncthreads();

    for(int length = THREADSPERBLOCK / 2; length > 0; length /= 2)
        int sum_up = -1;
        if(threadIdx.x < length)
            sum_up = sum_per_block[threadIdx.x] + sum_per_block[threadIdx.x + length];
//            __syncthreads();
            sum_per_block[threadIdx.x] = sum_up;
            __syncthreads();
        
    

    if(threadIdx.x == 0) 
        |\\colorboxOrangeRed!40atomicAdd(result, sum\\_per\\_block[0])|;