回归问题与神经元模型（DL笔记整理系列）

Posted 2023-02-26 繁凡さん

《繁凡的深度学习笔记》第 2 章 回归问题与神经元模型（DL笔记整理系列）

[e-mail]

https://fanfansann.blog.csdn.net/

https://github.com/fanfansann/fanfan-deep-learning-note

作者：繁凡

version 1.0  2022-1-20

 

声明：

1）《繁凡的深度学习笔记》是我自学完成深度学习相关的教材、课程、论文、项目实战等内容之后，自我总结整理创作的学习笔记。写文章就图一乐，大家能看得开心，能学到些许知识，对我而言就已经足够了 ^q^ 。

2）因个人时间、能力和水平有限，本文并非由我个人完全原创，文章部分内容整理自互联网上的各种资源，引用内容标注在每章末的参考资料之中。

3）本文仅供学术交流，非商用。所以每一部分具体的参考资料并没有详细对应。如果某部分不小心侵犯了大家的利益，还望海涵，并联系博主删除，非常感谢各位为知识传播做出的贡献！

4）本人才疏学浅，整理总结的时候难免出错，还望各位前辈不吝指正，谢谢。

5）本文由我个人（ CSDN 博主 「繁凡さん」（博客） ， 知乎答主 「繁凡」（专栏）， Github 「fanfansann」（全部源码） ， 微信公众号 「繁凡的小岛来信」（文章 P D F 下载））整理创作而成，且仅发布于这四个平台，仅做交流学习使用，无任何商业用途。

6）「我希望能够创作出一本清晰易懂、可爱有趣、内容详实的深度学习笔记，而不仅仅只是知识的简单堆砌。」

7）本文《繁凡的深度学习笔记》全汇总链接：《繁凡的深度学习笔记》前言、目录大纲 https://fanfansann.blog.csdn.net/article/details/121702108

8）本文的Github 地址：https://github.com/fanfansann/fanfan-deep-learning-note/ 孩子的第一个 『Github』！给我个 $\boxed{⭐\text{Starred}}$ 嘛！谢谢！！o(〃＾▽＾〃)o

9）此属 version 1.0 ，若有错误，还需继续修正与增删，还望大家多多指点。本文会随着我的深入学习不断地进行完善更新，Github 中的 P D F 版也会尽量每月进行一次更新，所以建议点赞收藏分享加关注，以便经常过来回看！

如果觉得还不错或者能对你有一点点帮助的话，请帮我给本篇文章点个赞，你的支持是我创作的最大动力！^0^

如果没人点赞的话自然就更新慢咯 >_<

本章目录

• 《繁凡的深度学习笔记》第 2 章 回归问题与神经元模型
• • 2.1 线性回归
  • • 2.1.1 线性模型
  • 2.2 神经元模型
  • • 2.2.1 神经元
    • 2.2.2 优化方法
    • • 2.2.2.1 梯度下降算法
      • • 2.2.2.1.1 Jacobian 和 Hessian 矩阵（选学）
        • 2.2.2.1.2 有限差分法与对称导数法估计梯度大小（选学）
      • 2.2.2.2 最小二乘法
    • 2.2.3 神经元线性模型实战
  • 2.3 再探回归
  • • 2.3.1 非线性模型
  • 2.4 面试题目集锦
  • 2.5 参考资料

本章话题（点击即可跳转哟）：

话题 1 ：什么是回归分析？什么又是回归问题？

话题 2 ：有哪些回归分析方法？

话题 3 ：如何将线性回归模型模型化？

话题 4 ：什么是神经元与神经元模型？

话题 5 ：什么是损失函数？为什么需要使用损失函数？

话题 6 ：回归问题中常用的损失函数有哪些？

话题 7 ：深度学习为什么需要使用优化算法

话题 8 ：有哪些常用的优化算法？

话题 9 ：什么是梯度下降算法？

话题 10 ：梯度下降算法为什么可以优化目标函数？（选学）

话题 11 ：训练过程中如何避免陷入局部最优解？如何逃离鞍点？

话题 12 ： 趣味话题：有时候我们没办法直接计算梯度，可以尝试估计梯度大小吗？- 有限差分法与对称导数法（选学）

话题 13 ：什么是最小二乘法？如何使用最小二乘法解决线性回归问题？

话题 14 ：道理我都懂，怎么用代码实现并解决神经元线性模型呢？

话题 15 ：线性模型已经完全学会了！如果换成非线性的模型该怎么办呢？

《繁凡的深度学习笔记》第 2 章 回归问题与神经元模型

话题 1 ：什么是回归分析？什么又是回归问题？

  回归分析（Regression Analysis）是一种统计学上分析数据的方法，目的在于了解两个或多个变量间是否相关、相关方向与强度，并建立数学模型以便观察特定变量来 预测 （prediction）研究者感兴趣的变量。在自然科学和社会科学领域，回归经常用来表示 输入和输出之间的关系 。

  在机器学习领域中的大多数任务通常都与 预测 有关。 当我们进行回归分析，想要预测一个预测值在连续的实数范围内时，我们称之为 回归问题 。常见的例子有：预测房价 / 股票、预测需求 / 销量等。但不是所有的 预测 都是回归问题。在下一章节中，我们将介绍 分类问题 。分类问题的目标是预测数据属于一组类别中的哪一种，也即预测一个预测值属于某一段连续的实数区间的方法。

话题 2 ：有哪些回归分析方法？

  统计学中的回归分析方法一般有 线性回归（简单线性回归、复回归、对数线性回归）、非线性回归、对数几率回归、偏回归、自回归（自回归滑动平均模型、差分自回归滑动平均模型、向量自回归模型）。本章主要探讨线性回归与非线性回归，对于其他更多的回归方法仅给出一些简单的介绍，更多详细讲解、代码实现及其应用，详见《繁凡的机器学习笔记》。

$❑$线性回归

  在回归问题中，如果使用线性模型去逼近真实模型，那么我们把这一类方法叫做线性回归（Linear Regression），线性回归是回归问题中的一种具体的实现。

  线性回归基于几个简单的假设：首先，假设自变量 $\mathbf{x}$ 和因变量 $y$ 之间的关系是线性的，即 $y$ 可以表示为 $\mathbf{x}$ 中元素的加权和，这里通常允许包含观测值的一些噪声；其次，我们假设任何噪声都比较正常，如噪声遵循正态分布 （NormalDistribution） $\mathcal{N}\left(\mu ,{\sigma }^2\right)$。

  简单线性回归（simple linear regression），在统计学中指只有一个解释变量的线性回归模型。往往是以单一变量预测，用于判断两变量之间相关的方向和程度。

  复回归分析（multiple regression analysis），也称多变量回归，是简单线性回归的一种延伸应用，用以了解一个因变量与两组以上自变量的函数关系。

  对数线性回归（Log-linear model），是将自变量和因变量都取对数值之后再进行线性回归，所以根据自变量的数量，可以是对数简单线性回归，也可以是对数复回归。

$❑$非线性回归

  非线性回归（non-linear regression），是回归函数关于未知回归系数具有非线性结构的回归。

$❑$对数几率回归

  对数几率回归（Logistic Regression），又称逻辑回归，是一种对数几率模型（英语：Logit model，又译作逻辑模型、评定模型、分类评定模型）是离散选择法模型之一，属于多重变量分析范畴，是社会学、生物统计学、临床、数量心理学、计量经济学、市场营销等统计实证分析的常用方法。关于对数几率回归的更多讲解，详见 《繁凡的深度学习笔记》 第 3 章 分类问题与信息论基础 3.2 逻辑回归。

$❑$自回归模型

自回归模型（Autoregressive model），简称AR模型，是统计上一种处理时间序列的方法，用同一变数例如 $x$ 的之前各时期，也即 $x_1$ 至 $x_{t-1}$ 来预测本期 $x_t$ 的表现，并假设它们为一线性关系。因为这是从回归分析中的线性回归发展而来，只是不用 $x$ 预测 $y$ ，而是用 $x$ 预测 $x$ （自己)；所以叫做自回归。

2.1 线性回归

  我们在 话题 2 中已经讲解过了什么是线性回归，我们继续深入探讨，考虑如何解决线性回归问题。

2.1.1 线性模型

话题 3 ：如何将线性回归模型模型化？

  考虑一个实例：作为一个有志青年，我们想要预测未来的城市房价！我们希望可以根据房屋的面积和房龄来估算房屋的价格。为了开发一个能预测房价的模型，我们首先需要收集一个真实的数据集。这个数据集包括了房屋的销售价格、面积和房龄。在机器学习的术语中，通常将数据集称之为 训练数据集（training data set）或 训练集（training set）。其中数据集内的每行数据（这里就是与一次房屋交易相对应的各种数据）称为样本（sample），或 数据点（data point）或 数据样本（data instance）。将我们想要预测的目标（这里显然是房屋的价格）称之为标签（label）或目标（target）。预测所依据的自变量（面积和房龄）称为特征（feature）或协变量（covariate）。

  通常，我们使用 $n$ 或者 $m$ 来表示数据集中的样本数。对索引为 $i$ 的样本，其输入表示为 ${\mathbf{x}}^{(i)}=[x_1^{(i)},x_2^{(i)}{]}^{\mathrm{T}}$ ，其对应的标签是 $y^{(i)}$ 。

  这里线性回归的线性假设指目标（房屋价格）可以表示为特征（面积和房龄）的加权和，如下面的式子：
$$\mathrm{price}=w_{\mathrm{area}}\cdot \mathrm{area}+w_{\mathrm{age}}\cdot \mathrm{age}+b.\text{\hspace{1em}(2.1)}$$

式中的 $w_{\mathrm{area}}$​​ 和 $w_{\mathrm{age}}$​​ 称为权重（weight）， $b$​​ 称为偏置（bias），或称为偏移量（offset）、截距（intercept）。

  权重决定了每个特征对我们预测值的影响。偏置是指当所有特征都取值为 $0$ 时，预测值应该为多少。如果没有偏置项，我们模型的表达能力将受到限制。 严格来说，上式是输入特征的一个仿射变换（affine transformation）。仿射变换的特点是通过加权和对特征进行线性变换（linear transformation），并通过偏置项来进行平移（translation）。

  至此问题就变为了：给定一个数据集，我们的目标是寻找模型的权重 $\mathbf{w}$​ 和偏置 $b$​ ，使得根据模型做出的预测大体符合数据里的真实价格。输出的预测值由输入特征通过线性模型的仿射变换决定，仿射变换由所选权重和偏置确定。显然我们只需要求出符合实际情况的模型参数 $\mathbf{w},b$​，就可以得到一个可以大致预测房屋价格的线性模型。这种模型被发现与人类的神经元模型十分吻合，我们考虑从神经元模型的角度出发解决上面的问题。

2.2 神经元模型

2.2.1 神经元

话题 4 ：什么是神经元与神经元模型？

  神经元（Neuron），即神经元细胞（Nerve Cell），是神经系统最基本的结构和功能单位。如图 2.1 所示，典型的生物神经元结构分为细胞体和突起两大部分。成年人大脑中包含了约 1000 亿个神经元，每个神经元通过树突获取输入信号，通过轴突传递输出信号，神经元之间相互连接构成了巨大的神经网络，从而形成了人脑的感知和意识基础。

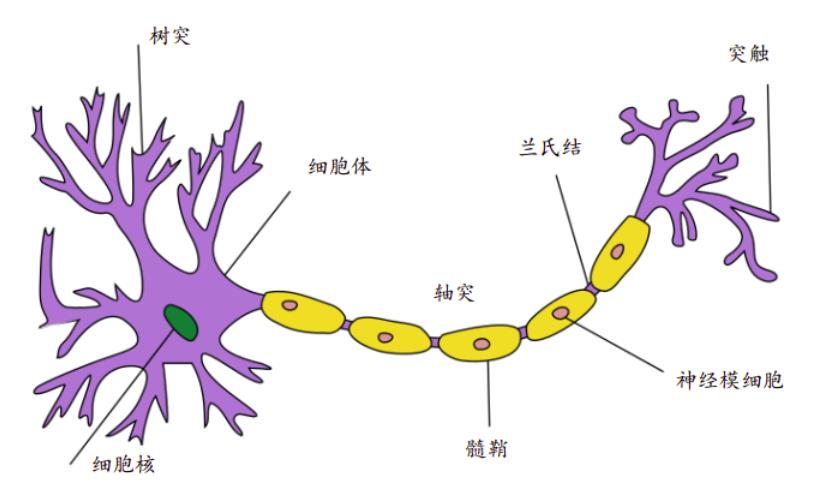
图 2.1 神经元

  

  在神经元中，树突中接收到来自其他神经元或视网膜等环境传感器的信息 $x_i$​​ 。该信息通过突触权重 $w_i$​​ 来加权，以确定输入的影响（即通过设置突触权重的大小，使 $w_i$​​ 与 $x_i$​ 相乘 来 激活 或 抑制该输入信息）。 来自多个源的加权输入以加权和 $y=\sum _i{x}_i{w}_i+b$​​ 的形式汇聚在细胞核中，然后将这些信息发送到轴突 $y$​​ 中进一步处理，通常会通过 $\sigma (y)$​​ 进行一些非线性处理。之后，它要么到达目的地（例如肌肉），要么通过树突进入另一个神经元（一层又一层地组成神经网络）。

  考虑将生物神经元 (Neuron) 的模型抽象成具体的数学模型得到 神经元模型：对于神经元的输入向量 $\mathbf{x}=[x_1,x_2,x_3,\dots ,x_n{]}^{\mathrm{T}}$，经过函数映射：$f_{\theta }:\mathbf{x}\to y$ 后得到输出 $y$ ，其中 $\theta$ 为函数 $f$ 自身的参数。考虑一种简化的情况，即线性变换，对于两个列向量 $\mathbf{x},\mathbf{w}$，我们希望可以计算得到类似神经元模型 $y=\sum _i{x}_i{w}_i+b$ 的值，我们可以将其中一个列向量转置之后相乘： 𝑓 ( 𝒙 ) = 𝒘 T 𝒙 + 𝑏 𝑓(𝒙) = 𝒘^\\mathrm T 𝒙 + 𝑏 f(x)=w