Java实现数据结构——红黑树
Posted x_k
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Java实现数据结构——红黑树相关的知识,希望对你有一定的参考价值。
红黑树定义
相比二叉查找树,红黑树中的节点多个颜色属性。通过颜色属性,确保了从根节点到每个叶子节点的简单路径,没有一条路径超过其他路径2倍,近似于平衡。
性质:
- 每个节点或是红色,或是黑色
- 根节点是黑色
- 每个叶节点是黑色
- 如果一个节点是红色,那么它的两个子节点都是黑色
- 对于每个节点,从该节点到其所有后代叶节点的简单路径上,包含相同数目的黑色节点
Java代码实现中,性质3:每个叶节点为黑色,默认无值叶节点指向Null
旋转
通过旋转操作,改变树中节点的指针结构,并且保持二叉查找树性质(当前节点大于等于左子树所有节点,小于右子树所有节点)。
左旋
将当前节点移动到其左孩子节点的位置,右孩子移动到当前节点的位置
步骤:
- 关联当前节点c和其右孩子的左孩子
- 关联当前节点的双亲和右孩子
- 关联当前节点和右孩子
/**
* 左旋
*
* @param root 根结点
* @param c 当前结点
* @return 根结点
*/
public <E> RBTreeNode<E> rotateLeft(RBTreeNode<E> root, RBTreeNode<E> c)
RBTreeNode<E> r, cp, rl;
if (c != null && (r = c.right) != null)
// 1.connect c and rl
if ((rl = c.right = r.left) != null)
rl.parent = c;
// 2.connect r and cp
if ((cp = r.parent = c.parent) == null)
(root = r).red = false; // done if c is root
else if (cp.left == c)
cp.left = r;
else
cp.right = r;
// 3.connect c and r
r.left = c;
c.parent = r;
return root;
右旋
将当前节点移动到其右孩子节点的位置,左孩子移动到当前节点的位置
步骤:
- 关联当前节点和其左孩子的右孩子
- 关联当前节点的双亲和其左孩子
- 关联当前节点和其左孩子
/**
* 右旋
*
* @param root 根结点
* @param c 当前结点
* @return root 根结点
*/
public <E> RBTreeNode<E> rotateRight(RBTreeNode<E> root, RBTreeNode<E> c)
RBTreeNode l, cp, lr;
if (c != null && (l = c.left) != null)
// 1.connect c and lr
if ((lr = c.left = l.right) != null)
lr.parent = c;
// 2.connect l and cp
if ((cp = l.parent = c.parent) == null)
(root = l).red = false;
else if (cp.left == c)
cp.left = l;
else
cp.right = l;
// 3.connect c and l
l.right = c;
c.parent = l;
return root;
插入
查找树的插入位置,可参考二叉查找树-添加元素
根据红黑树的基本性质,新增节点的颜色为红色更为方便进行操作(黑色的话会破坏性质5)
在插入节点为红色的前提下,破坏红黑树的性质有且仅有下面两种情况:
- 插入节点为根节点(空树新增节点)
- 插入节点的父节点为红色
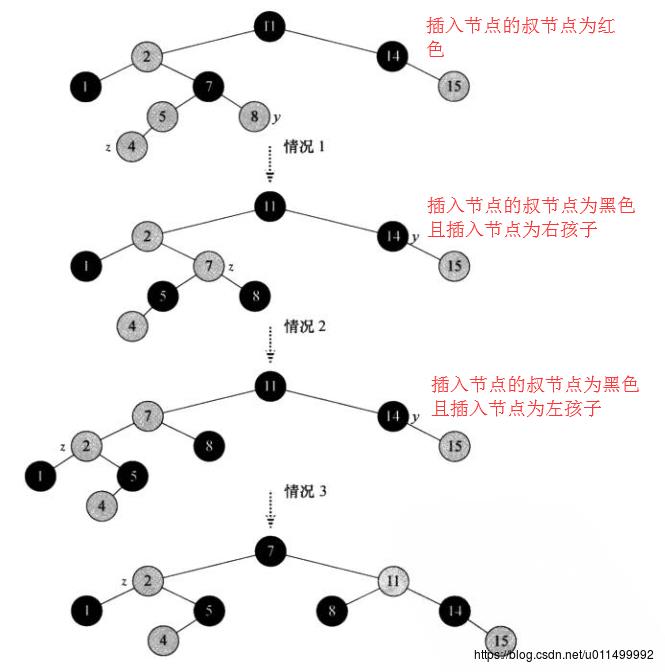
插入节点x的父节点xp是左孩子
迭代下面操作,直到x或xp为根节点:
1. 如果x的叔父节点u为红色:将x的祖父节点xpp的黑色属性赋予给它的两个孩子,xpp设置为x节点。
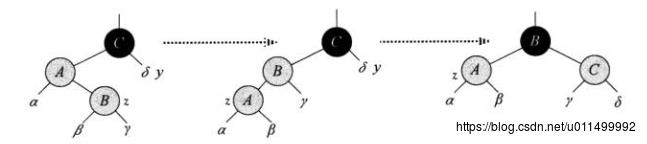
2. 如果x的叔父节点u为黑色,且x为右孩子:以xp左旋(由于x和xp都是红色,不影响黑高),将x设置为xp。此时,x为左孩子。
3. 如果x的叔父节点u为黑色,且x为左孩子:xp和xpp的颜色互换,并且,以xpp做右旋,平衡黑高
算法导论截图:
步骤2和步骤3解决的问题:
插入节点x的父节点xp是右孩子
迭代下面操作,直到x或xp为根节点:
1. 如果x的叔父节点u为红色:将x的祖父节点xpp的黑色属性赋予给它的两个孩子,xpp设置为x节点。
2. 如果x的叔父节点u为黑色,且x为左孩子:以xp右旋(由于x和xp都是红色,不影响黑高),将x设置为xp。此时,x为右孩子。
3. 如果x的叔父节点u为黑色,且x为右孩子:xp和xpp的颜色互换,并且,以xpp做左旋,平衡黑高
Java代码实现
@Override
public boolean insert(E e)
// 1、关联插入位置
RBTreeNode<E> newNode = createRBTreeNode(e);
RBTreeNode<E> parent = null; // 插入元素的父结点
if (root == null)
root = newNode;
root.red = false;
else
RBTreeNode<E> current = root;
while (current != null)
if (e.compareTo(current.e) < 0)
parent = current;
current = current.left;
else if (e.compareTo(current.e) > 0)
parent = current;
current = current.right;
else
return false;
if (e.compareTo(parent.e) < 0)
parent.left = newNode;
else
parent.right = newNode;
newNode.parent = parent;
// 2、保持红黑树性质
root = this.balanceInsertion(root, newNode);
size++;
return true;
/**
* 平衡插入后的树
*
* @param root 根结点
* @param x 插入结点
*/
public <E> RBTreeNode<E> balanceInsertion(RBTreeNode<E> root, RBTreeNode<E> x)
// 1.遍历结点必为红结点
x.red = true;
for (RBTreeNode<E> xp, xpp, xppl, xppr; ; )
// 2-1.空树
if ((xp = x.parent) == null)
x.red = false;
return x;
// 2-2.xp为黑结点 || xp为根结点
else if (!xp.red || (xpp = xp.parent) == null)
return root;
// 2-3-1.xp is left-child
// case1: a -> b
if (xp == (xppl = xpp.left))
// 2-3-1-1.x uncle is red
if ((xppr = xpp.right) != null && xppr.red)
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
// 2-3-1-2.x uncle is black
else
// x is right-child
// case2: b -> c
if (x == xp.right)
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
// x is left-child
// case3: c -> d
if (xp != null)
xp.red = false;
if (xpp != null)
xpp.red = true;
root = rotateRight(root, xpp);
// 2-3-2.xp is right-child
else
// 2-3-2-1.x uncle is red
if ((xppl = xpp.left) != null && xppl.red)
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
// 2-3-2-2.x uncle is black
else
// x is left-child
if (x == xp.left)
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
// x is right-child
if (xp != null)
xp.red = false;
if (xpp != null)
xpp.red = true;
root = rotateLeft(root, xpp);
总结
当插入节点的叔父节点为黑色的时候,x和xp转换为同侧,即:(xpp.left=xp & xp.left=x)或(xpp.right=xp & xp.right = x)
GitHub查看源码
以上是关于Java实现数据结构——红黑树的主要内容,如果未能解决你的问题,请参考以下文章