[CTF从0到1学习] 二CTF 密码学

Posted 2023-02-06 南岸青栀*

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[CTF从0到1学习] 二CTF 密码学相关的知识，希望对你有一定的参考价值。

密码学

文章目录

密码学
编码与密码
CTF Wp

概述

密码学是研究编制密码和破译密码的技术科学
使信息保密的技术和科学学叫密码编码学
破译密文的科学与技术叫密码分析学

信息安全的基本模型

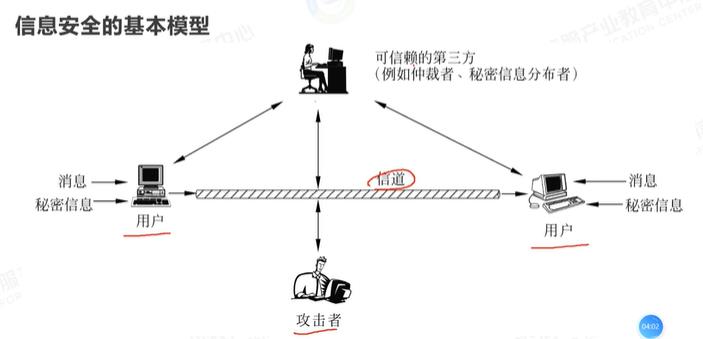
密码学基本概念

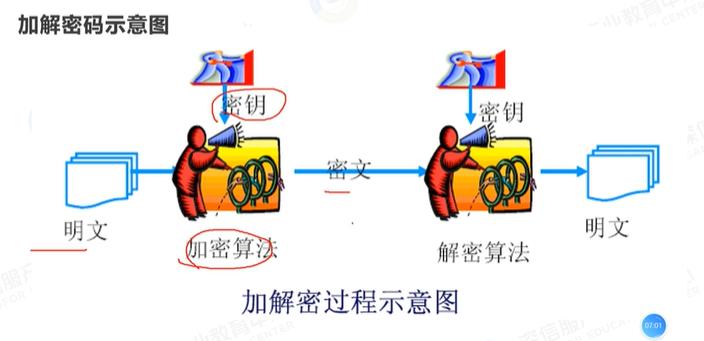
明文：没有加密的文字or字符串
密文：对明文加密之后的报文
加密算法：
解密算法
加密密钥
解密密钥
单钥密码体系
双钥密码体系

密码学的历史与发展

第一阶段（1949年前）古典密码发展阶段

隐写术，暗语，隐语，藏头诗等
采用手工或机械变换的方式实现
单表代换密码：Caesar密码、仿射密码
多表代换密码：Vigenere，Hill密码等
转轮密码：Enigma，Red密码等

第二阶段：近代密码阶段（1949~1976）

1949，Shannon发表了《保密系统的通信理论》，用信息论的观点分析了密码学的基本原理，奠定了密码学的基本理论。
1967年David Kahn出版了《破译者》一书

现代密码学阶段（1976~至今）

1976年，Diffie、Hellman发表了《密码学新方向》，开辟了公钥密码学的新领域
1976年，美国建立了DES为联邦标准

现代密码学的主要发展方向

混沌密码学：混沌加密的基本原理是利用混沌系统产生混沌系列作为密钥序列，接收方用混沌同步的方法将明文信号提取出来实现解密
量子密码学：量子密码学利用量子力学的特性来加密的科学。任何试图尝试读取量子态的行动都会改变量子态本身。

密码体制分类

受限制的（restricted）算法：算法的保密性基于保密算法的秘密。
基于密钥（key-based）的算法：算法的保密性基于对密钥的保密。

一个加密系统S可以用数学符号描述如下：

S=P,C,K,E,D

P --- 明文空间，表示全体可能出现的明文集合
C --- 密文空间，表示全体可能出现的密文集合
K --- 密钥空间，密钥是加密算法中的可变参数
E --- 加密算法，由一些公式，法则或程序构成
D --- 解密算法，E的逆

当给定密钥k时，各符号的关系

C = Ek(P), 对明文P加密后得到密文C
P = Dk(C) = Dk(Ek(P)), 对密文C解密后得明文P
加密设计主要是确定E，D，K

优秀密码算法应该是基于密钥的保密，而非算法的保密

现代密码学用密钥解决问题，密钥用K表示

密钥K的可能值的范围叫做密钥空间（keyspace）

单钥体制，对称加密

流密码

分组密码

双钥体制

1976年，Diffie和Hellman首先引入

一对密钥：公钥和密钥

密码攻击

攻击类型	攻击者掌握的内容
唯密文攻击	加密算法截获的部分密文
已知明文攻击	加密算法截获的部分密文一个或多个明文密文对
选择明文攻击	加密算法截获的部分密文自己选择的明文消息，以及由密钥产生的相对密文
选择密文攻击	加密算法截获的部分密文自己选择的密文消息，以及相应的被解密的明文

算法的安全性

如果破译算法的代价大于加密数据价值，那么加密算法是安全的

如果破译算法所需要的时间比加密数据保密的时间长，那么你可能是安全的

编码与密码

编码基础

ASCII

标准ASCII码，使用 7 位二进制数（剩下的一位二进制为0）来表示所有的大小写字母，数字，标点符号。

后128个称为扩展ASCII码，许多基于x86的系统都支持使用扩展ASCII。扩展ASCII码允许将每个字符的第八位用于确定附加的128个特殊符号字符，外来语字母和图形符号

扩展ASCII表

unicode

因为ASCII只有8位，只能表达256种字符。所以出现unicode，unicode是国际组织制定的可以容纳世界上所有文字和符号的字符编码方案。使用16位的编码空间（每个字符占用2个字节）

UTF-8（8-bit Unicode Transformation Format）是一种针对Unicode 的可变长度字符编码。

UTF-8使用1~6个字节为每个字符编码

BASE64

Base64是一种基于64个可打印字符来表示二进制数据的表示方法。

每6个比特位一个单元，对应某个可打印字符除了A-Z，a-z，0-9共62个字符还有“+”，“/”，最后用“=”填充不能被3整除的空位。

古典密码学

古典密码的加密是将明文的每一个字母代换为字母表中的另一个字母。

单表代换密码

凯撒密码

凯撒密码加密时将明文中的每个字母按字母表顺序向前或向后移动固定数目作为密文

移位密码

与凯撒密码类似，最早的凯撒密码是固定左移3位。

移位密码可以任意移动，后期不仅处理26个字母，还会处理数字和特殊字符。参照ASCII表进行位移

仿射密码

例子：

加密

解密：

多表代换密码

查找矩阵替换：

若两个字母同行，则用右方字母替换

若两个字母同列，则用下方字母替换

若既不同行也不同列，则用矩阵对角字母替换

polybius密码（棋盘密码）

vigenere密码

使用26个字母构成字母矩阵横行为明文列，纵向为密钥列

其他类型密码

培根密码

二进制思想：粗体字为B，正常字为A

栅栏密码

将明文分成N个一组，然后每组的第一个连起来

摩斯密码

用.和_表示，以前用于发电报

CTF中奇怪密码

倒序加密

电脑键盘密码

键盘密码

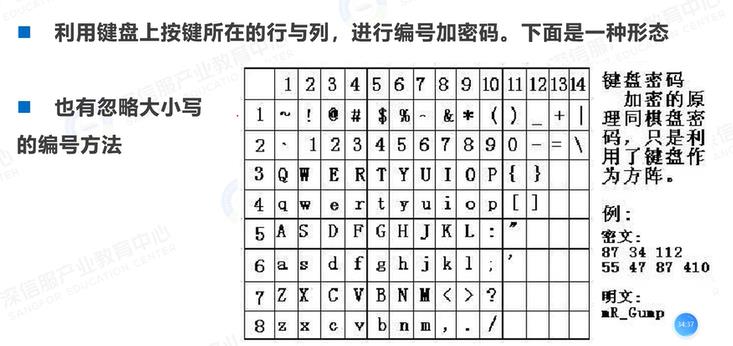
手机键盘加密

当铺密码

用汉子来表示数字，进行编码。汉子特点是出头数量

猪圈密码

对称加密

基本概念

特征：加密解密使用相同的密钥（单密钥加密）

根据加密对象分为

流加密：每次加密都通过密钥生成一个密钥流，解密也是使用同一个密钥流，明文与同样长度的密钥流进行异或运算得到密文，密文与同样的密钥流进行异或运算得到明文。典型算法RC4。
- RC4：

RC4是典型的流加密算法，常用于SSL/TSL，及802.11和WAP中。

流加密会逐字节加密数据，RC4本质是以密钥为种子产生的随机数来对明文进行逐字节异或。

分组密码与流密码的区别就在于有无记忆性

加密过程

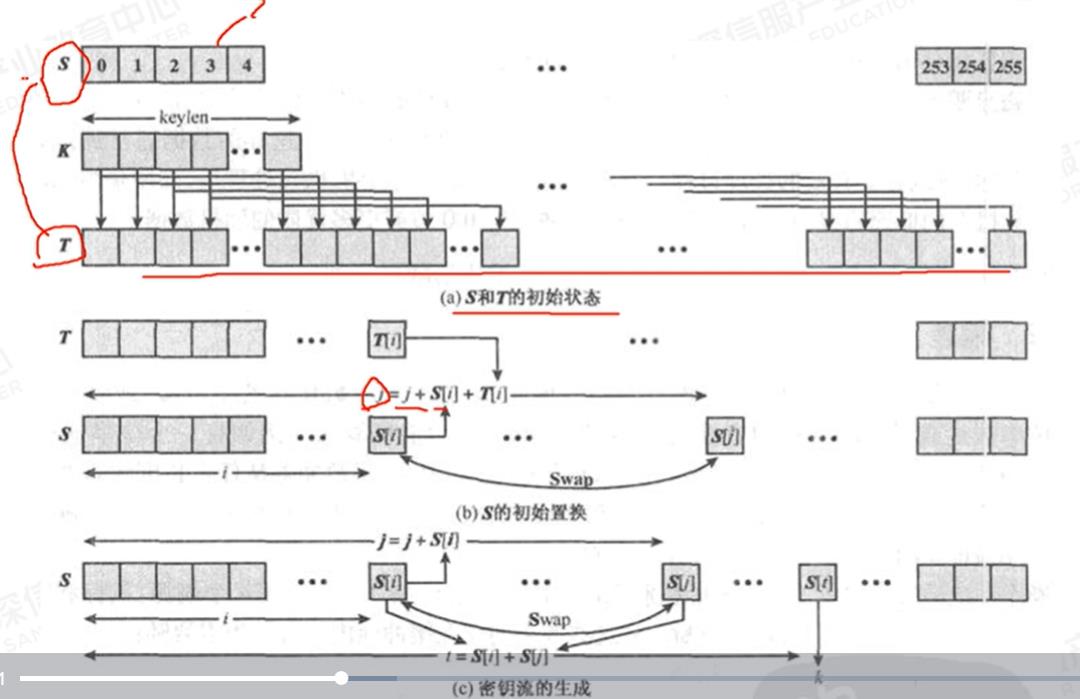
1.初始化S表

（1）对S表进行线性填充，一般为256个字节

（2）用种子密钥填充另一个256字节的K表

（3）用K表对S表进行初始置换

2.密钥流的生成（为每一个待加密的字节生成一个伪随机数，用来异或，S表一旦完成初始化，种子密钥就不再被使用）。

RC4加密实现

# RC4加密算法实现


# 初始化S表
def ini_S(K):
    S = [a for a in range(256)]
    j = 0
    for i in range(256):
        j = (j + S[i] + K[i]) % 256
        S[i],S[j] = S[j],S[i]

    return S

# 种子密码生成临时表
def create_R(seeds):
    T = bytes(seeds, encoding='utf-8')  # 将utf-8的字节码解码成Python默认的unicode的字符串
    T = list(T)  # 转换成列表类型
    print('private seeds:', T)  # 输出密钥
    len_key = len(T)  # 确定密钥的长度
    R = [T[i % len_key] for i in range(256)]  # 对T进行复制和填充，并保存在R数组中

    return R

# 密钥流的生成
def steam_K(S,length):
    i = 0
    j = 0
    Sh = []  # Sh保存流
    length = int(length)  # 保存明文的长度或者密文长度的一半
    for i in range(length):
        i = (i + 1) % 256  # 如果用完256个位置，再从S[i]开始
        j = (j + S[i]) % 256  # 选择S[i]与S的另一个字节
        # 对S[i]和s的另一字节进行交换
        temp = S[i]
        S[j] = S[j]
        S[i] = temp
        h = (S[j] + S[i]) % 256  # 防溢出操作
        k = S[h]
        Sh.append(k)  # 将k在Sh的末尾添加新的对象
    return Sh

if __name__ == '__main__':
    choose = input('choose 1--encryption, 2--decryption:')  # 1为加密，2为解密

    if choose == '1':
        key = input("input the key:")
        R = create_R(key)
        S = ini_S(R)
        plaintext = input("input the plaintext:")
        K = steam_K(S,len(plaintext))
        ciphertext = ''
        for i in range(len(plaintext)):
            ciphertext = ciphertext + '%02x' % (K[i] ^ ord(plaintext[i]))  # 进行异或运算并保存在ciphertext
        print('ciphertext:', ciphertext)  # 输出密文

# 解密操作
    if choose == '2':
        key = input('input the key:')  # key保存密钥
        K = create_R(key)  # K保存key的辅助表
        S = ini_S(K)  # S的初始化
        ciphertext = input('input the ciphertext:')  # ciphertext保存密文
        plaintext = ''  # plaintext保存明文
        Sh = steam_K(S, len(ciphertext)/2)  # 生成密文的流
        # Sh与密文的下一个字节进行异或运算
        for i in range(int(len(ciphertext)/2)):
            plaintext = plaintext + chr(int(ciphertext[0:2], 16) ^ Sh[i])  # 进行异或运算并保存在plaintext
            ciphertext = ciphertext[2:]
        print('plaintext:', plaintext)  # 输出密文

块加密（分组密码），加密和解密序列分为一个个分组，最后吧每一块序列合并到一起，形成明文或密文。根据不同的分组加密方式，每个分组之间可以有联系，也可以没有联系。典型算法DES和AES

DES（data encryption standard，数据加密标准）

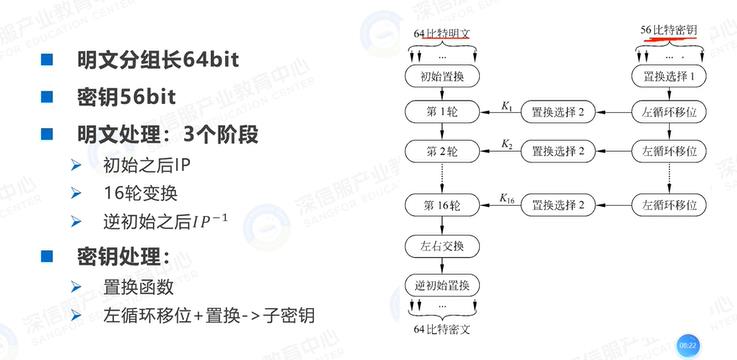
初始置换

轮变换

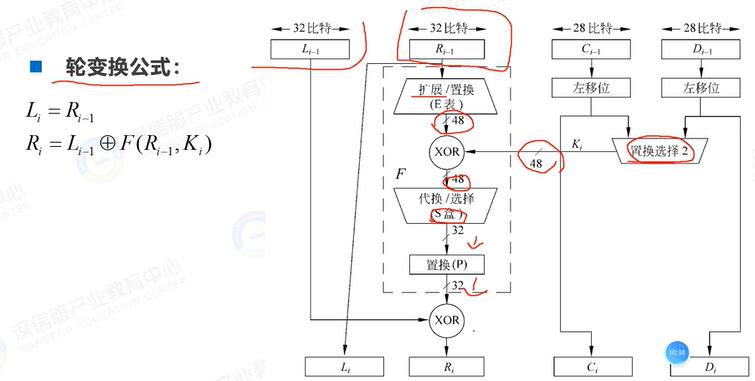
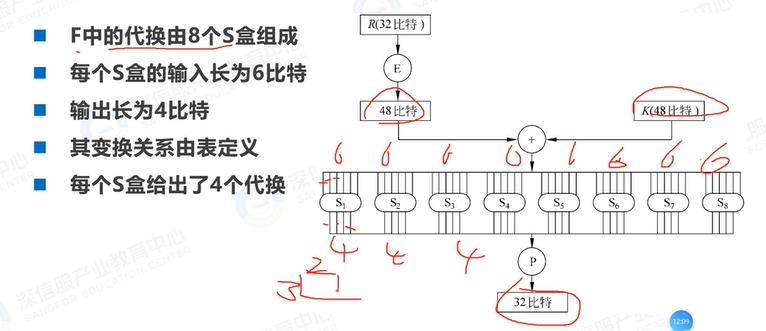
S盒

加密模式

ECB（Electronic CodeBook）

是块加密中比较简单的加密模式。在ECB模式中，每一块明文数据都给独立的进行加密来生成加密块。这意味着如果你发现两个加密块有相同的内容，那么也就可以确定两个加密块的原文是相同的。

CBC（cipher-Block Chaining）

最常见的块加密模式。在CBC中，每个明文块都会自加密前被使用前一个明文快的密文进行异或；解密过程正好相反。其中第一块明文块会被使用IV及初始化向量进行异或。

密码分析

差分密码分析是现在攻击迭代密码最有效的方法之一，基本思想是：通过分析明文对的差值对密文对的差值的影响来恢复某些密钥比特。
线性密码分析是对迭代密码的一种已知明文攻击，利用的是密码算法中的“不平衡（有效）的线性逼近”。

AES（advanced encryotion standard）

公钥密码学

公钥密码体质算法条件

产生一对密钥是计算可行的

已知公钥、明文，产生密文是计算可行的

利用私钥、密文，得到明文是计算可行的

利用公钥来推断私钥是计算不可行的

利用公钥、密文，得到明文是计算不可行的

RSA算法

CTF Wp

给的东西和题目不一样，但是没关系，因为前面几个题都是非常常规的编码方式

编码解码

1.AAencode

发现是一堆颜文字，AAencode主要是将js代码转换为网络表情。我们将密文直接放入浏览器控制台

2.brainfuck

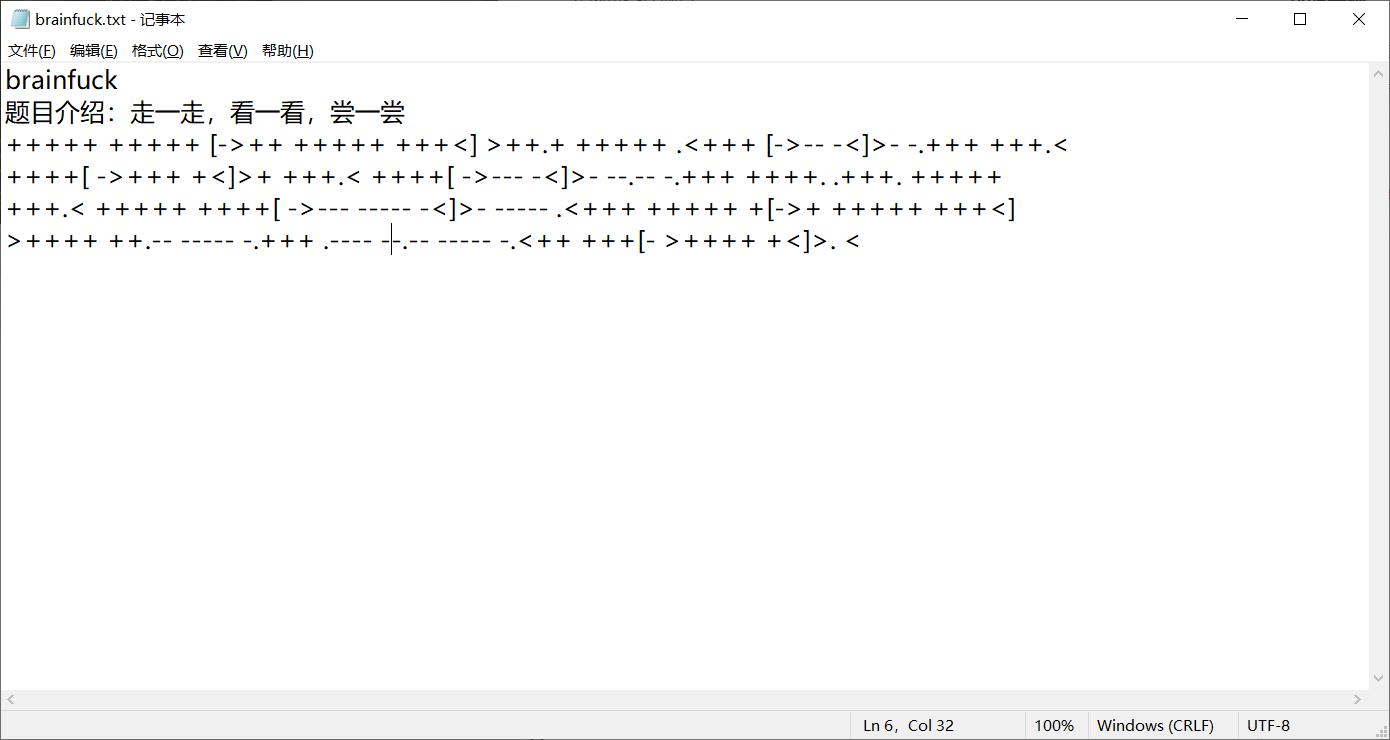
题目提示brainfuck编码，百度一大堆

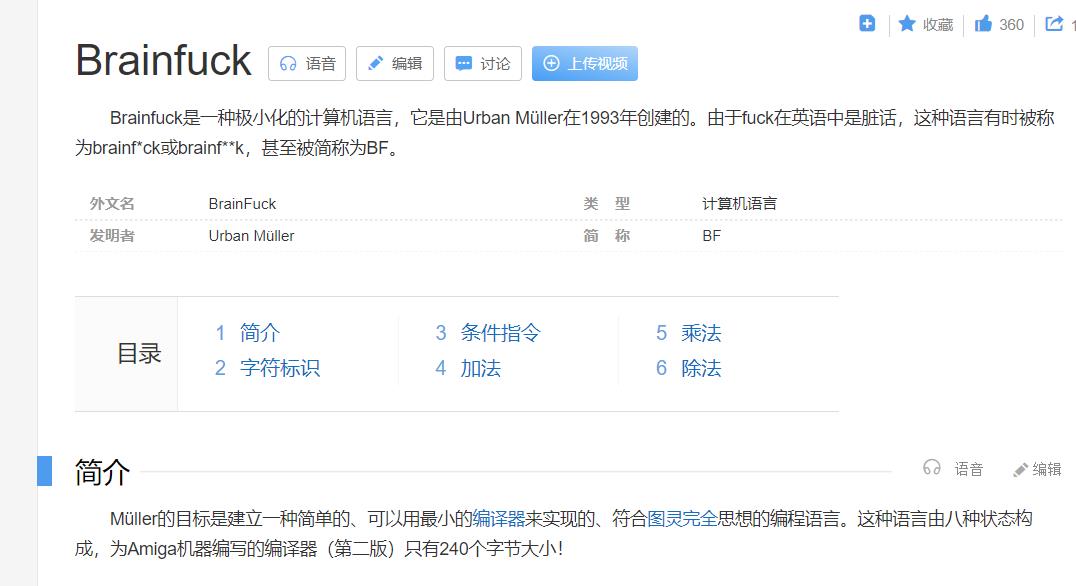
在线编解码网站：https://www.splitbrain.org/services/ook

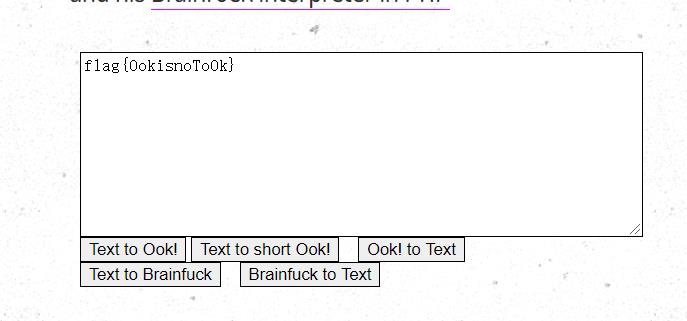
3.Ook

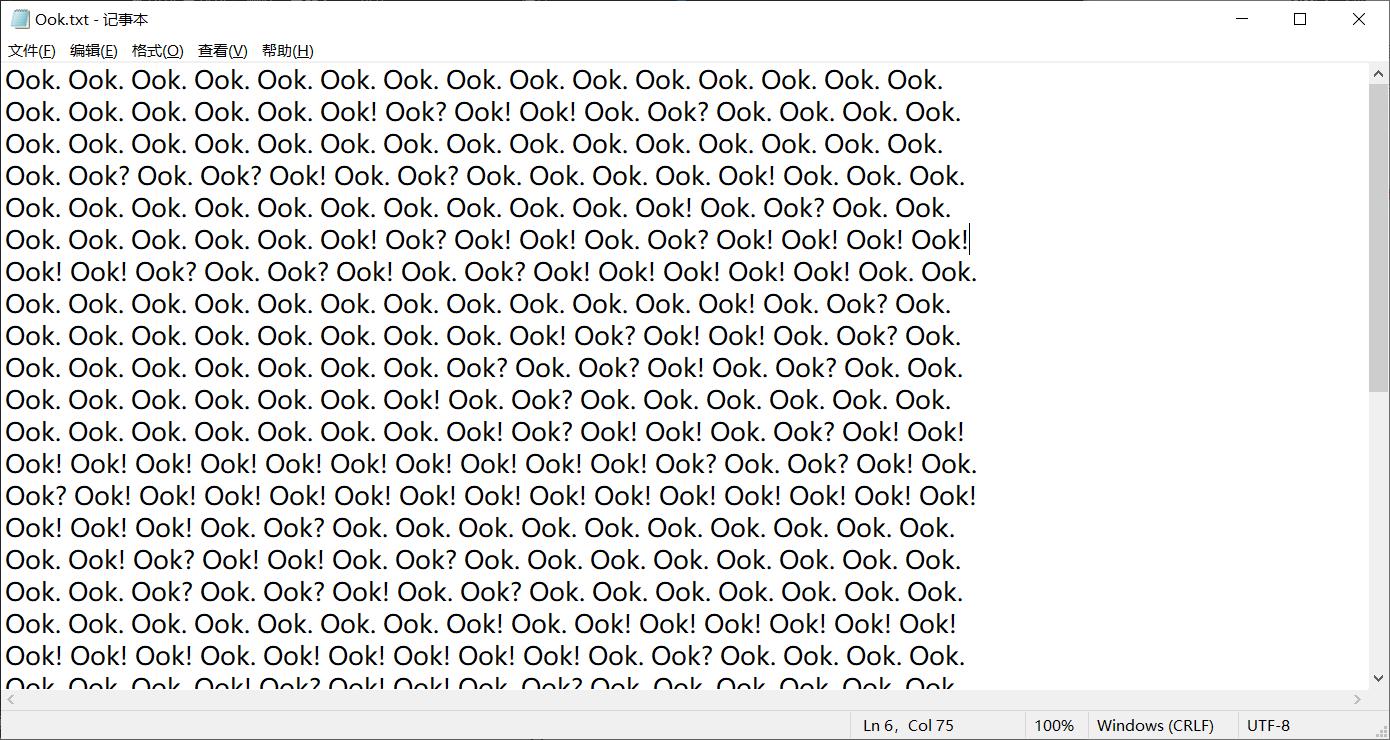
在线编解码工具

4.Quoted-Printable编码

Quoted-Printable编码表示“可打印字符引用”，它是多用途互联网邮件扩展（MIME）的一种实现方式。编码原理是：任何一个8位的字节值都可编码为3个字符，一个等号后跟随两个十六进制数字（0~9or A~F）

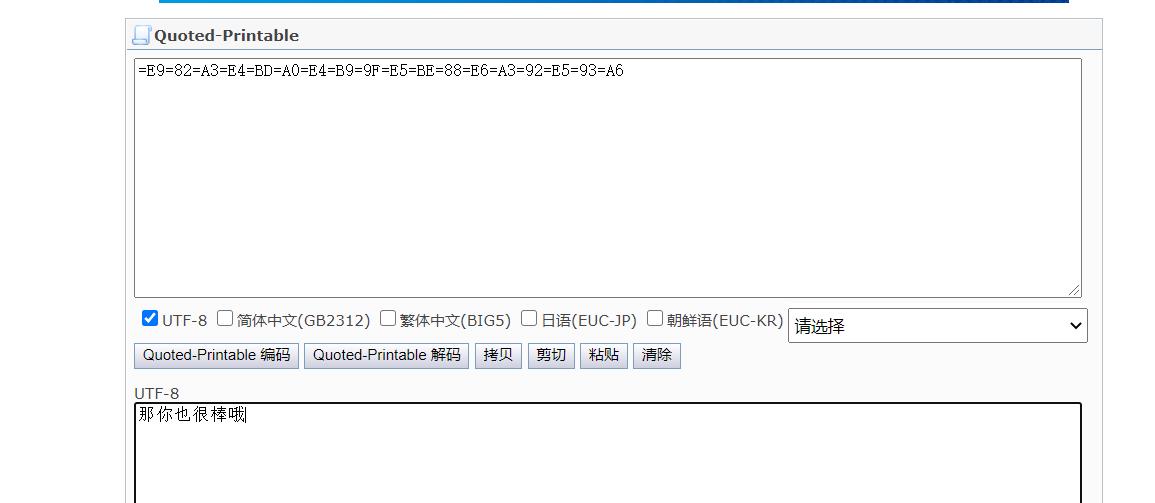
5.UUencode

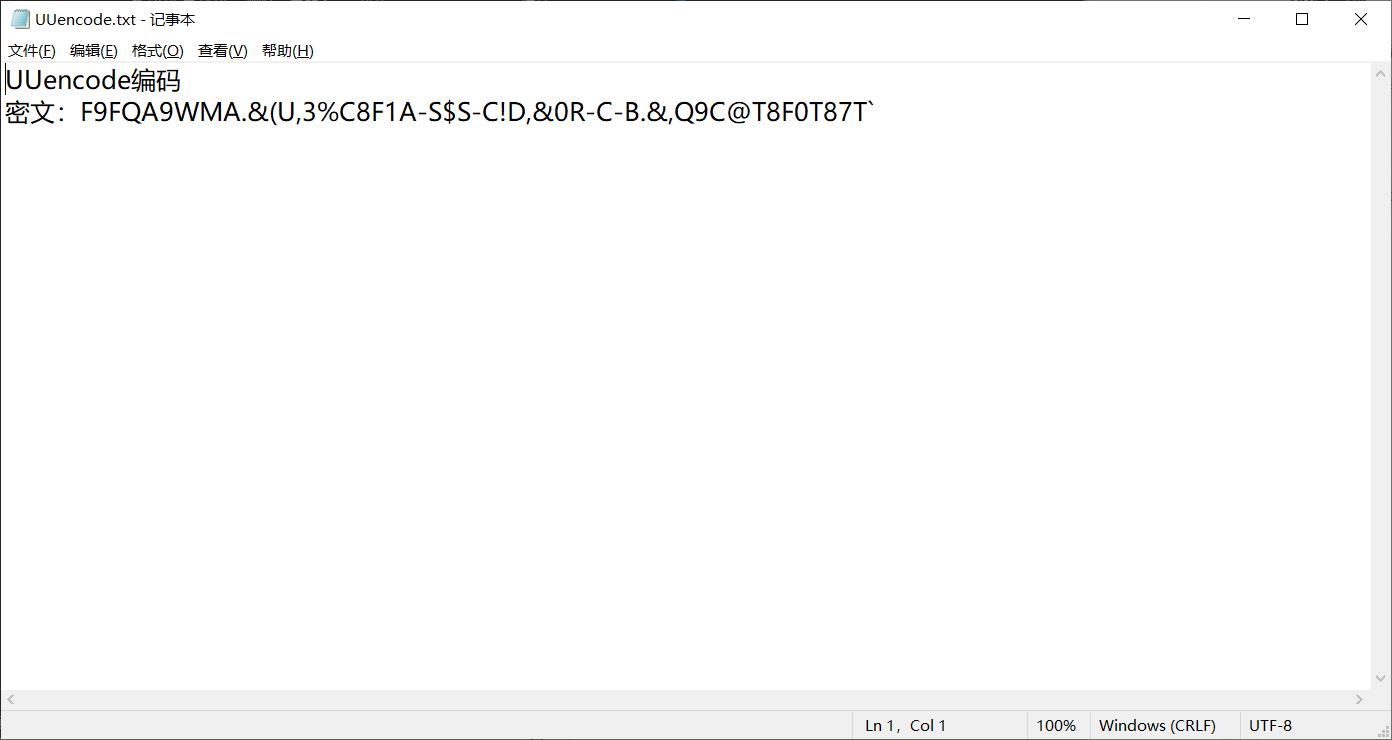
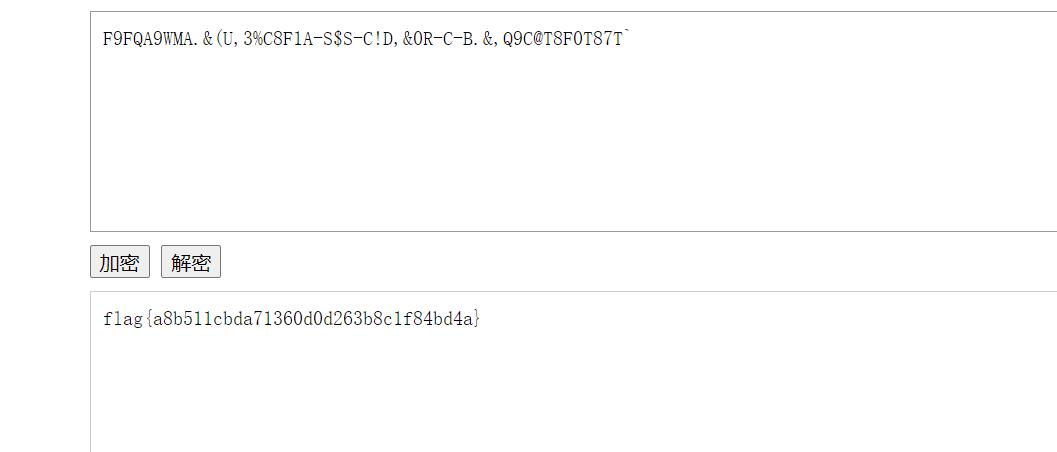
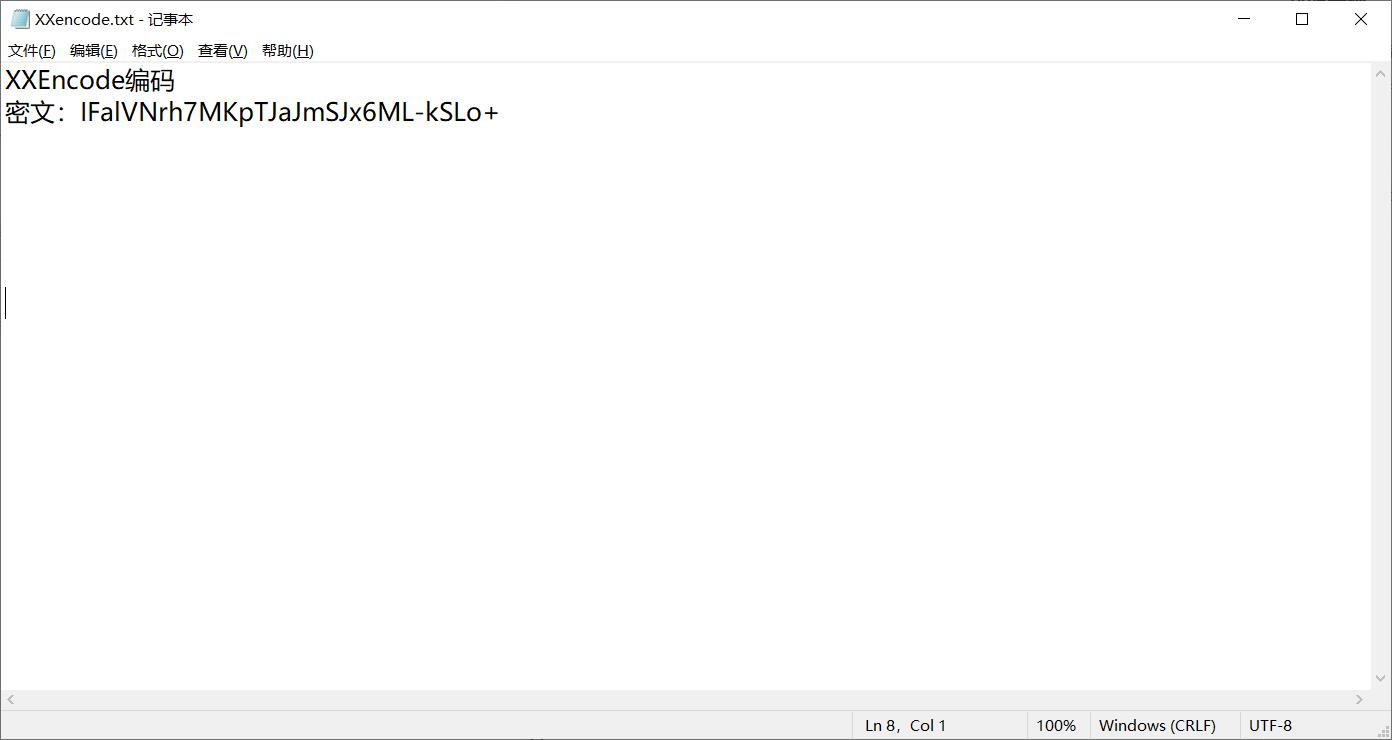
6.XXencode

古典密码

简单换位密码

根据题目提示编写解密脚本

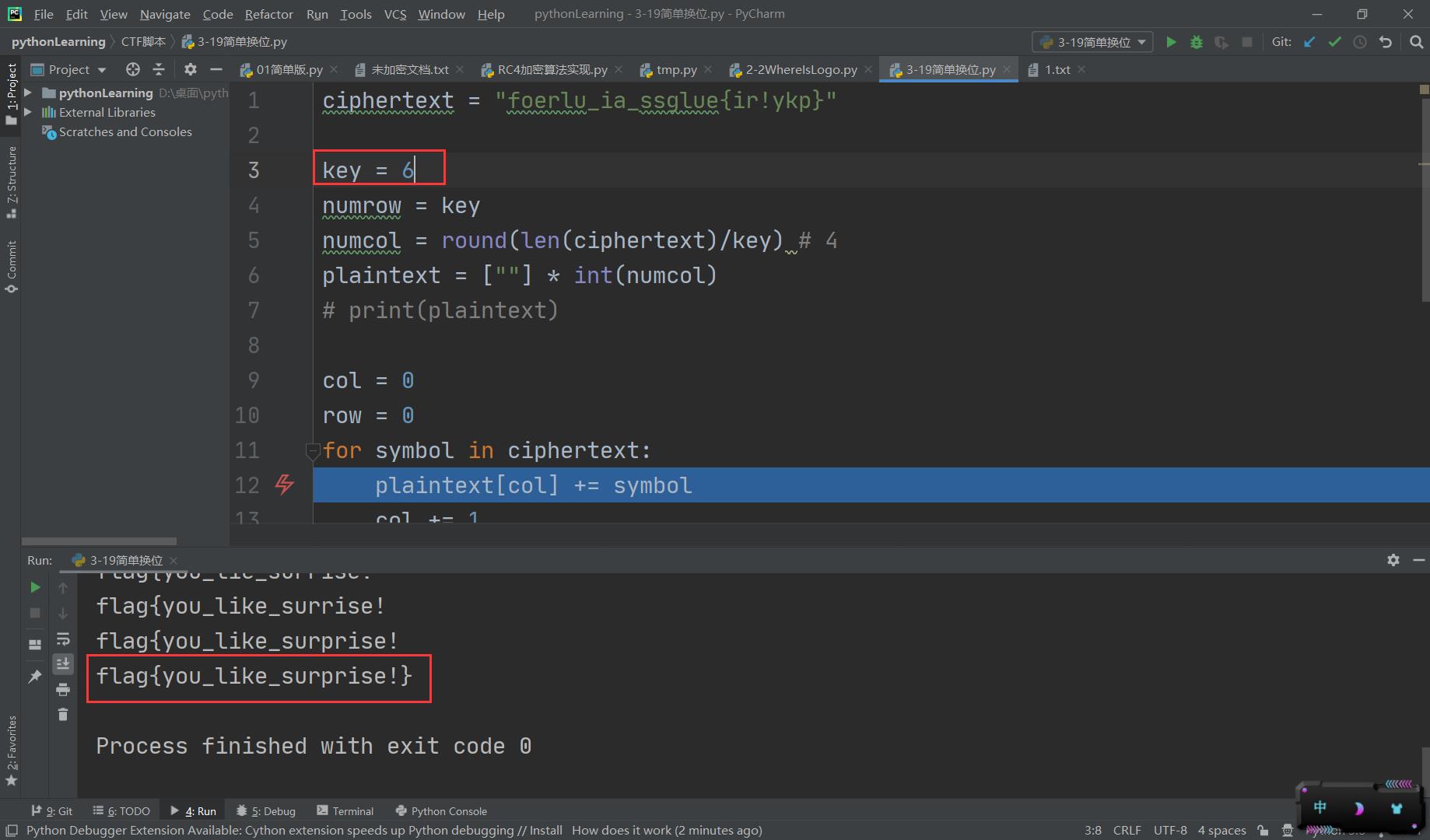
ciphertext = "foerlu_ia_ssglueir!ykp"

key = 6 # 几个一组
numrow = key
numcol = round(len(ciphertext)/key) # 4
plaintext = [""] * int(numcol)
# print(plaintext)

col = 0
row = 0
for symbol in ciphertext:
    plaintext[col] += symbol
    col += 1
    # print(plaintext)
    #
    if col == numcol:
        col = 0
        row += 1
        # print(row,plaintext)
    print(''.join(plaintext))

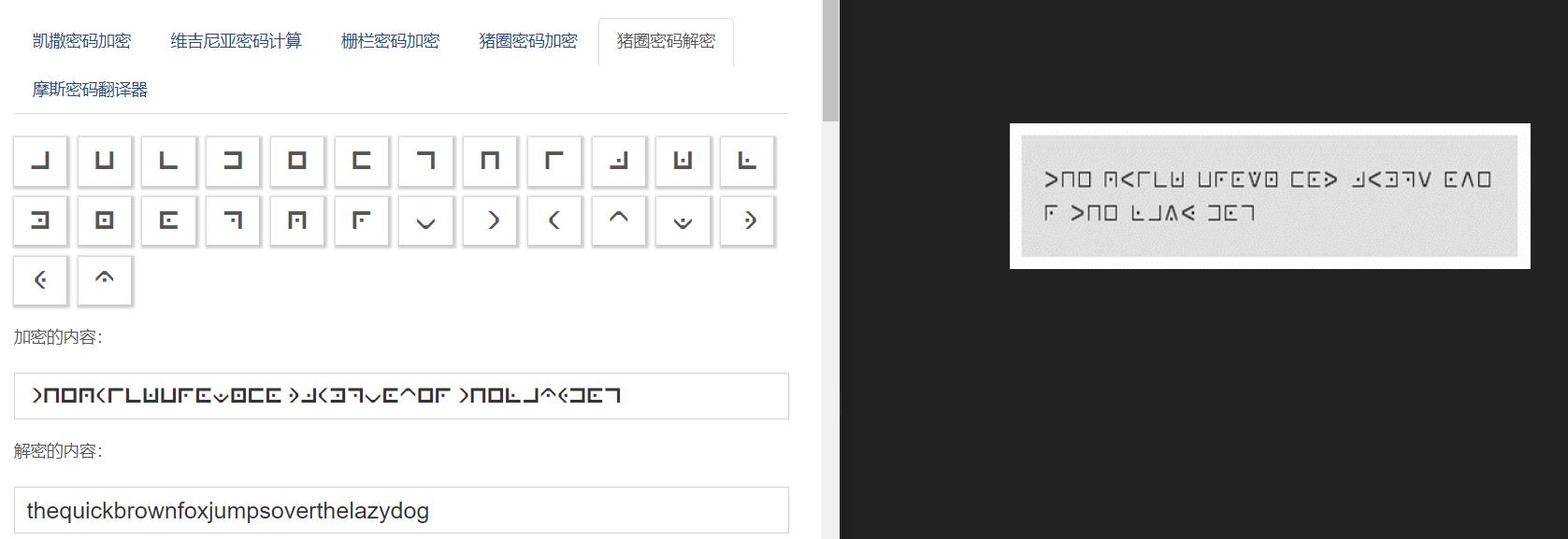
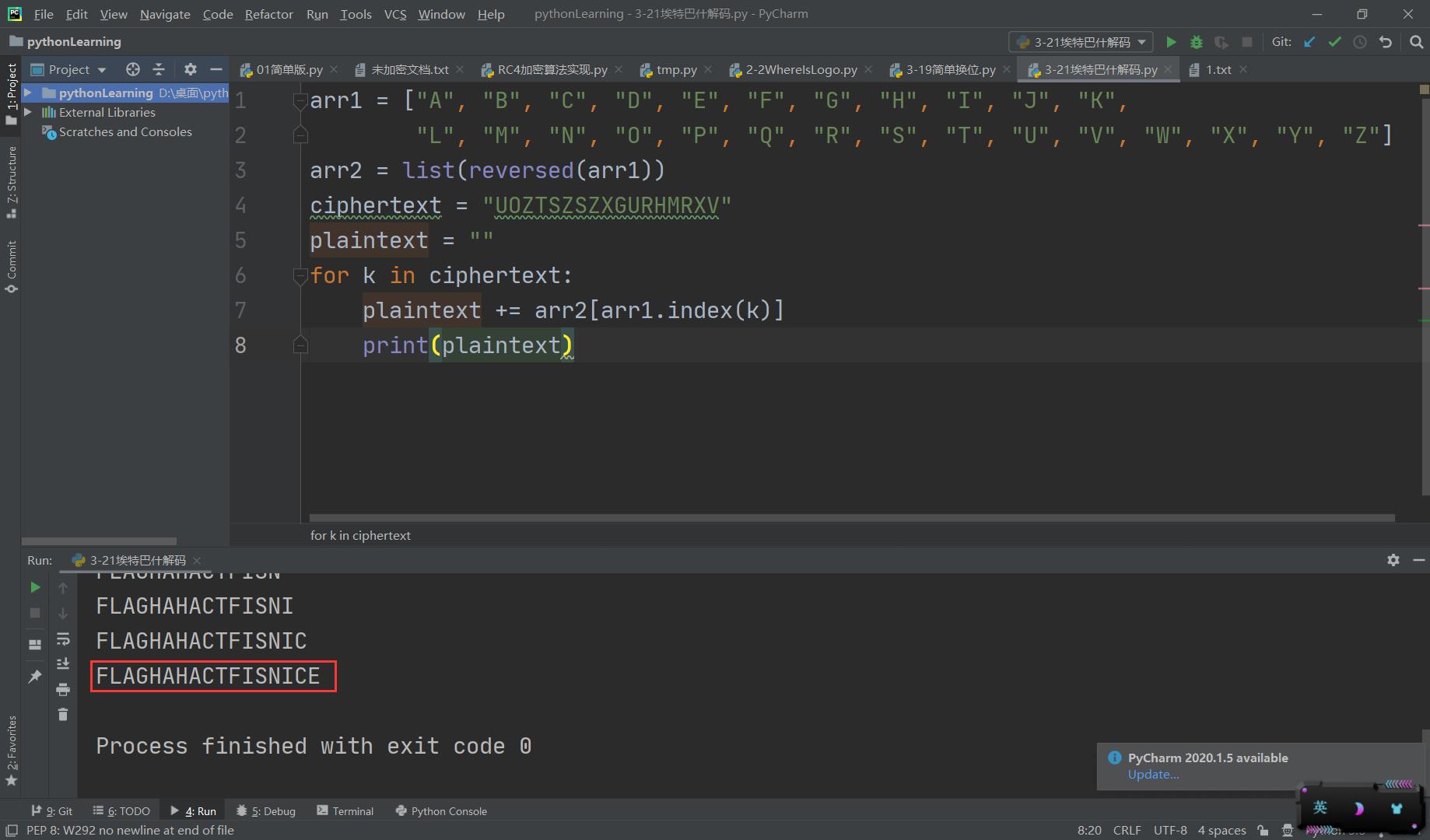
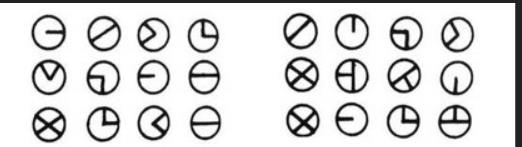
猪圈密码

看到题目想到猪圈密码，按照对应关系解密

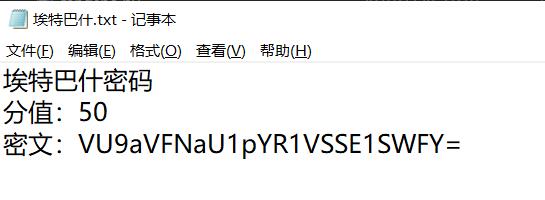
埃特巴什密码

首先看像base64编码

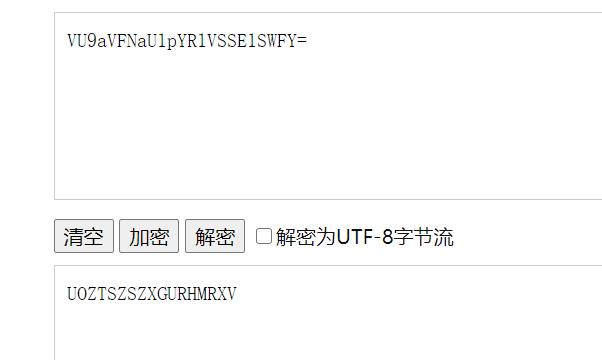
自己写一个脚本

arr1 = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K",
        "L", "M", "N", "O", "P", "Q", "R", "S", "T", "U", "V", "W", "X", "Y", "Z"]
arr2 = list(reversed(arr1))
ciphertext = "UOZTSZSZXGURHMRXV"
plaintext = ""
for k in ciphertext:
    plaintext += arr2[arr1.index(k)]
    print(plaintext)

夏多密码

对应解码就行

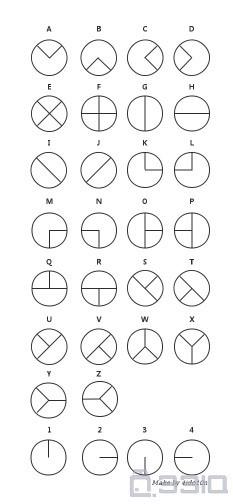
当铺密码

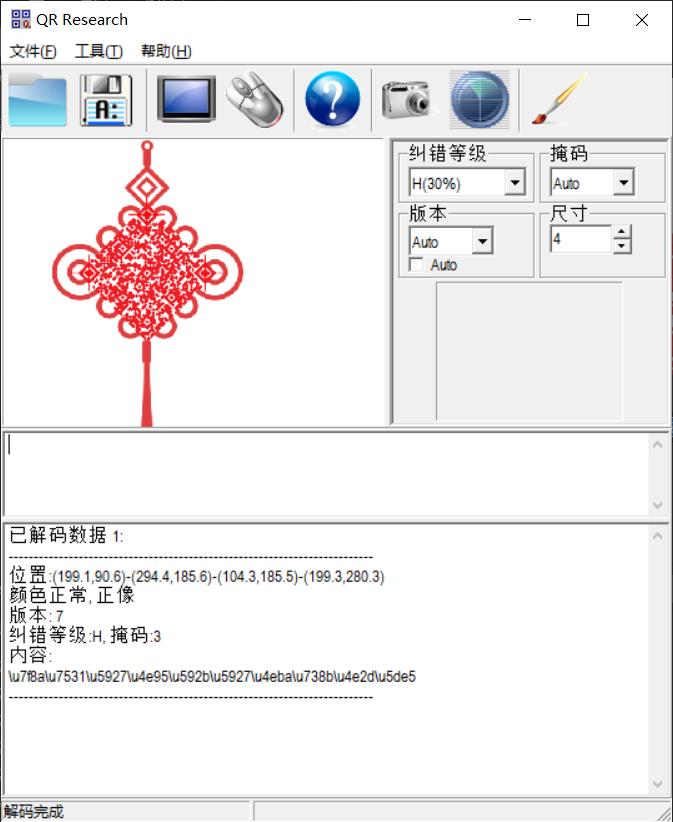
得到 9 1 5 8 7 5 3 6 2 4，不正确
通过binwalk发现图片中还有压缩文件

培根密码

1.首先看像是摩斯密码

2.因为题目说是培根，想到培根密码

九宫格密码

因为是手机收到的，所以猜测和手机有关

书上说flagsimple，但是我咋凑不出来呐？

凯撒大帝

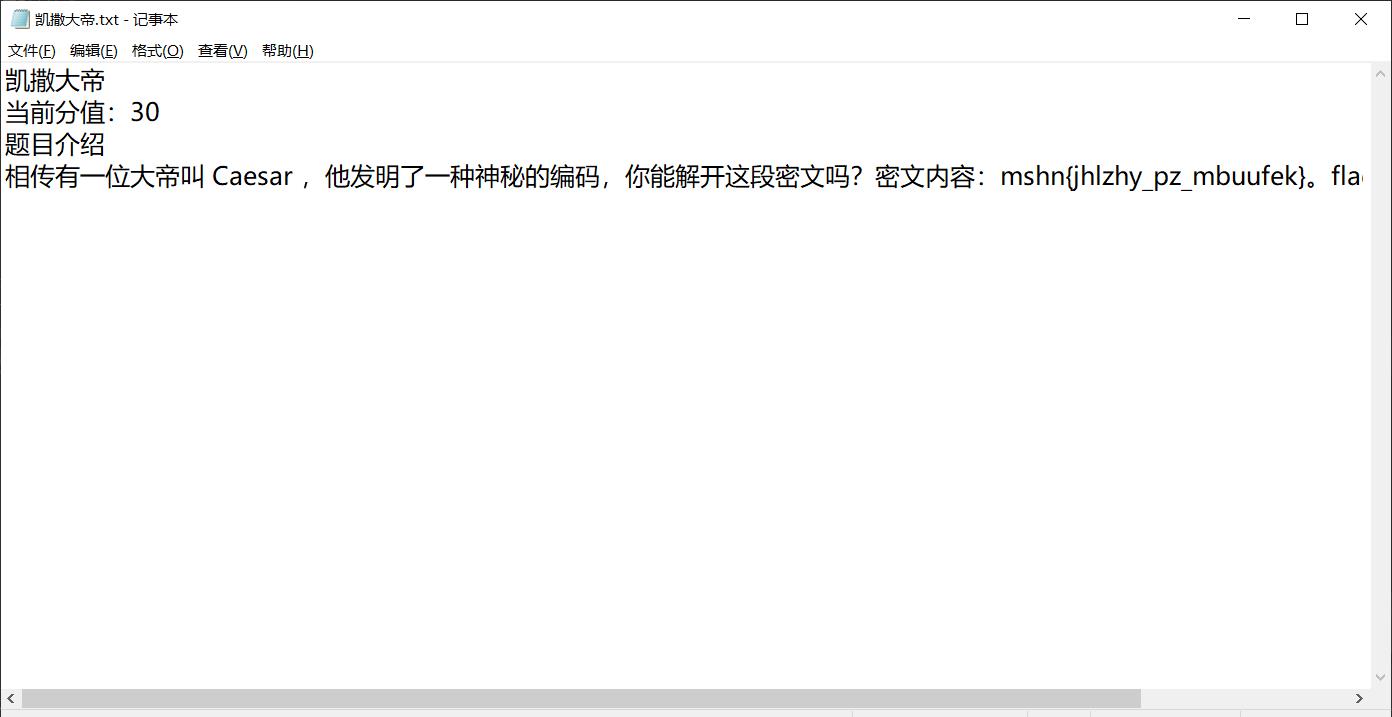
写个脚本

cipher = "mshnjhlzhypzmbuufek" # mshnjhlzhy_pz_mbuufek
# flagcaesarisftnnxwd flagcaesar_is_ftnnxwd
# print(ord("a"),ord("z")) 97 122
for n in range(1,26):
    tmp = []
    for i in cipher:
        # 使用了三目运算
        tmp.append(chr(ord(i)-n if ord(i)-n >= 97 else 122 - n + ord(i) - 97))
    print(''.join(tmp))

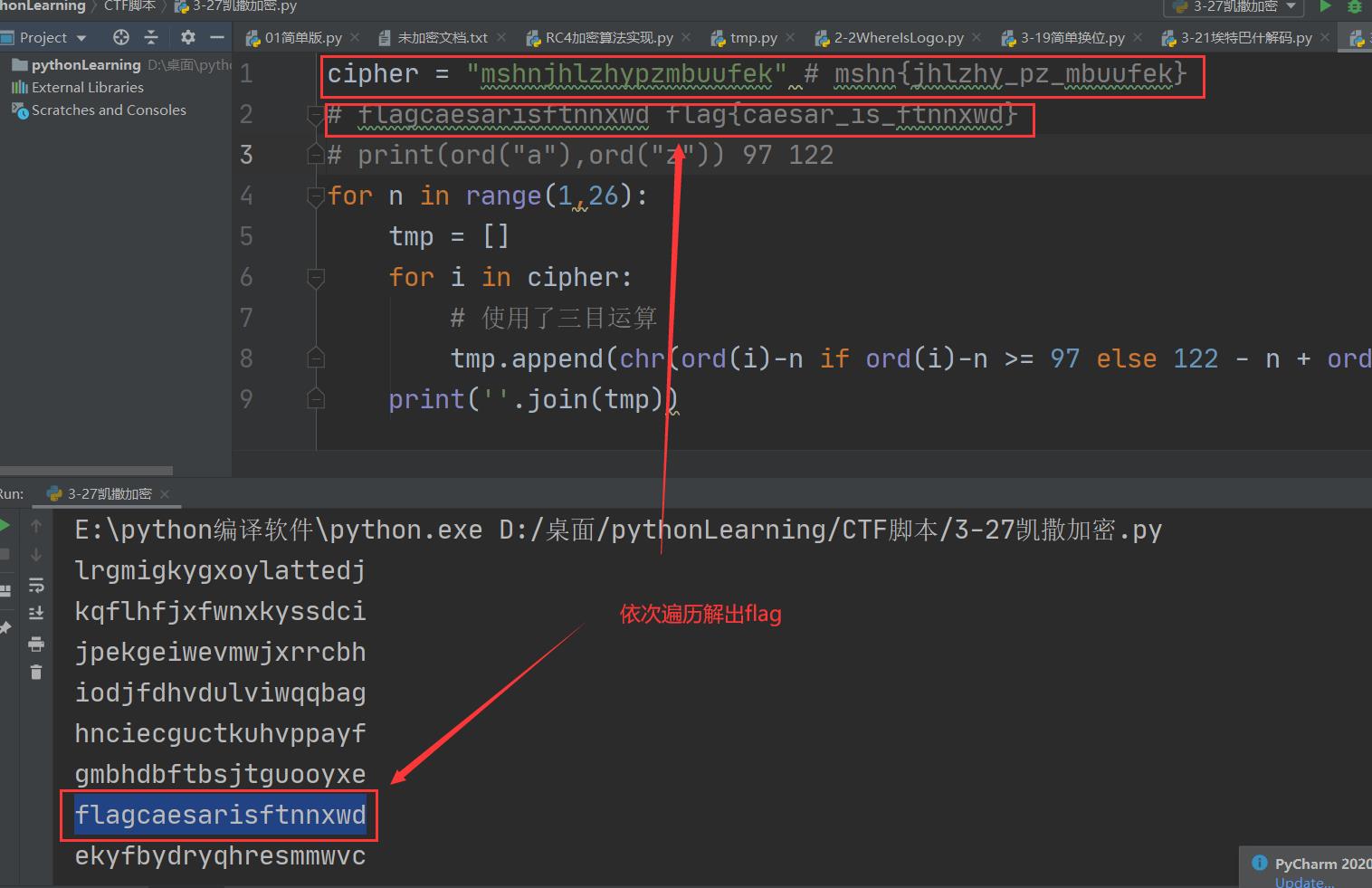
维吉尼亚密码

尝试了一下

Rabbit密码

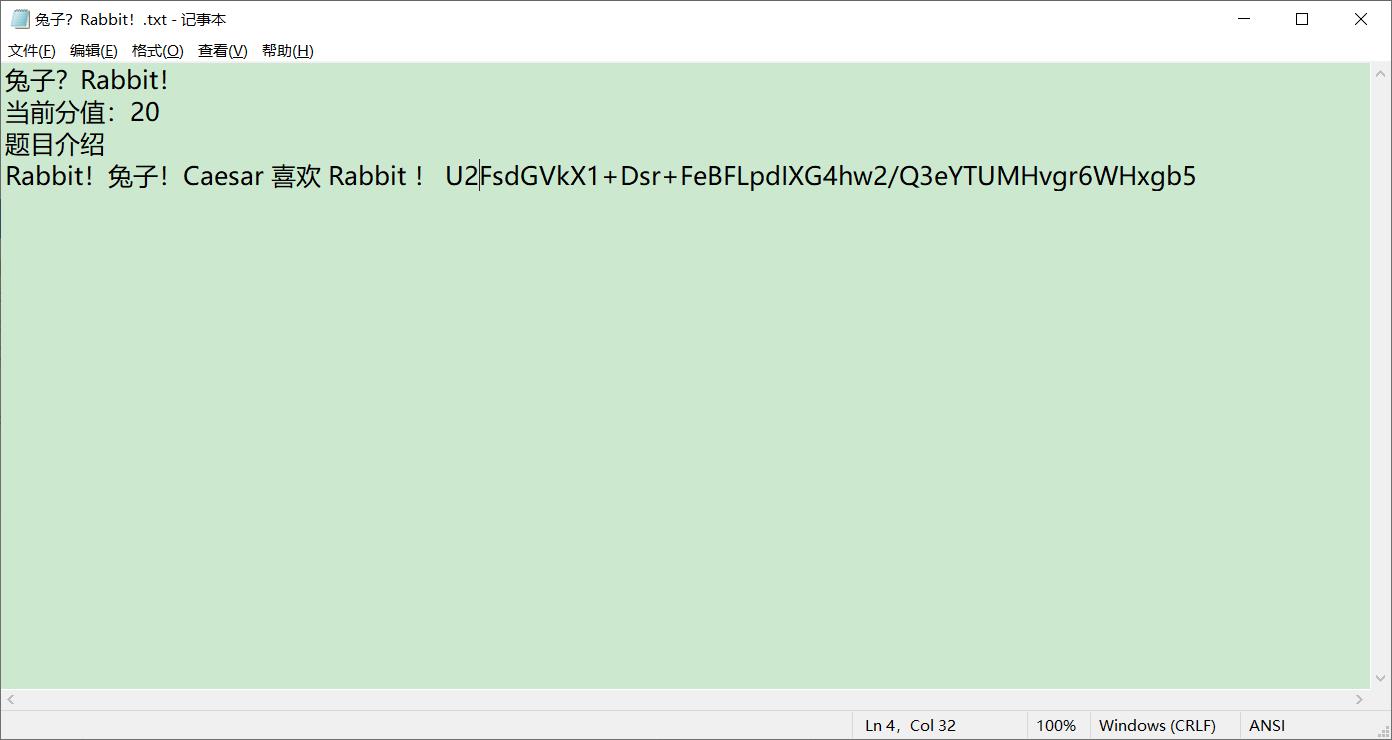
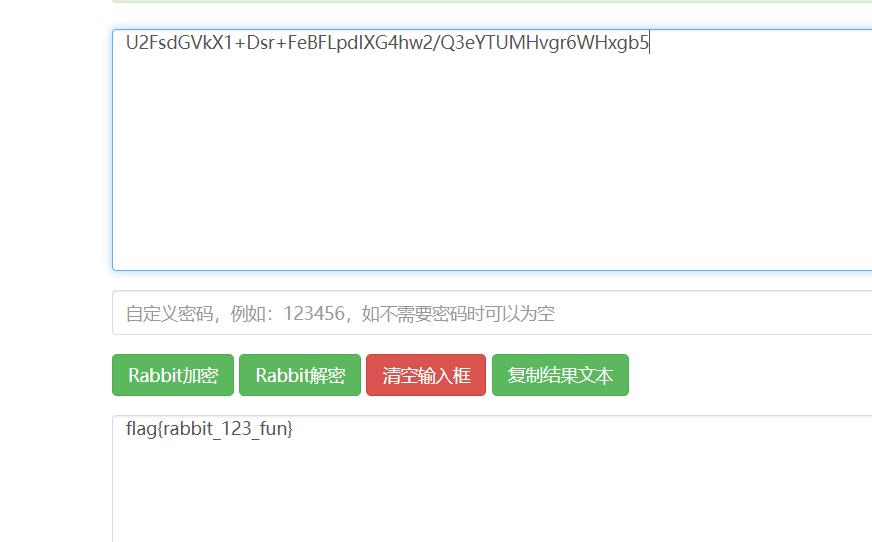
Rot13密码

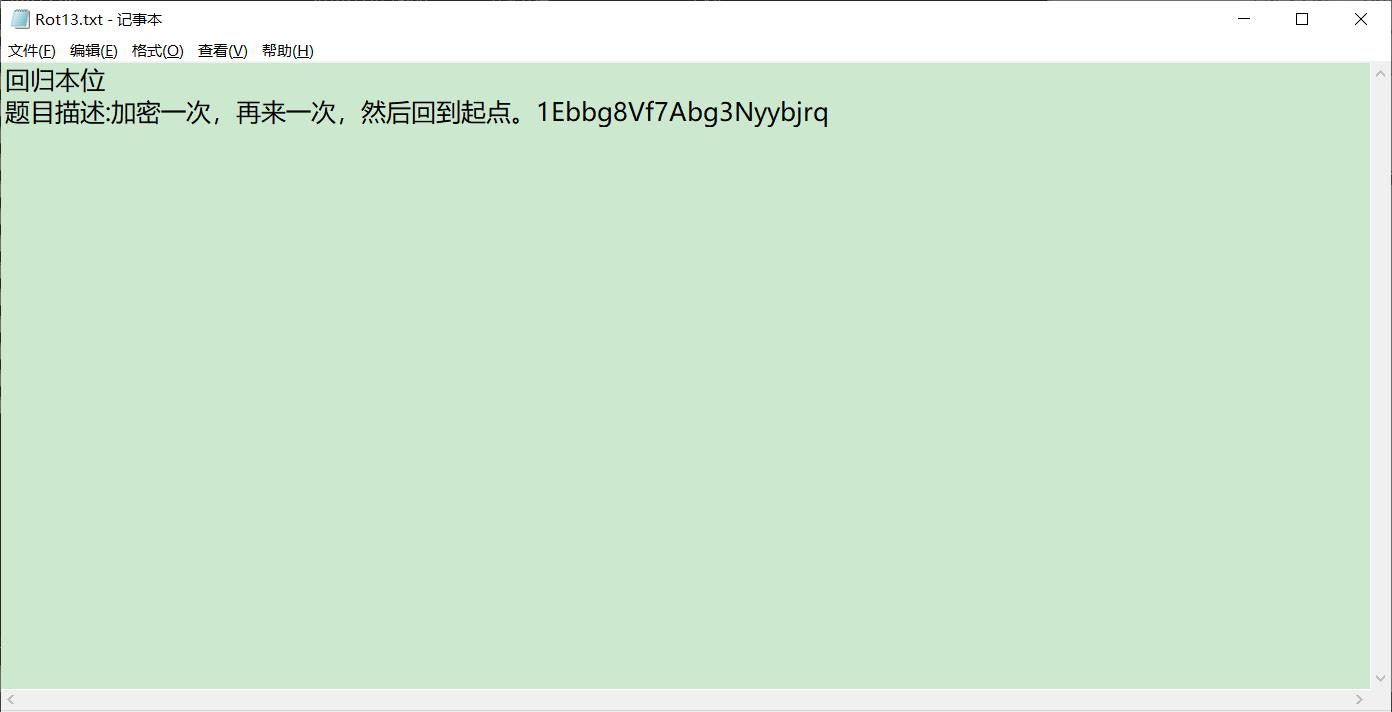
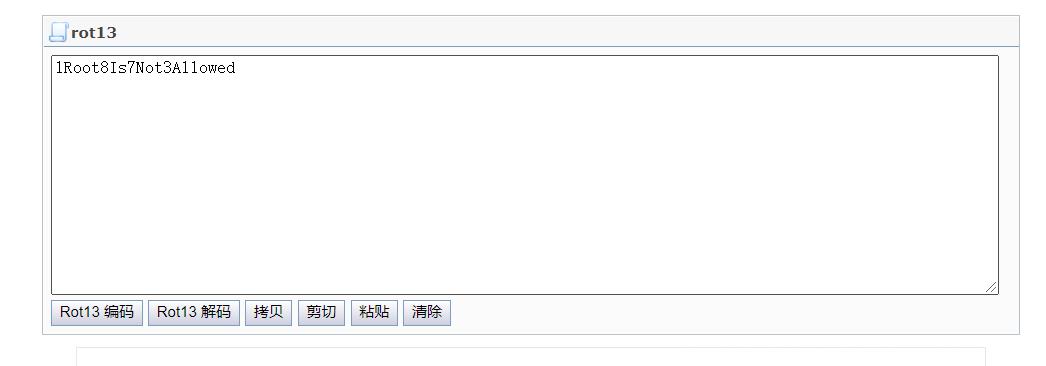
就是凯撒加密移位13

栅栏之困

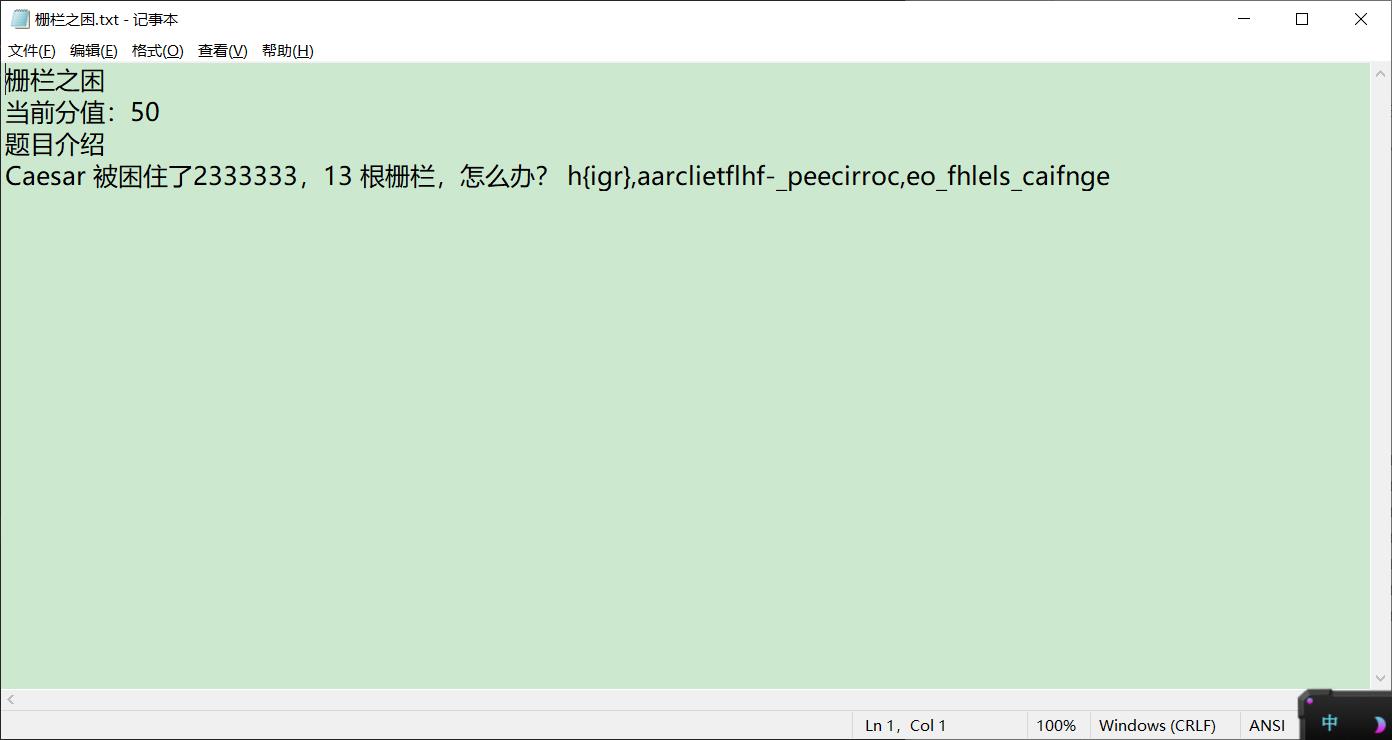
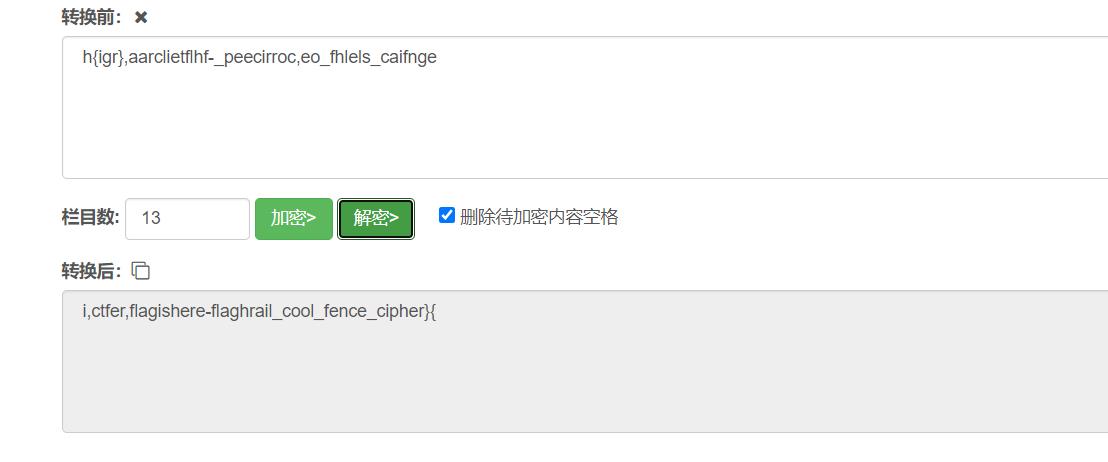
看看题，凯撒被13栅栏用栅栏解密，间隔13

关于同余方程、欧拉定理、乘法逆元、定义在Zm上的矩阵求逆

参考：https://blog.csdn.net/Pioo_/article/details/110390802

这篇讲的还是蛮清楚的

1.模同余

模同余：给定一个正整数m，如果两个整数a和b满足a-b能够被m整除，即(a-b)/m得到一个整数，那么就称整数a与b模m同余，记作a≡b(mod m)。对模m同余是整数的一个等价关系。
例如：
3被2除余1

5被2除余1

3，5 被2除有相同的余数

所以 3 同余 5 模 1 ，记做：3 ≡ 5 (mod 1)

同余的一些性质

3.欧拉函数和欧拉定理

自己去看参考文章吧我就直接乘法逆元了

希尔密码

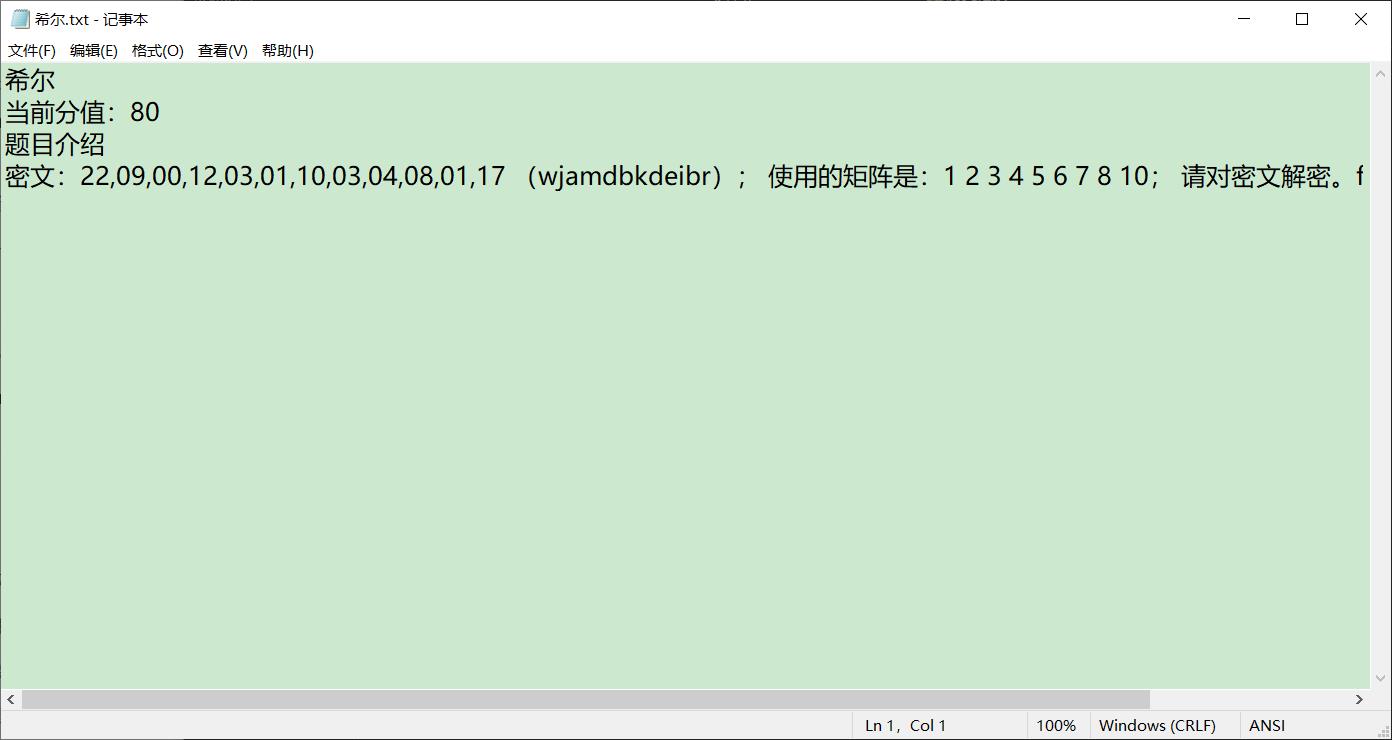
仿射密码

参考：https://blog.csdn.net/Pioo_/article/details/110235362

注意哈不是等号是三等号

还是看不懂的就看看参考文章吧！！！

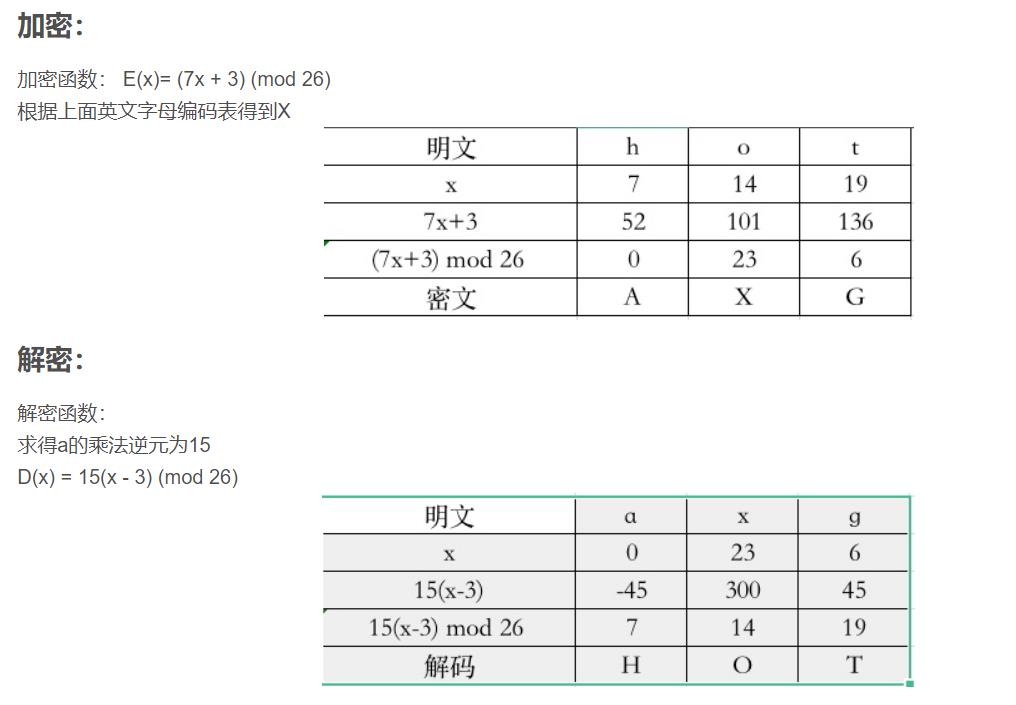
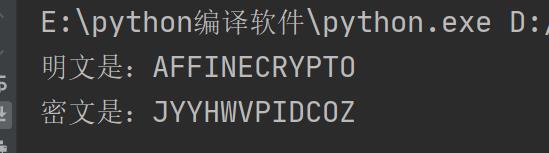
代码

'''
仿射密码K = (a,b)
加密函数是E(x)= (ax + b) (mod 26)
解密函数为D(x) = (a^-1)(x - b) (mod 26)，其中a^-1是a的乘法逆元
'''

def fangsheEncode(a, b, e):
    cipher = []
    for i in e:
        tmp = chr(((ord(i) - 65) * a + b) % 26 + 65) # a ascii 97
        cipher.append(tmp)
    print("密文是：" + "".join(cipher).upper())
# 遍历求乘法逆元
def get_multiplicative_inverse(a):
    for i in range(0,100):
        if(a * i % 26 == 1):
            # print(i)
            return i


以上是关于[CTF从0到1学习] 二CTF 密码学的主要内容，如果未能解决你的问题，请参考以下文章 
 [CTF从0到1学习] 二CTF 密码学
 [CTF从0到1学习] 二CTF 密码学
 [CTF从0到1学习] 二CTF WEB安全
 [CTF从0到1学习] 二CTF WEB安全
 [CTF从0到1学习] 二CTF WEB安全
 CTF---密码学入门第四题 困在栅栏里的凯撒

[CTF从0到1学习] 二CTF 密码学

密码学

文章目录

概述

密码学基本概念

密码学的历史与发展

第一阶段（1949年前） 古典密码发展阶段

第二阶段：近代密码阶段（1949~1976）

现代密码学阶段（1976~至今）

现代密码学的主要发展方向

密码体制分类

密码攻击

算法的安全性

编码与密码

编码基础

ASCII

unicode

BASE64

古典密码学

单表代换密码

凯撒密码

移位密码

仿射密码

多表代换密码

polybius密码（棋盘密码）

vigenere密码

其他类型密码

培根密码

栅栏密码

摩斯密码

CTF中奇怪密码

倒序加密

电脑键盘密码

键盘密码

手机键盘加密

当铺密码

猪圈密码

对称加密

CTF Wp

编码解码

1.AAencode

2.brainfuck

3.Ook

4.Quoted-Printable编码

5.UUencode

6.XXencode

古典密码

简单换位密码

猪圈密码

埃特巴什密码

夏多密码

当铺密码

培根密码

九宫格密码

凯撒大帝

维吉尼亚密码

Rabbit密码

Rot13密码

栅栏之困

关于同余方程、欧拉定理、乘法逆元、定义在Zm上的矩阵求逆

希尔密码

仿射密码

第一阶段（1949年前）古典密码发展阶段