2022年ACM暑假集训个人排位赛A-F题解

Posted 2023-02-04 ZZXzzx0_0

A: 剩余的数量

题意：
现有S和T字符串,其数量分别是A和B
现给你一个字符串U，U=S或者U=T，使其数量-1
问S和T现在的数量是多少
思路：
模拟
时间复杂度：$O1$

#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6 + 10 ;
string a , b , s ;
int ca , cb ;

int main()

    cin >> a >> b >> ca >> cb >> s ;
    if(a == s) ca -- ;
    else cb -- ;
    cout << ca << " " << cb << "\\n" ;
    
    return 0 ;

B: 替换字符

题意：
给你一个字符串，将其中所有字符都替换为x并输出
思路：
模拟
时间复杂度：$On$

#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6 + 10 ;

int main()

    string s ;
    cin >> s ;
    for(auto i : s) cout << 'x' ;
    return 0 ;

C: 相同或者不同

题意：
给你n个数的数组
$a_1$ $a_2$ …$a_n$
问是否所有数都不一样
是输出YES
否则输出NO
思路：
用map记录一下每个数的出现次数
只要有一个数的出现次数大于等于2次
输出NO即可
否则输出YES
时间复杂度：$Onlogn$

#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6 + 10 ;
map<int,int> q ;
int f , n , x ;

int main()

    cin >> n ;
    while(n --)
    
        scanf("%d",&x) ;
        q[x] ++ ;
        if(q[x] >= 2) f = 1 ; 
    
    puts((f == 1 ? "NO" : "YES")) ;
    
    return 0 ;

D: 排成一行的骰子

题意：
我们把 n个骰子从左到右排成一行
左侧第 i 个骰子显示$p_i$ , $p_i$表示这个骰子可以抛出的点数范围为[1,$p_i$]，每个点抛出的概率相等
我们将选择k个相邻的骰子，分别投掷每个骰子，并计算所示数字的总和。
查找此总和的期望值的最大可能值。
思路：
对每个骰子来说,每个点数抛出的概率相等为$1/p_i$
所以每个骰子的点数的期望为
$$1/p_i\ast (1+2+3+.....+p_i)$$
$$1/p_i\ast (p_i)\ast (p_i+1)/2$$
化简得
$$(1+p_i)/2$$
题目求的是连续k个骰子的期望和的最大值
用前缀和优化一下即可

时间复杂度：$On$

#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6 + 10 ;
int n , k ;
double a[N] , s[N] ;

int main()

    cin >> n >> k ;
    for(int i = 1 ; i <= n ; i ++)
    
        cin >> a[i] ;
        s[i] = s[i - 1] + (a[i] + 1.0) / 2.0 ;
    
    
    double v = 0 ;
    for(int i = 1 ; i + k - 1 <= n ; i ++)
    
        v = max(v , s[i + k - 1] - s[i - 1]) ;
    
    
    printf("%.12lf",v) ;
    
    return 0 ;

E: 到处都是0

题意：
求1到N（包括1和N）之间的整数的数目，
这些整数恰好包含K个非0数字
思路：

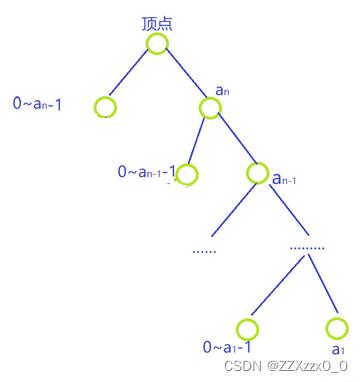
首先我们把$n$的每一位保存到一个数组里面

我们从这个数的最高位往最低位遍历

假设现在遍历到了最高位
填$0$到$a_n-1$的任意数字,记为x
x_ _ _ _ _ _ _ _ _ 后面有n-1个位置
通过动态规划可以计算出来

我们用$f[i][j][k]$来表示一共有$i$位,最高位填$j$,当前一共有$k$个非$0$数字的方案数
状态转移方程为
$$f[i+1][z][k+(z!=0)]+=f[i][j][k];$$

x_ _ _ _ _ _ _ _ _ 后面有n-1个位置
所以该方案数为$f[n][x][k]$
表示一共有$n$位,最高位填的是$x$,有$k$个非$0$数字的情况下的方案数

填完$a_n$之后,继续往这颗树上继续填,直到不能填为止

时间复杂度：$O(100n)$

#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
#define int long long
using namespace std;

const int N = 110;

int f[N][10][5] , m ;
char s[N] ;

void init()  // 求动态规划方程

    for (int i = 0; i <= 9; i ++ ) f[1][i][(i != 0)] = 1;

    for (int i = 1; i <= N - 10; i ++ )
        for (int j = 0; j <= 9; j ++ )
            for(int z = 0 ; z <= 9 ; z ++)
                for(int k = 0 ; k <= 3 ; k ++)
                    f[i + 1][z][k + (z != 0)] += f[i][j][k] ;
            


void dp()

    vector<int> nums;
    
    cin >> s + 1 >> m ;
    for(int i = strlen(s + 1) ; i >= 1 ; i --)
        nums.push_back(s[i] - '0') ;

    int res = 0;
    int last = 0;  // last表示之前高位填的数中有多少个非0数
    for (int i = nums.size() - 1; i >= 0; i -- )
    
        int x = nums[i];     // 当前位的数字
        if(last > m) break ;  // 高位已经填了k+1个非0数 直接break即可
        
        //cout << i << " " << x << " " << last << '\\n' ;
        
        for(int j = 0 ; j < x ; j ++)
            res += f[i + 1][j][m - last] ;
        
        //cout << res << '\\n' ;
        
        if(x != 0) last ++ ;  // 统计高位的非0数

        if (!i && last == m) res ++ ;  // 如果这个数本身也符合题意  答案++
    

    cout << res << '\\n' ;


signed main()

    init();
    
    dp() ;
    
    return 0;

F: 路径数目

题意：

小梁站在一个二维平面上。在一次操作中，他可以在正x方向移动1，或在正y方向移动1。
让我们定义一个函数f（r，c），如下所示：
$f(r，c)$=从点（0,0）到点（r，c）的路径数
现在给你$r1,c1,r2,c2$
求
${\sum }_{i=r1}^{r2}{\sum }_{j=c1}^{c2}f(i,j)$

思路：

首先,从$(0,0)$走到$(i,j)$的方案数为$以上是关于2022年ACM暑假集训个人排位赛A-F题解的主要内容，如果未能解决你的问题，请参考以下文章$

2022年ACM暑假集训个人排位赛A-F题解

2022.07.15 暑假集训 个人排位赛

2022.07.13 暑假集训 个人排位赛

2022.07.14 暑假集训 个人排位赛

2022.07.14 暑假集训 个人排位赛

2022.07.14 暑假集训 个人排位赛