C++进阶：二叉树进阶二叉搜索树的操作和key模型key/value模型的实现 | 二叉搜索树的应用 | 二叉搜索树的性能分析

Posted 2023-02-04 跳动的bit

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了C++进阶：二叉树进阶二叉搜索树的操作和key模型key/value模型的实现 | 二叉搜索树的应用 | 二叉搜索树的性能分析相关的知识，希望对你有一定的参考价值。

【写在前面】

从这里开始 C++ 的语法就告一段落了。二叉树在前面的数据结构和算法初阶中就讲过，本文取名为二叉树进阶是因为：

二叉树进阶有着承上启下的作用，承上就是借助二叉搜索树，对二叉树初阶部分进行收尾总结，启下就是 map 和 set 的特性需要先铺垫二叉搜索树，二叉搜索树也是一种树形结构。
对于二叉搜索树的特性了解，有助于更好的理解 map 和 set 的特性。
二叉树中部分面试题稍微有些难度，在二叉树初阶讲解不适合。
有些 OJ 题使用 C 语言实现比较麻烦。

我们之前说过，普通二叉树单纯的存储数据价值不大，因为仅仅是单纯的存储数据，你不如去使用顺序表和链表这样友善的多。它一定要套一种应用场景，二叉树的其中一个重要的应用场景就是我们本文中要学习的二叉搜索树。

一、二叉搜索树

💦 概念

二叉搜索树又称搜索二叉树或二叉排序树 (如果你对下图的二叉搜索树中序遍历，你会发现它是有序并且升序的，这是它的附带特征，实际我们要排序一组数据也不会使用它，因为其底层需要存储值以外的东西，以此来进行关联，后面加入平衡后还会存储平衡因子、颜色等，那排序直接使用 vector 不香嘛，它的存储是很纯粹的，注意搜索树这里严格来说并不是排序，而是排序 + 去重，因为搜索树一般不支持冗余，所以一般要排序也不会真的使用到搜索树，除非数据就在其中，恰好要排序 + 去重)，我们当前学习的搜索二叉树一般是不允许修改的，不过下面我们会学习搜索二叉树的 key/value 模型，它支持修改，改的是 value。它或者是一棵空树，或者是具有以下特性的二叉树：

若它的左子树不为空，则左子树上所有的节点的值都小于根节点的值。
若它的右子树不为空，则右子树上所有的节点的值都大于根节点的值。
它的左右子树也分别都是二叉搜索树。

💦 二叉搜索树操作

1、查找

以前我们的普通二叉树查找时通常都是暴力查找，此时二叉搜索树的优势就体现了。

若根节点不为空：

如果 (根节点 key == 查找 key)，返回 true；

如果 (根节点 key > 查找 key)，在其左子树查找；

如果 (根节点 key < 查找 key)，在其右子树查找；

否则，返回 false；
二叉搜索树结构查找一个值最多查找高度次。

2、插入

这个数据所插入的位置是唯一的，插入数据后，要保证二叉搜索树。注意默认情况下，二叉搜索树是不允许冗余的，比如下图不能再插入 8，但是后面 STL 对其改造后允许冗余。

插入具体过程如下：

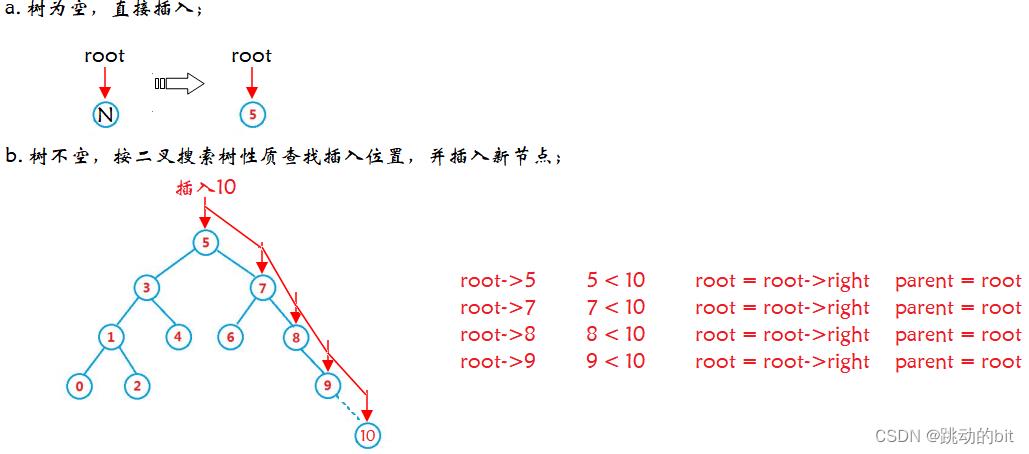
3、删除

删除才是二叉搜索树比较麻烦的，也是值得我们去探讨的。删除数据后，要保证二叉搜索树。

首先查找删除的元素是否在二叉搜索树中，如果不存在，则返回，否则要删除的结点可能分下面四种情况：

a. 要删除的节点无孩子节点；

b. 要删除的节点只有左孩子节点；

c. 要删除的节点只有右孩子节点；

d. 要删除的节点有左右孩子节点；

a 的删除没啥，找到目标位置释放，并把目标位置的父亲的左或右置空；b 和 c 也还好，找到目标位置后，把目标位置的父亲的左或右关联到目标位置的孩子，再把目标位置释放；d 的删除有点啥，这里使用替代删除，也就是找左树的最大节点或者右树的最小节点，且左树的最大节点一定是最右节点，右树的最小节点一定是最左节点 (左右树只有一个节点除外)，找到目标位置、找到替代位置后，把目标位置替换，把替代位置的父亲与替代位置的孩子关联，最后再把替代位置释放；看起来待删除节点有 4 种情况，实际情况 a 可以与情况 b 或者 c 合并起来，因此真正的删除过程应该如下：

情况 ab，删除该节点且使被删除节点的双亲节点指向被删除节点的左孩子节点；
情况 ac，删除该节点且使被删除节点的双亲节点指向被删除节点的右孩子节点；
情况 d，在它的右子树中寻找中序下的第一个节点 (关键码最小)，用它的值补到被删除节点中，再来处理该节点的删除问题；

💦 二叉搜索树key模型的实现

1、基本结构

namespace KEY

	template<class K>
	struct BSTreeNode
	
		BSTreeNode<K>* _left;
		BSTreeNode<K>* _right;
		K _key;
	;
	template<class K>
	class BSTree
	
		typedef BSTreeNode<K> Node;
	public:
	private:
		Node* _root = nullptr;
	;

以前我们定义模板时命名都是 T，表示 type。而这里我们用 K，表示 key，它是 key 模型，下面我们还会变形一下讲 key/value 模型，搜索树通常要演化这两种形态，它们是常用的搜索模型。

2、Insert

bool Insert(const K& key)

	//空树,直接插入
	if(_root == nullptr)
	
		_root = new Node(key);
		return true;
	
	//查找要插入的位置
	Node* cur = _root;
	while(cur)
	
		if(cur->_key < key)//往右子树查找
		
			cur = cur->_right;	
			
		else if(cur->_key > key)//往左子树查找
		
			cur = cur->_left;	
		
		else
		
			return false;//默认不支持冗余	
		
	
	//插入? ? ?
	cur = new Node(key);
	return true;

这里在找到要插入的位置后，new 了一个节点，并不代表已经插入成功，因为这个节点没有与父亲关联起来，且出了作用域就会内存泄漏，因为 cur 是唯一能标识这个节点的位置，而 cur 是一个局部变量，所以必须在 cur 销毁之前，将它们进行关联。

✔ 修正

bool Insert(const K& key)

	//空树,直接插入
	if(_root == nullptr)
	
		_root = new Node(key);
		return true;
	
	//查找要插入的位置
	Node* parent = nullptr;
	Node* cur = _root;
	while(cur)
	
		if(cur->_key < key)//往右子树查找
		
			parent = cur;
			cur = cur->_right;	
			
		else if(cur->_key > key)//往左子树查找
		
			parent = cur;
			cur = cur->_left;	
		
		else
		
			return false;//默认不支持冗余	
		
	
	//new节点
	cur = new Node(key);  
	if(parent->_key < cur->_key)//新节点链接到父的左还是右,还需要再比一次
	
		parent->_right = cur;//关联
	
	else
	
		parent->_left = cur;//关联
	
	return true;

3、InOrder

void InOrder(Node* root)

	if(root == nullptr)
	
		return;	
	
	InOrder(root->_left);
	cout << root->_key << " ";
	InOrder(root->_right);

这里类里成员函数里面按以前的方法写递归会陷入一个困境中 —— InOrder 需要传树的根，但是根是私有的。你可以实现一个 GetRoot，然后 main 函数里调用时 t.InOrder(GetRoot())，但是这样怪怪的，你还要把根给暴露出去。这里不就是想拿到根嘛，更好的方式是 main 函数里 t.InOrder()，成员函数里面套一层无参的 InOrder 去调用上面有参的 InOrder。此时它们俩构成函数重载，但是这样不大好，所以把有参的 InOrder 改成 _InOrder，更规范点你还可以把它定义成私有的，只供内部使用。所以一般要访问成员变量，为了封装性，需要套一层。

✔ 修正

public:
	void InOrder()
	
		_InOrder(_root);
		cout << endl;
	
private:
	void _InOrder(Node* root)
	
		if(root == nullptr)
		
			return;	
		
		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);

4、Find

Node* Find(const K& key)

	Node* cur = _root;
	while(cur)
	
		if(cur->_key < key)
		
			cur = cur->_right;
		
		else if(cur->_key > key)
		
			cur = cur->_left;	
		
		else
		
			return cur;	
		
		
	return nullptr;

Find 没有给布尔值是为了改造 key/value 结构

5、Erase

bool Erase(const K& key)

	Node* parent = nullptr;
	Node* cur = _root;
	while(cur)
	
		if(cur->_key < key)
		
			parent = cur;
			cur = cur->_right;	
			
		else if(cur->_key > key)
		
			parent = cur;
			cur = cur->_left;	
		
		else
		
			//删除
			if(cur->_left == nullptr)//ab
			
				//确定目标位置父亲的左还是右和目标位置的孩子关联(目标位置的左右孩子在外层if已经确定了)
				if(cur == parent->_left)
				
					parent->_left = cur->_right;
				
				else
				
					parent->_right = cur->_right;	
				
				delete cur;
			
			else if(cur->_right == nullptr)//ac
			
				//确定目标位置父亲的左还是右和目标位置的孩子关联(目标位置的左右孩子在外层if已经确定了)
				if(cur == parent->_left)
				
					parent->_left = cur->_left;	
				
				else
				
					parent->_right = cur->_left;	
				
				delete cur;
			
			else//d
			
				//找右树的最小节点去替代删除
				Node* minRightParent = nullptr;
				//cur->right一定不为空
				Node* minRight = cur->_right;
				//最小节点
				while(minRight->_left)
				
					minRightParent = minRight;
					minRight = minRight->_left;
				
				//替代
				cur->_key = minRight->_key;
				//minRight的左一定为空,但右不一定为空,无论是否为空,minRightParent要指向minRight的右 ? ? ?
				minRightParent->_left = minRight->_right;
				delete minRight;
			
			return true;
		
		
	return false;

在删除仅有一个孩子的节点时，也就是 ab 和 ac 情况时还需要再判断目标节点是父亲的左还是右，如果不这么做，就可能出现下面的 bug。
对于上面的代码在删除 7 时，程序会崩溃，因为 minRight 是 8，而 minRight->_left 是空，循环都没进去，minRightParent 也就没初始化喽，虽然能替代成功，但是在 minRightParent->_left 时会空指针解引用崩溃。解决方法就是定义 minRightParent 时给 cur，且释放节点之前节点的父亲和节点的孩子的关联需要再判断，之前我们认为 minRight 一定是 minRightParent 的左，其实不然。

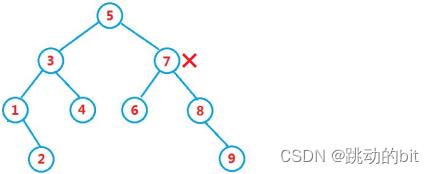
✔ 修正

else//d

	//找右树的最小节点去替代删除
	Node* minRightParent = cur;
	//cur->right一定不为空
	Node* minRight = cur->_right;
	//最小节点
	while(minRight->_left)
	
		minRightParent = minRight;
		minRight = minRight->_left;
	
	//替代
	cur->_key = minRight->_key;
	//minRight的左一定为空,但右不一定为空,minRightParent->_left不一定是minRight
	if(minRight == minRightParent->_left)//删除5,找6
	
		minRightParent->_left = minRight->_right;
	
	else//删除7,找8
	
		minRightParent->_right = minRight->_right;
	
	delete minRight;

至此，我们删除情况 ab、ac、d 都没问题，但是当我们挨个对搜索二叉树的节点删除时，却发现程序崩溃了。我们在循环代码中添加 t.InOrder()，发现是删除最后一个值时崩溃的，因为此时 9 是根，循环里就直接走到删除的代码块中，去判断目标节点的左时，其中确定目标位置父亲的左还是右和目标位置的孩子关联时对空指针解引用，因为 parent 定义时是 nullptr。由此我们还发现了一种 parent 也是空的场景，先把根的左树全删除，再删除根，也会出现相同的问题。解决方法就是如果目标节点是根，也就是没有父亲，就让它的左或右作根。

✔ 修正

else

	//删除
	if(cur->_left == nullptr)//ab
	
		//没有父亲
		if(cur == _root)
		
			_root = cur->_right;//右作根
		
		else
		
			//确定目标位置父亲的左还是右和目标位置的孩子关联(目标位置的左右孩子在外层if已经确定了)
			if(cur == parent->_left)
			
				parent->_left = cur->_right;
			
			else
			
				parent->_right = cur->_right;	
			
		
		delete cur;
	
	else if(cur->_right == nullptr)//ac
	
		//没有父亲
		if(cur == _root)
		
			_root = cur->_left;
		
		else
		
			//确定目标位置父亲的左还是右和目标位置的孩子关联(目标位置的左右孩子在外层if已经确定了)
			if(cur == parent->_left)
			
				parent->_left = cur->_left;	
			
			else
			
				parent->_right = cur->_left;	
			
		
		delete cur;

6、InsertR

public:
	bool InsertR(const K& key)
	
		return _InsertR(_root, key);
	
private:
	bool _InsertR(Node* root, const K& key)
	
		if(root == nullptr)
		
			root = new Node(key);
			return true;
		
		else
		
			if(root->_key < key)
			
				return _InsertR(root->_right, key);	
			
			else if(root->_key > key)
			
				return _InsertR(root->_left, key);	
			
			else
			
				return false;

其实能用循环那就用循环，你可以认为递归大白话就是你少做一些事情，编译器多做一些事情，虽然使用递归代码量少了不少，但是却是编译器负重前行换来的，因为递归需要频繁的建立栈帧，且递归太深，有可能 stackoverflow，那么就得不偿失了，所以这里一般我们也不会实现递归版本，因为如果这棵树比较复杂，那么开销就会非常大，而这里依然要实现的原因是下面的引用用的很巧妙。
这里的 root 是一个局部变量，出了作用域就销毁了，所以需要在销毁前与它的父亲链接。这里找父亲的方式有很多种，比如可以多增加一个参数，每次递归把当前的 root 传给 rootParent，最后再比较链接；或者将参数 Node* root 改为 Node*& root，就已经插入成功了，因为如下图，目标位置是 9 的 _right 的别名，此时再 new 节点给 root，就直接跟 9 链接起来了，且第一次插入时 _root 为空，此时 root 就是 _root 的别名。

✔ 修正

public:
	bool InsertR(const K& key)
	
		return _InsertR(_root, key);
	
private:
	bool _InsertR(Node*& root, const K& key)
	
		if(root == nullptr)
		
			root = new Node(key);
			return true;
		
		else
		
			if(root->_key < key)
			
				return _InsertR(root->_right, key);	
			
			else if(root->_key > key)
			
				return _InsertR(root->_left, key);	
			
			else
			
				return false;

7、FindR

public:
	Node* FindR(const K& key)
	
		return _FindR(_root, key);
	
private:
	Node* _FindR(Node* root, const K& key)
	
		if(root == nullptr)
		
			return nullptr;
		
		if(root->_key < key)
		
			return _FindR(root->_right, key);	
		
		else if(root->_key > key)
		
			return _FindR(root->_left, key);
		
		else
		
			return root;

8、EraseR

public:
	bool EraseR(const K& key)
	
		return _EraseR(_root, key);	
	
private:
	bool _EraseR(Node*& root, const K& key)
		
		if(root == nullptr)
		
			return false;	
		
		else if(root->_key < key)
		
			return _EraseR(root->_right, key);
		
		else if(root->_left > key)
		
			return _EraseR(root->_left, key);	
		
		else
		
			//删除
			Node* del = root;
			if(root->_left == nullptr)//ab
			
				root = root->_right;
			
			else if(root->_right == nullptr)//ac
			
				root = root->_left;
			
			else//d
			
				//替代
				Node* minRight = root->_right;
				while(minRight->_left)
				
					minRight = minRight->_left;	
				
				root->_key = minRight->_key; 
				//大事化小,小事化了
				return _EraseR(root->_right, minRight->_key);
			
			delete del;
			return true;

可以看到这里递归的参数使用引用的方式，代码量少了很多，你甚至在情况 ab、ac 时只要找到目标节点，不用再判断目标节点父亲的左还是右。比如这里要删除 8，程序走到外层 else 时，这里的 root 不仅是 7 节点 _right 的别名，也是 8 节点的地址，7 节点 _right 的别名意味着 root 的改变就是 7 节点的 _right 的改变，8 节点的地址就意味着可以拿到 9 节点，它们并不矛盾，此时 root = root->_right 就可以完成链接。并且这里针对于先把 5 的左树删除再删除 5 的情况也能解决，解决点是套了一层 EraseR，root 是 _root 的别名，所以 root->_key == key，程序就走到 else，root 的左为空，root = root->_right，也就是 _root 的 _right 指向 7 节点。
对于 d 情况，引用就没用了，因为要找替代节点。但是还是能用点递归的，找到替代的节点替代后，现在要删除替代节点，想想递归的思想 “ 大事化小，小事化了 ”，比如要删除 5，替代完后就转换为以 7 节点为根删除 6。这里要明白的是转换为递归删除右子树的 minright，如果右子树越大，付出的代价就越大，同时这里二叉树进阶如果使用 C 语言来实现，那么这里就得传二级指针，它相对引用理解起来就费劲多了。

9、构造函数和析构函数和拷贝构造函数和赋值重载的实现

public:
	//BSTree() = default;//C++11
	BSTree()
		: _root(nullptr)
	
	~BSTree()
	
		_Destroy(_root);	
	
	//BSTree(const BSTree& t)
	BSTree(const BSTree<K>& t)
	
		_root = _Copy(t._root);
	
	//BSTree& operator=(BSTree& t)
	BSTree<K>& operator=(BSTree<K>& t)//现代写法 t1 = t2
	
		std::swap(_root, t._root);
		return *this;
	
private:
	Node* _Copy(Node* root)
	
		if(root = nullptr)
		
			return nullptr;	
		
		//深拷贝根
		Node* newRoot = new Node(root->_key);
		//递归拷贝左右子树
		newRoot->_left = _Copy(root->_left);
		newRoot->_right = _Copy(root->_right);
		//返回根
		return newRoot;
	
	void _Destroy(Node* root)
	
		if(root == nullptr)
		
			return;	
			
		//后序
		_Destroy以上是关于C++进阶：二叉树进阶二叉搜索树的操作和key模型key/value模型的实现 | 二叉搜索树的应用 | 二叉搜索树的性能分析的主要内容，如果未能解决你的问题，请参考以下文章 
 C++进阶：二叉树进阶二叉搜索树的操作和key模型key/value模型的实现 | 二叉搜索树的应用 | 二叉搜索树的性能分析
 C++进阶：二叉树进阶二叉搜索树的操作和key模型key/value模型的实现 | 二叉搜索树的应用 | 二叉搜索树的性能分析
 C++二叉树进阶（二叉搜索树,KV模型）
 C++二叉树进阶（二叉搜索树,KV模型）
 C++二叉树进阶
 二叉树进阶